Konec metabolické teorie?

Metabolická teorie biologie, vzniklá na přelomu století jakožto grandiózní pokus unifikovat porozumění biologickým procesům pomocí škálovacích vztahů v organismech, se začíná otřásat v základech. Zdá se, že intenzita metabolismu není tím, co řídí rychlosti všech biologických procesů, a že fundamentálnější budou nějaké hlubší zákonitosti růstu.

Když v roce 1997 vyšel v časopise Science článek [1] odvozující vztah mezi velikostí těla a rychlostí metabolismu organismů z geometrie transportních sítí uvnitř těla (viz rámeček), otevřel cestu k vybudování metabolické teorie biologie [2]. Ta tvrdí, že metabolismus jedinců je základem všech biologických procesů, jako jsou produkce biomasy, růst a množení, ale i cyklování živin či globální dynamika uhlíku, a že rychlost těchto procesů lze z rychlosti metabolismu přímo odvodit [3].

V prvním desetiletí 21. století to vskutku vypadalo, že konečně máme rigorózní nástroj kvantitativně propojující všechny procesy v biologii pomocí myšlenky, že metabolismus řídí vše. Hlavním argumentem bylo, že ze znalosti, jak rostou větvící se transportní sítě s velikostí těla, lze odvodit koeficient ¾, který charakterizuje nejen škálování rychlosti metabolismu (viz rámeček), ale i většiny ostatních procesů. Občas se sice objevovaly názory, že škálovací koeficient je ve skutečnosti variabilní nebo že odvození tříčtvrtinového koeficientu není matematicky úplně v pořádku, ale elegance a univerzalita teorie byly tak přitažlivé, že velká část biologické komunity ji plně přijala.

V minulé dekádě ovšem metabolická teorie utrpěla šrámy. Ukázalo se, že fraktální rozvodné sítě nejsou univerzální, že odvozovat z nich rychlost metabolismu tak úplně nejde a že v některých případech skutečně nepozorujeme kanonické škálování s tříčtvrtinovým koeficientem. Ještě horší ale bylo, že se tříčtvrtinový škálovací koeficient našel i v systémech, v nichž tyto fraktální rozvodné systémy nenajdeme – třeba v lidských společnostech či v zákonitostech růstu měst (Vesmír 95, 86, 2016/2).

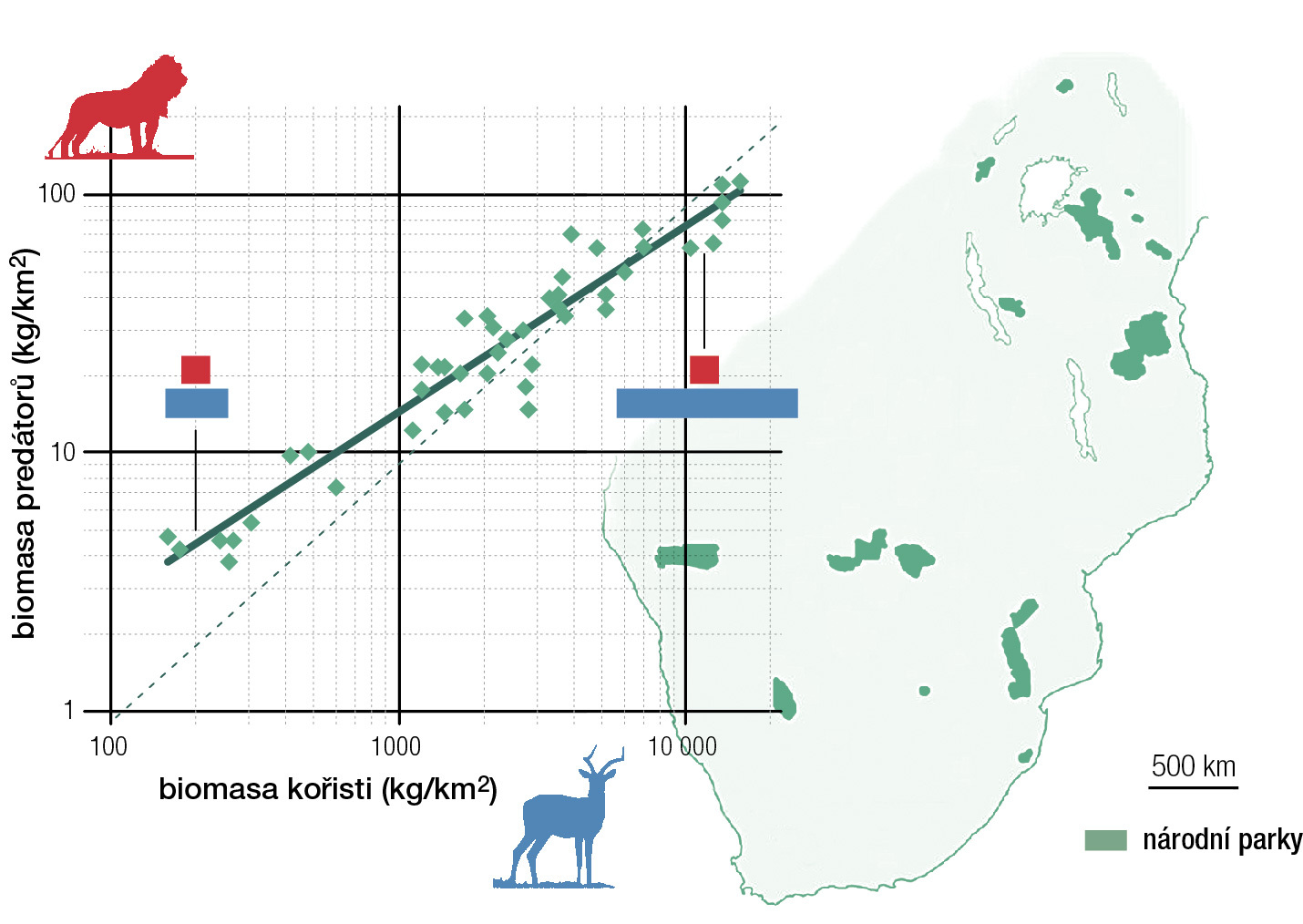
Asi nejkřiklavější příklad objevil Ian Hatton ve vztahu mezi celkovou biomasou herbivorů a biomasou všech jejich predátorů v afrických savanách, ale i v řadě dalších ekosystémů – když si proti sobě vyneseme biomasu kořisti a biomasu predátorů v logaritmickém měřítku, dostaneme přímku se sklonem ¾ (obr. 2). Podobný vztah najdeme i mezi biomasou a růstem (produkcí) biomasy – produkce biomasy v ekosystému také neroste s rostoucí biomasou proporčně, ale čím dál pomaleji. Ekosystémy s větším množstvím vegetace mají tedy relativně (vzhledem k celkové hmotnosti všech jedinců) nižší produkci biomasy primárních konzumentů, ale také relativně méně predátorů, kteří tuto nově narostlou biomasu odebírají. Metabolická teorie to nevysvětlí, poněvadž rozdíly v biomasách mezi různými ekosystémy nejsou dané rozdíly ve velikostech těl, ale čistě v počtech jedinců; žádné rozvodné sítě uvnitř těl organismů tam tedy nehrají roli.

Vztah mezi biomasou kořisti a biomasou predátorů v afrických savanách (jednotlivé body představují různé chráněné oblasti, kde byly počty velkých savců pravidelně monitorovány). Poměr biomas (ale i celkových počtů) predátorů a kořisti není konstantní (to by byl sklon přímky roven jedné, čemuž odpovídá přerušovaná čára), ale mění se systematicky podle gradientu produktivity – v nejsušších a nejméně produktivních územích je relativně vyšší proporce predátorů, ve vlhkém a produktivním prostředí je tomu naopak. Sklon přímky je velmi blízký ¾.

Když mi tyto záhadné vztahy Ian Hatton před lety ukazoval na konferenci věnované právě metabolické teorii, říkal jsem mu, že je bude velmi těžké publikovat, poněvadž nemají v rámci metabolické teorie žádné vysvětlení, přestože jsou zjevně robustní – není důvod, proč by třeba poměr počtu predátorů a kořisti měl klesat s rostoucím množstvím kořisti, navíc podle škálovacího vztahu, který byl odvozen jen pro vliv rostoucí velikosti těla. Kupodivu se mu to podařilo publikovat v Science [4], přestože v článku zcela bez obalu přiznal, že nemá žádné vysvětlení. Když pak Ian pobýval na podzim 2017 v CTS, dali jsme dohromady navazující projekt, spočívající v analýze celého spektra škálovacích vztahů mezi velikostí těla, početností, růstem, rychlostí množení a délkou života v rámci všech eukaryotních organismů. Výsledky vyšly loni v časopise PNAS [5] a myslíme si, že vrhají dost odlišné světlo na původ škálovacích vztahů.

Sloni jsou největší suchozemští živočichové a mají největší celkovou intenzitu metabolismu. Relativní intenzita vztažená na jednotku hmotnosti je u nich ale naopak nízká, čemuž odpovídá pomalá produkce potomstva – samice rodí slůně přibližně jednou za čtyři až pět let. Sloni plně dospívají kolem 18. roku a dožívají se 60–70 let. Dolní Zambezi, Zambie.Snímek Lenka Storchová

Priorita růstu

Ukázalo se, že metabolismus a velikost těla skutečně škálují s tříčtvrtinovým koeficientem, ale jen uvnitř hlavních skupin organismů, jako jsou savci, hmyz nebo (mnohobuněčné) rostliny. Když se ale podíváme na všechny eukaryotní organismy jako celek, rychlost metabolismu roste s velikostí těla v zásadě proporčně – dvakrát větší tvor má zkrátka v průměru dvakrát intenzivnější metabolismus, škálovací koeficient přes všechna eukaryota je tedy roven přibližně jedné.

To by ještě nebylo nic divného; odvození tříčtvrtinového koeficientu založené na geometrii rozvodných sítí může platit jen uvnitř jednotlivých skupin, přičemž ty skupiny se navzájem mohou lišit ještě v celkové hladině metabolismu (tedy v normalizační konstantě, viz rámeček), která je dána něčím dalším. Tím „něčím dalším“ může být omezení určující průměrný metabolický výkon jednotky „živé hmoty“ – kdyby tříčtvrtinový koeficient platil pro všechna eukaryota od nejmenších protist po plejtváka obrovského, znamenalo by to, že rychlost metabolismu na jednotku hmotnosti (viz rámeček) by byla pro protisty o mnoho řádů vyšší než pro onoho plejtváka. Zatímco malí jednobuněční tvorové by tedy prakticky hořeli, velcí tvorové by byli svým metabolismem blízko kusu ledu. Ani jedna z těchto možností není slučitelná se životem, takže vlastně není divu, že přes tolik velikostních řádů celková rychlost metabolismu roste přibližně lineárně s velikostí těla – průměrný metabolismus daného objemu živé hmoty zkrátka nemůže v takové míře kolísat.

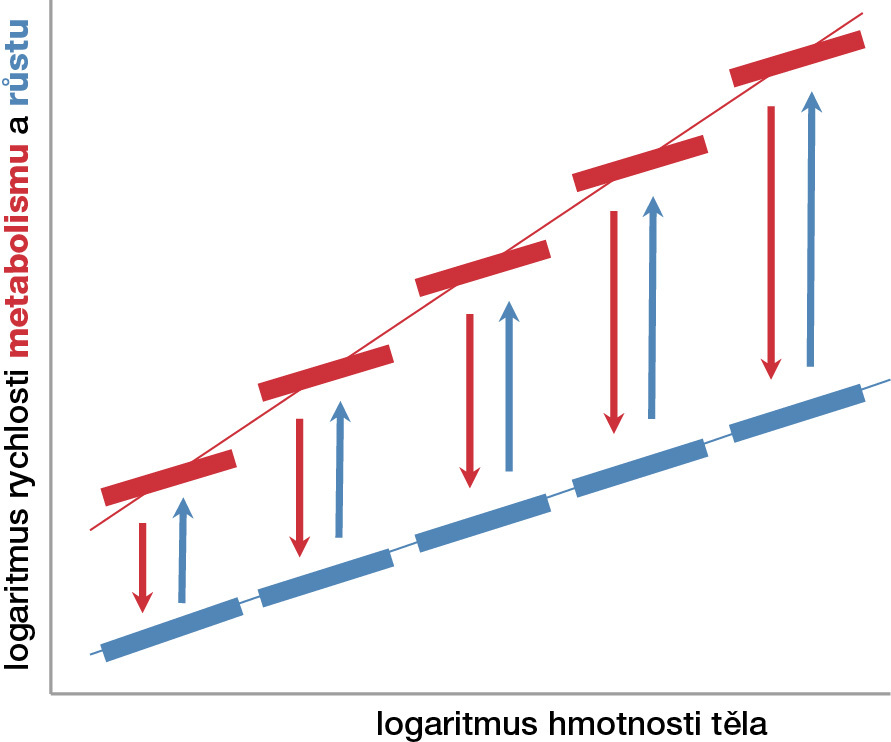
Zvláštní ale je, že toto se netýká škálování rychlosti růstu. K našemu velkému překvapení rychlost růstu (v zásadě přibývání biomasy za jednotku času, ať už jde o individuální růst, nebo produkci potomstva) škáluje se tříčtvrtinovým koeficientem jak v rámci jednotlivých skupin, tak přes všechny eukaryotní organismy. Škálování růstu je tedy univerzálnější než škálování metabolismu, což zpochybňuje centrální tezi metabolické teorie, že všechny biologické rychlosti plynou z omezení týkajících se rychlosti metabolismu. Kdyby tomu totiž tak bylo, těžko bychom vysvětlili, proč organismy všech skupin vykazují jeden univerzální škálovací vztah pro růst, když se jednotlivé skupiny liší v celkové rychlosti metabolismu (obr. 4).

Nabízí se tedy myšlenka, že rychlost růstu řídí nějaká zatím nepoznaná zákonitost, která je úplně univerzální, zatímco rychlost metabolismu je adjustovaná právě na určité škálování rychlosti růstu – a může se relativně volně měnit. Svědčí pro to několik dávno známých fenoménů. Přestože u savců škáluje klidový metabolismus s hmotností podle tříčtvrtinového koeficientu, aktivní metabolismus (v době maxima aktivity) nebo naopak metabolismus v době hibernace rostou s hmotností prakticky proporčně (škálovací koeficient je blízký jedné), takže jej disproporčně se zvětšující fraktální rozvodné sítě asi zase tak příliš neomezují. Fenomén „kompenzačního růstu“ (urychlení růstu po jeho umělém zpomalení, takže nakonec „dostihne“ standardní růstovou křivku) zase ukazuje, že metabolismem není růst organismu striktně omezen. Takže to vypadá, že rychlost metabolismu se uzpůsobuje požadavkům růstu, a ne naopak.

Původ škálovacích vztahů

Zatím ovšem nikdo nepřišel s vysvětlením, proč by růst měl vykazovat univerzální škálovací vztahy charakterizované tříčtvrtinovým koeficientem (když to tedy nesouvisí s metabolismem). Ian sice spekuluje o vlastnostech biologického růstu, který spočívá jednak v prostém zvětšování objemu, jednak v replikaci základních jednotek (buněk, jedinců, rodinných skupin…), ale zatím nic z toho není podložené řádnými matematickými argumenty, které by vedly k tříčtvrtinovému koeficientu. Problém je v tom, že tento koeficient (a z něj odvozený koeficient –1/4) se vyskytuje v tak odlišných systémech, že vysvětlení musí spočívat v něčem zcela obecném, co jde mimo biologii jednotlivých skupin organismů a jednotlivých ekosystémů.

Schematické znázornění škálování metabolismu (červeně) a růstu (čili produkce biomasy; modře) v rámci jednotlivých skupin (jako jsou savci, hmyz nebo cévnaté rostliny; silné krátké čáry, jejichž sklon je ve všech případech přibližně ¾) a přes všechna eukaryota (tenké čáry; tady se liší sklon škálování metabolismu, který je blízký jedné). Šipky pak značí možné směry kauzality – buď rychlost metabolismu podmiňuje rychlost růstu (červeně), nebo naopak (modře). Pokud ale kauzalita vede od metabolismu k růstu, těžko vysvětlíme, proč škálovací vztah přes všechna eukaryota leží na jedné přímce se stejným (tříčtvrtinovým) sklonem, jako mají jednotlivé skupiny, když pro metabolismus to neplatí (znamenalo by to mimo jiné, že z nějakého důvodu je na růst dislokována s rostoucí hmotností stále menší proporce energie). Opačný směr kauzality dává lepší smysl, poněvadž škálování v rámci jednotlivých skupin vysvětlíme adjustací intenzity metabolismu pro potřeby růstu, zatímco škálování napříč eukaryoty může být způsobeno omezením rychlosti metabolismu pro jednotku živé hmoty.

Metabolická teorie předpokládá univerzální škálování transportních sítí uvnitř těla se změnou velikosti těla. Ale tvary organismů a způsob jejich růstu jsou velmi variabilní, takže předpoklad, že transportní systémy jsou v principu stejné u savců jako třeba u této tropické mnohonožky, je přinejmenším diskutabilní. Zambie.Snímek Petr Pokorný

Už v roce 2008 upozorňovali Lev Ginzburg a John Damuth [6], že tříčtvrtinový koeficient může ve skutečnosti souviset s dimenzionalitou našeho světa, třemi rozměry prostorovými a jedním časovým, ale ani oni nepředložili matematicky rigorózní teorii. Upozornili však na jednu důležitou věc, totiž že možná děláme chybu, když se něco (třeba škálování metabolismu nebo růstu) snažíme odvodit z vlastností něčeho jiného (třeba z velikosti těla a souvisejících omezení). Zapomínáme totiž, že úplně všechno je produktem evoluce, čili například ani velikost těla není něco neměnného a základního, co by nutně určovalo vše ostatní. Možná jde spíš o to, které kombinace vlastností dlouhodobě přežívají, než o to, co je příčinou čeho.

Ilustrujme si to myšlenkovým experimentem. Jak by živý svět vypadal, kdyby metabolismus i růst škálovaly s velikostí těla proporčně tedy s koeficientem rovným jedné? Vše by se zjednodušilo, jen by nastala jedna podivnost: počet potomků za jednotku času by nezávisel na velikosti těla (poněvadž ten je proporční produkci biomasy vztažené k jednotce hmotnosti), a tudíž i mortalita a doba dožití by musely být stejné pro organismy všech velikostí. Slon by žil nejen stejně dlouho jako myš, ale i stejně dlouho jako jednobuněčná měňavka. To zjevně nedává smysl; existuje řada pádných důvodů, proč větší organismy žijí déle než ty menší, a o to pomaleji se rozmnožují.

Je proto možné, že škálovací vztahy vyjadřují spíše než co jiného jakousi harmonii mezi různými vztahy, tedy jediné možné uspořádání, kdy různé procesy jsou dlouhodobě v rovnováze a vzájemném souladu. Proč by to ale vedlo právě ke tříčtvrtinovému škálovacímu koeficientu, to zatím netušíme. Třeba na něco přijdou čtenáři Vesmíru.