Relativistický čas – čas našeho světa
| 6. 5. 2024„Někteří filozofové … se domnívají, že fyzika není schopna popsat nejzákladnější aspekty reality, a zavrhují ji proto jako zavádějící formu poznání. V minulosti se však už mnohokrát prokázalo, že nepřesná je naopak naše intuice: kdybychom u ní setrvali, pořád bychom ještě věřili, že Země je placatá a že Slunce obíhá kolem ní. Naše intuice se vyvinula z našich omezených zkušeností.“
Carlo Rovelli, 7 krátkých přednášek z fyziky, Dokořán, s. 72
Jedním ze zásadních přínosů fyziky 20. století bylo přesnější pochopení vlastností času. Tyto poznatky jsou zformulované v teorii relativity. Pokusme se připomenout si, v čem se liší od zažitých představ.
Klasická fyzika reflektující naši tisíciletou zkušenost říká, že existuje globální současnost, jednoznačně určující prostor v jednom okamžiku, a že existuje univerzální čas, který takové současnosti čísluje a který běží pro všechny stejně. Univerzální čas vstupuje do fyzikálních zákonů popisujících pohyby těles a vývoj složitějších systémů.
1. Prostoročas
Prostoročas je soubor všech událostí, které se kdy odehrály a kdy odehrají. Událost je bod s určeným časovým výskytem, tady a teď. Matematicky je prostoročas čtyřdimenzionální prostor – tři dimenze odpovídají prostorovým rozměrům a čtvrtá časovému směru.
Vedle událostí do prostoročasu umísťujeme i složitější útvary. Uvažujme například historii částice. Historií máme na mysli celý její časový vývoj. Ten si můžeme představit jako posloupnost událostí, ve kterých se částice vyskytovala – což lze geometricky reprezentovat jako křivku v prostoročase. V relativitě takovým křivkám říkáme světočáry.
Prostoročas si můžeme představovat jako historii celého vesmíru. Neznamená to však, že bychom historii vesmíru museli chápat jako dokončenou a hotovou. Spíše si představujme prostoročas jako mapu, do které si historii našeho světa zaznamenáváme.
Tuto intuici jsme získali zkoumáním světa na pozemských časových a prostorových škálách zahrnujících malé rychlosti. Když jsme však obrátili pozornost na situace, ve kterých hrají roli obrovské rychlosti či velké rozměry (např. zkoumání elementárních částic v urychlovačích či pozorování vesmíru), zjistili jsme, že tato intuice v našem světě nefunguje. Že čas našeho světa je složitější. Neexistuje globální současnost a neexistuje jeden univerzální čas běžící pro všechny stejně.
Nové, přesnější porozumění času formuluje teorie relativity jako vlastnosti prostoročasu. Ty nejdůležitější jsou:
- kauzální struktura,
- metrická struktura,
- inerciální struktura.
Kauzální struktura nahrazuje pojem současnosti. Metrická struktura nám umožňuje měřit individuální čas každého systému. Inerciální struktura definuje inerciální soustavy.
Tyto struktury nejsou nezávislé, ale úzce provázané. Avšak každá z nich je spojena se samostatným fyzikálním fenoménem. Ikonicky je můžeme představit jako:
- maximální rychlost šíření signálu,
- vlastní čas závisející na pohybu,
- význačnost volných pozorovatelů.
První dva fenomény překračují naši běžnou intuici. Naproti tomu volní pozorovatelé hrají klíčovou roli již při budování inerciálních soustav v klasické fyzice a jejich role zůstává přibližně stejná. Zaměřme se proto na první dva fenomény.
Kauzální struktura
První netriviální fakt měnící naše chápání kauzality je existence omezení na rychlost šíření signálu. Nemáme k dispozici libovolně rychlý signál, ke každému signálu nelze najít ještě rychlejší. Naopak existuje nejrychlejší možný signál, jehož rychlost je konečná.
Existence omezení na rychlost signálu nabourává náš jednoduchý koncept kauzality založený na globální současnosti. Běžně rozumíme, že dvě události jsou současné, pokud z jedné do druhé můžeme poslat „nekonečně rychlý“ signál. Pokud můžeme druhou událost okamžitě informovat o té první. Jestliže jsou ale signály rychlostně omezené, takto jednoduše současnost definovat nelze.
Kauzální vztahy však nadále definujeme podle toho, zda se jednotlivé události mohou ovlivňovat. Můžeme definovat kauzální minulost a budoucnost zvolené události. Zvolme si konkrétní místo a okamžik, ve kterých se nacházíme. Kauzální minulostí této události nazveme všechny události, o kterých bychom se mohli dozvědět. To znamená, ze kterých k nám stihne dorazit fyzikální signál. Naopak kauzální budoucností naší události nazveme všechny události, které můžeme ovlivnit, ke kterým můžeme poslat signál my.
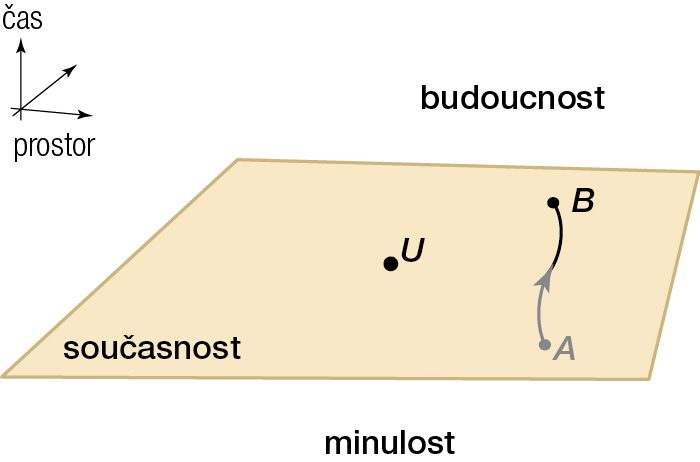
V běžné představě klasické fyziky by kauzální minulost a kauzální budoucnost vyplnily v podstatě celý prostoročas, byly by odděleny pouze tenoučkou vrstvou současnosti (obr. 1). V našem reálném světě tomu tak není. Omezení na rychlost šíření signálu způsobí, že zbude mnoho událostí, které nejsou vůči nám ani v minulosti, ani v budoucnosti (viz obr. 2). Tyto události jsou od nás příliš daleko. Žádný signál k nám od nich nestačí doletět. A stejně tak žádný signál, který vyšleme, nestihne dorazit k nim.
Tyto události netvoří jenom tenkou vrstvičku. Naopak zahrnují celé dlouhé časové úseky po sobě jdoucích událostí. Tyto „ne-minulé“ a „ne-budoucí“ události tak nemůžeme nazvat všechny současné s naší událostí. Bylo by podivné nazývat současnými událostmi ty, které se staly po sobě. Teorie relativity tak pro ně zavádí nové slovo, nazýváme je prostorupodobné k naší události.
Pojmy kauzální minulosti, kauzální budoucnosti a prostorupodobnosti jsou vztažené ke konkrétní události. Každá událost má svoji budoucnost a minulost. Rozdělení na minulost a budoucnost je tak daleko individuálnější, jemnější.
Problémy se současností
V této kauzální klasifikaci nám nakonec zcela proklouzl pojem současnosti. Současnost nejsme schopni definovat pomocí kauzálních vztahů. Kauzalita, říkající, které události se mohou navzájem ovlivňovat, nevymezí dostatečně přesně pojem současnosti. V našem světě bohužel nic jako univerzální současnost neexistuje.
Nelze například jednoznačně říci, které události jsou současné na Alfa Centauri s okamžikem, kdy čteme tento text. Na Alfě Centauri bude existovat zhruba devítiletý úsek mezi posledním okamžikem, ze kterého nás mohli kontaktovat a zrazovat nás od čtení textu, a prvním okamžikem, kdy se mohou dozvědět, že jsme text přečetli. Všechny události v tomto úseku jsou kandidáty na současnost s naším rozjímáním nad kauzalitou. Ale nelze nijak vybrat, která z těchto událostí je s námi doopravdy současná.
Nabízelo by se, že ta opravdu současná událost je ta „prostřední“, ta v polovině devítiletého úseku. Vskutku, takto bychom mohli zavést jistý pojem současnosti. Tato konstrukce však závisí na volbě pozorovatele (v našem případě Alfacentauřana), který monitoruje poslední okamžik, kdy k nám mohl odeslat zprávu, a první událost, kdy může dostat odpověď.
3. Souřadnicová současnost
Přestože kauzální struktura nevymezuje jednu univerzální současnost, lze zavést současnost spojenou s inerciální soustavou. Taková současnost ale bude pro navzájem se pohybující soustavy různá.
Jako analogii si můžeme uvést pojmy vertikálního a horizontálního směru v euklidovském prostoru. V prázdném euklidovském prostoru tyto pojmy nemají univerzální význam. Euklidovský prostor je izotropní a žádný směr není preferovaný.
Můžeme však zvolit vztažnou soustavu, která nám vertikální a horizontální směry vybere. Typicky zvolíme přímku, kterou prohlásíme za vertikální osu. Horizontální roviny definujeme jako roviny kolmé na vertikální směr. Je ale jasné, že můžeme zvolit různé soustavy s různými vertikálními směry.
Podobně v prostoročase: světočára inerciálního pozorovatele odpovídá volbě vertikálního směru a roviny „kolmé“ na tuto světočáru definují souřadnicové současnosti. Teorie relativity dává konkrétní předpis, co znamená „kolmost“ v prostoročasovém smyslu. Tento předpis odpovídá volbě „prostřední události“ zmiňované v textu.
Ukazuje se, že jiný pozorovatel, který se vůči systému Alfa Centauri pohybuje, identifikuje jako „prostřední událost“ jinou událost. Pokud si takový pozorovatel zavede svoji současnost, bude se různit od té zavedené na Alfa Centauri.
Těmto současnostem se říká souřadnicové současnosti či současnosti inerciální soustavy. Jde o užitečný pojem, ale není jednoznačný. Inerciální soustavy, které se vůči sobě pohybují, mají tyto současnosti různé.
4. Výpočet vlastního času
Pokud popíšeme světočáru vzhledem k inerciální soustavě, pro časovou délku lze používat časově modifikovanou Pythagorovu větu. Prostoročasová úsečka, jejíž koncové body mají rozdíl souřadnic Δt, Δx, Δy, Δz, má časovou délku Δt danou rovnicí
–c2Δτ2 = –c2Δt2 + Δx2 + Δy2 + Δz2.
Časové trvání zakřivené světočáry získáme podobně jako při počítání délek křivek: světočára se rozseká na posloupnost krátkých úseků, které již lze považovat za úsečky. Pro ty použijeme modifikovanou Pythagorovu větu a vše sečteme.
Vlastní čas
Druhým netriviálním faktem týkajícím se času je, že čas není univerzální, pro všechny stejný. Čas relevantní pro fyzikální procesy totiž závisí na konkrétním pohybu systému v prostoročase. Podél každé světočáry – ať už tělesa, pozorovatele, či laboratoře – můžeme definovat tzv. vlastní čas, čas, který určuje vývoj jevů v blízkosti světočáry. Jedná se o čas, který bude vstupovat do fyzikálních zákonů popisujících tyto jevy. Čas určující kmitání pružinky, kývání kyvadla, oscilaci atomu či biologické procesy, včetně stárnutí organismů a člověka.
Pokud budeme mít dva pozorovatele stojící vedle sebe, vlastní čas jim běží stejně. Budou-li se však vůči sobě pohybovat, vlastní čas bude pro každého z nich individuální.
Dva pozorovatelé, kteří se rozejdou a pohybují se po různých drahách různými rychlostmi, poté, co se znovu setkají, zjistí, že „nažili“ jiné množství času. Že jim uplynulo různé množství jejich vlastního času. Neexistuje nějaký společný čas, ve kterém by stárli stejným způsobem. Každý z nich stárne podle individuálního vlastního času (viz rámeček 5).
5. Paradox dvojčat
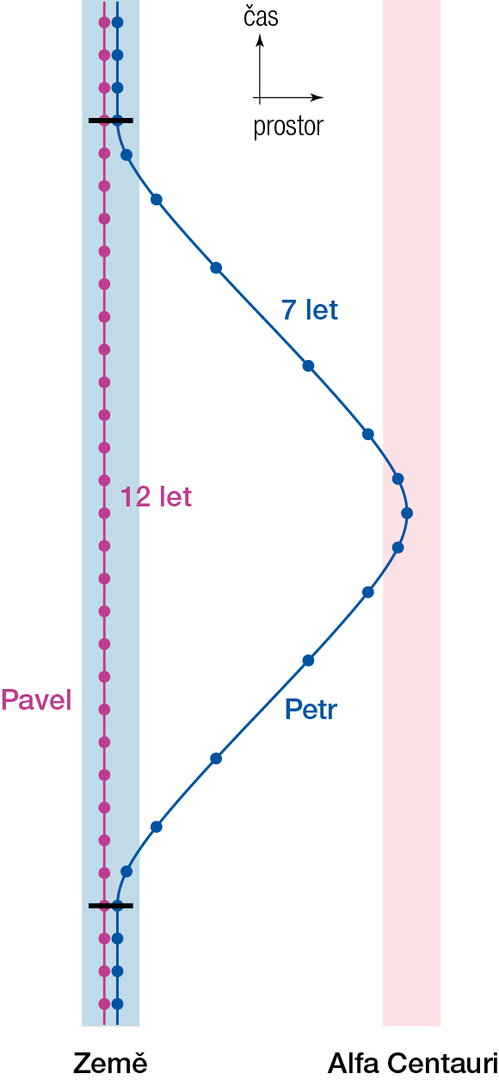
Fenomén individuálního vlastního času se často popularizuje na příkladu dvojčat Petra a Pavla. Petr vyrazí v kosmické lodi na výlet k blízké hvězdě a zpět, kdežto Pavel zůstane na Zemi. Zajímá nás, o kolik oba zestárli mezi okamžikem rozchodu a opětovného shledání. Skutečností našeho světa je, že nezestárnou stejně!
Petr bude po svém návratu mladší. Pokud se pohyboval během své cesty dostatečně rychle, může být oproti Pavlovi mladší velmi výrazně. Pavel, který zůstal na Zemi, se totiž pohybuje přibližně po přímé světočáře (na mezihvězdných škálách, které zde hrají roli, je tato aproximace velmi dobrá). Jeho světočára je tak časově nejdelší.
Situace přitom není symetrická. Světočára Petra je netriviálně zakřivená, kdežto Pavlova světočára je přibližně rovná. Tento rozdíl určuje různou dobu, o kterou oba zestárnou (viz obr. 3).
Paradox dvojčat se nazývá paradoxem, protože v době, kdy byl formulován (P. Langevinem v r. 1911), tento příklad poprvé populárně odhaloval individuálnost vlastního času. Samotná možnost, že by uběhlý čas mohl být pro různé pozorovatele různý, zněla tehdy pro mnohé zcela paradoxně.
Dalším důvodem pro užívání slova paradox byl argument, že podle principu relativity by vztah Petra a Pavla měl být ekvivalentní. Proto by jeden neměl zestárnout víc než druhý. Zde se však jedná o chybné použití principu relativity. Pozorovatelé Petr a Pavel nejsou ekvivalentní, protože Pavlova světočára je přibližně přímá, a Petrova ne.
Paradox dvojčat tak není skutečným logickým paradoxem, ale pouze zažitý název pro velmi důležitý fenomén našeho světa.
Tato skutečnost uniká naší každodenní pozornosti, protože při běžných rychlostech jsou rozdíly v „nažitých“ časech řádu nanosekund, a tedy nepozorované. Tyto rozdíly se významně projeví, až když do hry vstupují rychlosti srovnatelné s rychlostí světla.
Vlastní čas lze chápat jako jakousi časovou délku světočáry. Při tomto porozumění nás už tolik nepřekvapí, že časová délka závisí na konkrétní světočáře. A teorie relativity nám dává předpis, jak tuto délku spočítat (viz rámeček 4).
V euklidovské geometrii platí, že nejkratší křivka spojující dva body je úsečka. Podobně se můžeme ptát, jak v prostoročase souvisejí časové délky různých světočar spojujících dvě události. Kolik vlastního času uběhne podél těchto světočar?
Ukazuje se, že přímá světočára spojující obě události je opět výjimečná. Na rozdíl od euklidovské geometrie však trvání přímé světočáry je to nejdelší! Pozorovatel pohybující se po přímé světočáře „nažije“ nejvíce času. Zestárne více než jakýkoli jiný pozorovatel pohybující se mezi stejnými dvěma událostmi (viz obr. 3 a rámeček 6).
A který pozorovatel se pohybuje po přímé světočáře? Ten, jenž se pohybuje bez zrychlení. Pozorovatel, na kterého nepůsobí žádná výsledná síla – volný pozorovatel.
Nejméně času naopak nažijí pozorovatelé, kteří se pohybují rychlostí velmi blízkou maximálnímu signálu. Pokud se celou dobu budou pohybovat skoro rychlostí světla, mohou zestárnout o v podstatě libovolně krátký čas.
Relativistický běh času
Náš prostoročas tak nemůžeme chápat jako jednolitě se odvíjející běh globálního času posunující jednotnou současnost z minulosti do budoucnosti.
Správná představa je prostoročas obsahující světočáry jednotlivých pozorovatelů. Každý takový pozorovatel stárne podle svého času, který závisí na tvaru jeho světočáry.
Pro každého pozorovatele si můžeme představovat, jak se jeho individuální přítomnost posouvá podél jeho světočáry (viz obr. 4). Vzhledem k této přítomnosti můžeme pak určit kauzální minulost pozorovatele v daný okamžik. Různí pozorovatelé mají svoji vlastní přítomnost. Proto i jinak chápou, co je jejich kauzální minulost.
Vidíme, že struktura času v našem světě je složitější, než nabízí naše běžná zkušenost. Díky teorii relativity jí však dobře rozumíme a umíme ji používat při zkoumání fyzikálních zákonů.
Ke stažení
 článek ve formátu pdf [630,67 kB]
článek ve formátu pdf [630,67 kB]
O autorovi
Pavel Krtouš