Hledání vzorců v mapě

Zajímavé informace o jevu, kterým se zabýváme, můžeme získat jeho zobrazením v mapě. Můžeme zkoumat jeho rozložení v prostoru či vztah k jiným skutečnostem. Například při sledování nezaměstnanosti můžeme zjišťovat, kde je nejvyšší a jestli mají tyto oblasti něco společného. Přírodovědci mohou naopak porovnávat výskyt druhů v průběhu času a ekologové stupeň znečištění prostředí v různých lokalitách. V mapě můžeme porovnávat místa pozorování, nacházet shluky podobných hodnot a hledat v nich zákonitosti a prostorové vzorce, které nám pomohou dotyčné jevy pochopit, rozpoznat jejich příčiny, a předvídat budoucí vývoj.

Ale prosté zakreslení jevu do mapy nemusí vždy stačit. Pokud se rozhodneme zobrazit každý výskyt jednou značkou (například kolečkem), značky se mohou začít překrývat, takže v mapě nebude rozdíl mezi místem s jedním a deseti výskyty. To je chvíle pro sofistikovanější metody vizualizace a pro statistickou analýzu v prostoru.

Otázka blízkosti

Prostorová analýza má mnoho podob. Někdy při ní bereme v úvahu pouze souřadnice x a y, někdy nás zajímá vzdálenost mezi jevy, jindy zase jejich tvar a orientace. I prostorová data můžeme zkoumat tradičními statistickými metodami, ale měli bychom si uvědomit, že ty obvykle uvažují data jako nezávislá, zatímco prostorový přístup vychází z tzv. prvního zákona geografie (Toblerova zákona), který zní: „Blízké jevy spolu souvisejí více než jevy vzdálené.“

Proto si nejprve musíme odpovědět na otázku: „Co v našem případě považujeme za blízkost?“ Definice blízkého okolí je důležitá z několika hledisek. Určuje totiž měřítko, ve kterém hledáme podrobnosti a rozdíly. Určuje také množství prvků, se kterými prvek porovnáváme, a definuje rovněž i způsob, jakým převádíme skutečný jev do abstrakce výpočtů.

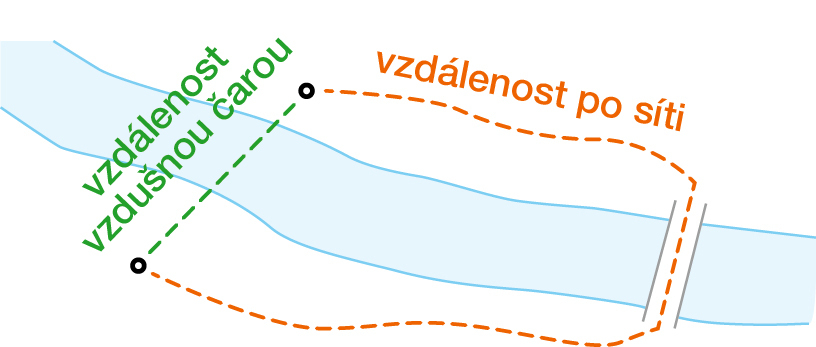
Nejsnazší definice okolí je vzdálenost vzdušnou čarou. Jenže dva břehy řeky jsou od sebe jen kousek, zatímco pro zvířata může cesta na druhý břeh znamenat celodenní výpravu, než dorazí na místo, kde je tok řeky možné překonat. Pro tyto případy je vhodnější uvažovat vzdálenost po síti, tedy délky skutečných spojnic mezi dvěma místy, ať to jsou stezky pro zvěř, nebo silniční síť pro automobily (obr. 1).

Vzdálenost nemusí být vždy vhodné měřit vzdušnou čarou.

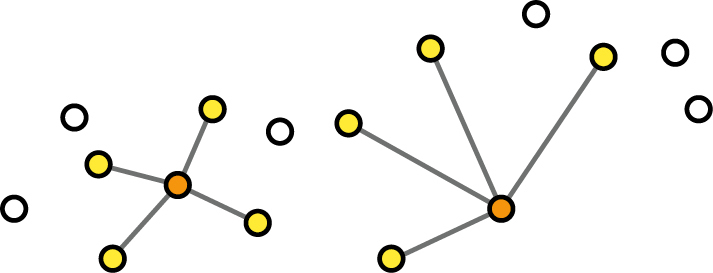
Okolí nemusíme definovat limitem vzdálenosti. Můžeme určit, že za okolí každého bodu budeme pokládat čtyři nejbližší ostatní body (obr. 2). Tak je zajištěno, že každý bod bude mít ve svém okolí nějaké sousedy, a navíc jich bude vždy stejný počet. Velikost tohoto sousedství je však pro každý prvek jiná. V oblastech řídkého výskytu budou větší a v místech hustého výskytu menší.

Definice blízkosti počtem nejbližších sousedů.

Otázka měřítka

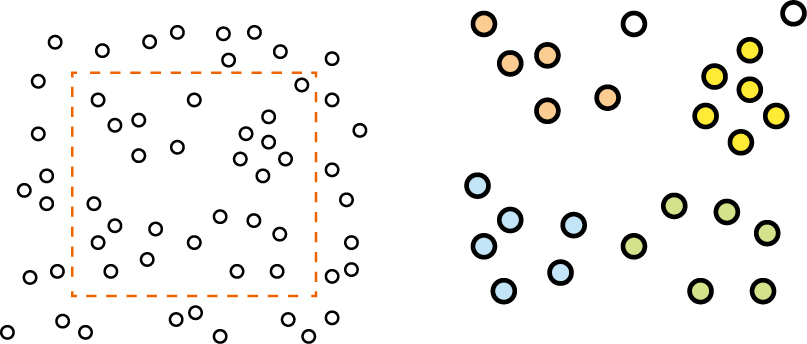
Hledáme-li shluky bodů, musíme určit měřítko, ve kterém pracujeme. To se řídí charakterem dat. Pokud analyzujeme data dopravních nehod, nejspíše budeme hledat shluky o velikostech křižovatky. Pokud chceme nalézt místa, kam často udeří blesk, budeme pracovat spíše v kilometrech. Špatně zvolené měřítko nám buď všechna data nahustí do několika málo shluků, nebo je naopak rozpustí v prostoru a shluk nenajdeme žádný (obr. 3).

Agregace bodů do ploch Pokud nás zajímá četnost výskytu jevu v území, je vhodné je agregovat do plošných areálů. Ty mohou být tvořeny pravidelnou čtvercovou nebo šestiúhelníkovou sítí, ale použít můžeme i jakoukoliv jinou sadu hranic, například hranice obcí, okresů nebo států. Pozor si však musíme dát na tzv. problém měnitelné plošné jednotky, který upozorňuje na to, že použití geografických hranic může ovlivnit výsledky, protože hranice jsou vůči datům voleny náhodně, nikoliv však neutrálně.

Z dálky se mohou body jevit jako homogenní skupina, v podrobnějším měřítku ale začneme identifikovat shluky.

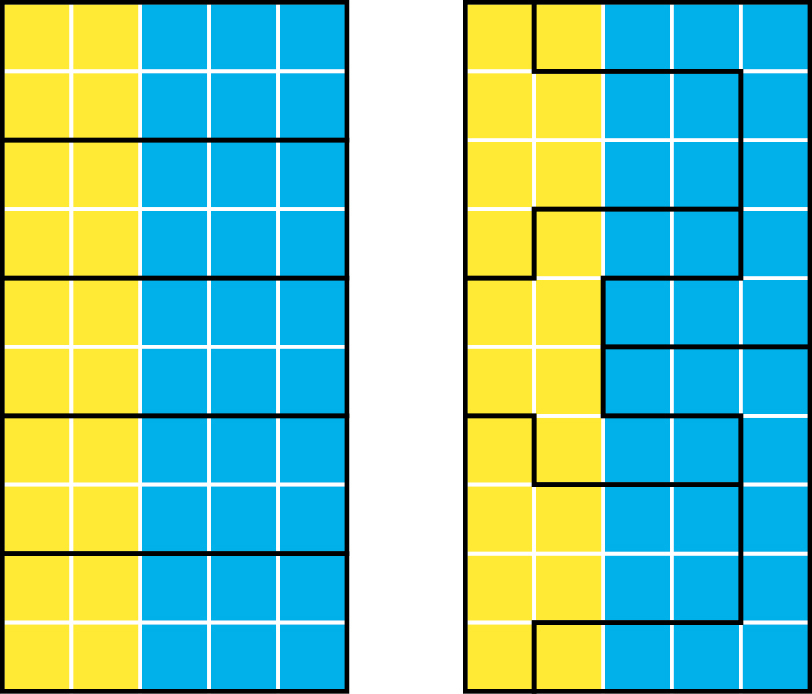
To se odráží například i v účelové manipulaci s hranicemi volebních okrsků, problému, který se aktuálně řeší zejména v USA. Princip tohoto jevu, pojmenovaného po historickém guvernéru Elbridgeovi Gerrym „gerrymandering“, spočívá v důvtipné manipulaci s hranicemi volebních obvodů. Lze pomocí ní docílit, aby strana A získala většinu hlasů ve většině volebních okrsků, přestože strana B má na celém území v součtu více hlasů (obr. 4). Při práci si proto musíme dát pozor, zda naše volba areálů nevnáší do prováděné analýzy chybu.

Gerrymandering. V původní konfiguraci volebních okrsků vyhrávají modří ve všech pěti okrscích. Vhodnou volbou hranic nových okrsků můžeme skóre otočit na 3 : 2 ve prospěch žlutých. Pokud záleží pouze na celkovém výsledku, žlutí dokonce vyhrají celý obvod, ačkoliv jich je jen 40 %.

Zdroj: podle Wikipedie

Statistické metody

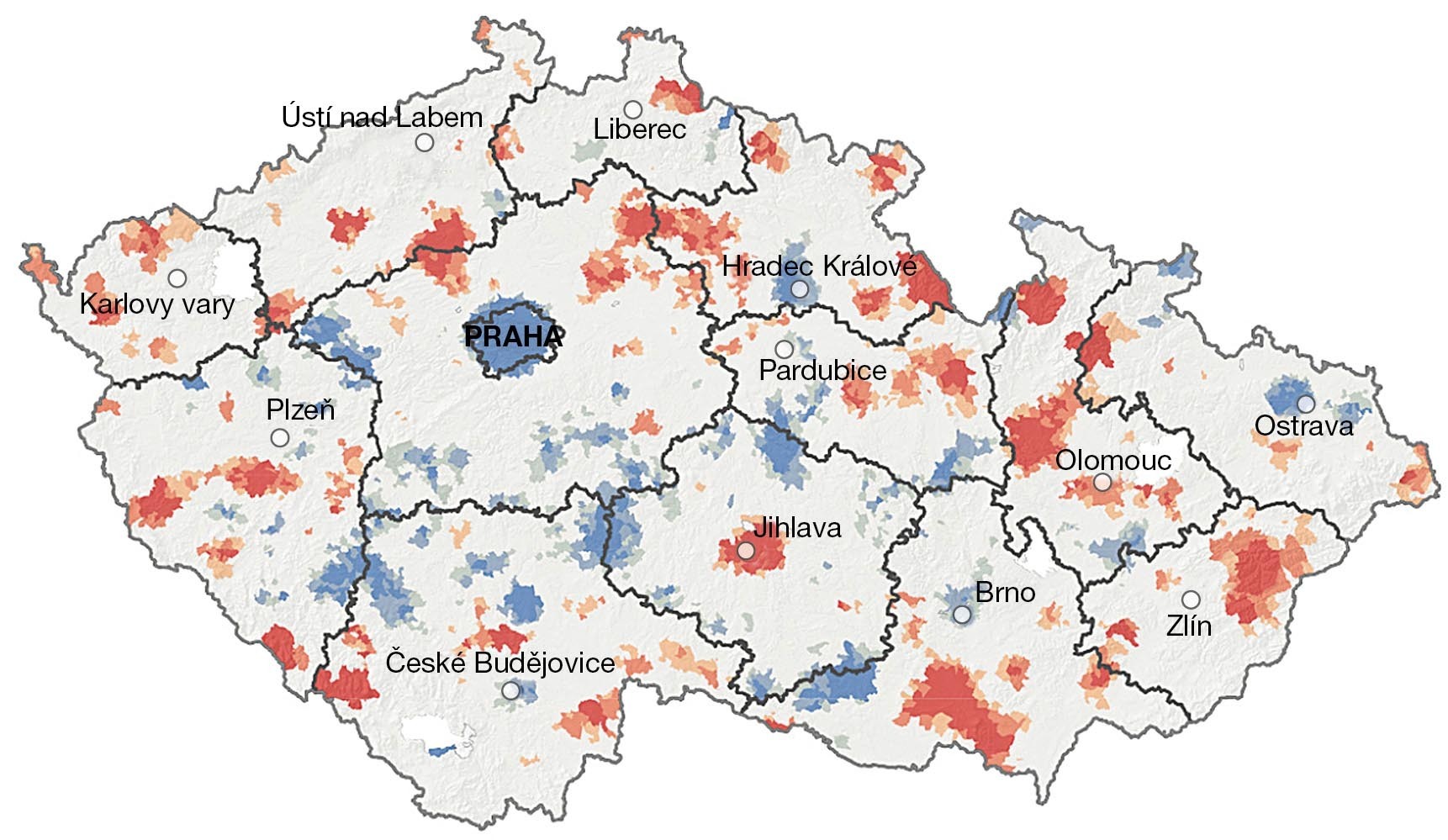
Agregace do polygonů nám vyřešila úvodní problém s body nepřehledně naskládanými na sebe. Polygony v sobě mají údaj, kolik bodů obsahují, a my můžeme celou mapu obarvit na základě tohoto atributu. Můžeme si vybrat barevnou škálu – například modrou pro nejnižší výskyty, která postupně přejde do žluté pro nejvyšší hodnoty – ale než tak uděláme, musíme si uvědomit, že rozhodnutí o tom, kam umístíme hranice jednotlivých barevných intervalů, bychom neměli stanovit pouze podle našeho úsudku, ale použít pro to způsob, který má buď opodstatnění v metodologii výzkumu, nebo ve statistice. Existuje například metoda přirozených zlomů (Jenksova optimalizace), která hranice intervalů určí na základě rozdělení dat.

Dalším způsobem je analýza hot-spot, která vyhledá statisticky významná místa s výskytem vysokých a nízkých hodnot. Algoritmus vezme prvek a jeho okolí a zeptá se: „Jsou hodnoty v tomto okolí významně odlišné od hodnot v celé sledované oblasti?“ Pokud jsou vyšší, je prvek identifikován jako „horká skvrna“, hot spot; nižší jako cold spot. Tento proces probíhá na základě statistických veličin, jako je p-hodnota a z-skóre. Tak je možné z různorodých dat získat poměřitelné a statisticky podložené podklady (obr. 5).

hot-spot Analýza změny volební účasti sněmovních voleb 2021 oproti volbám 2017. Modrá barva: statisticky významný pokles účasti. Červená barva: statisticky významný nárůst.

Zdroj: Co rozhodlo volby? Jakub Lysek a Tomáš Lebeda, Univerzita Palackého, Jan Souček a Lucie Patková, ARCDATA PRAHA; www.arcdata.cz/volby2021

Časové kostky a geografická regrese

Časoprostorová kostka umožní zkoumat změny jevu i v průběhu času.

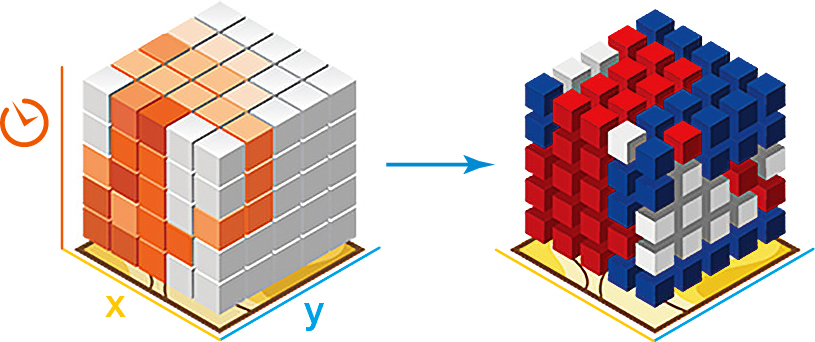
Analýza hot-spot může být při zkoumání prostorových dat teprve začátek. Máme-li data nasbíraná v různých obdobích, můžeme zkoumat jejich vývoj v čase a místo mapy vytvořit tzv. časoprostorovou kostku – soubor hot-spot analýz naskládaných na sebe (obr. 6). Změny v ní můžeme zkoumat nejen v kontextu geografické, ale také temporální blízkosti a dobře v ní identifikujeme rovněž periodické změny.

Lineární regrese metodou nejmenších čtverců je široce známá statistická metoda. Geografická regresní analýza je založena na stejném principu, bere však v úvahu první zákon geografie a uvažuje také vzdálenost mezi jednotlivými prvky. Tradiční regrese vytváří jednu rovnici na základě všech prvků v souboru. Geografická regrese je ale lokální a vytváří pro každý prvek specifickou rovnici, ve které se vliv ostatních prvků zmenšuje s jejich vzdáleností – zde opět přichází ke slovu námi definované okolí.

Díky geografické regresi můžeme zkoumat jevy mnohem komplexněji, v závislosti na jejich rozmístění v území. A pokud se nám na základě těchto metod podaří identifikovat proměnné, které zkoumaný jev ovlivňují, dokážeme i modelovat jeho budoucí vývoj. Využití prostorové statistiky tak do analýzy přináší doslova nový rozměr.