Origamová geometrie

Příběh, který budu vyprávět na pokračování, je neobyčejným příběhem o té nejobyčejnější geometrii. V té se začíná s pravítkem a kružítkem a ukazuje se, kolik se toho těmito jednoduchými nástroji dá udělat (zkonstruovat). Něco se ale nedaří a nedaří, například rozdělit daný úhel na tři stejné části (této úloze se říká trisekce úhlu) nebo sestrojit úsečku, jejíž délka by se rovnala délce dané kružnice (v pozměněné podobě se tomu říká kvadratura kruhu). Mnozí se pokoušeli takové úlohy řešit a někteří se o to pokoušejí stále, i když v 19. století bylo dokázáno, že tyto úlohy vyřešit pomocí pravítka a kružítka nelze. Důkazy, že něco nejde, bývají zpravidla složitější než důkazy, že něco jde, a lidé mívají někdy sklon takové argumenty přehlížet. Týká se to jak matematiky a informatiky, tak argumentů, které předkládá logika v teorii či filozofii vědy.

Občas mají zdánlivě pravdu, protože někdy stačí připustit jiné prostředky či postupy a problém se vyřeší. Ostatně trisekci úhlu nebo rektifikaci (napřímení) kružnice přece s dostatečnou přesností umí udělat každý a přibližných konstrukcí lidé vymysleli spousty. Nebo lze postupovat tak, že se rozšíří přípustné prostředky. Právě toho se týkal příběh Jak přijít úsečce na kloub (Vesmír 87, 258, 2008/4). Dovolilo se používat složitější nástroje – kloubové mechanismy, otázka se ale zase vrátila. Co se takovými mechanismy udělat dá a co ne? Ocitli jsme se v oblasti ne už elementární geometrie, nýbrž geometrie algebraické. Otázka tehdy zněla, zda se dá pohyb po přímce převést kloubovým mechanismem přesně na pohyb po kružnici. To se znamenitým matematikům a fyzikům tak dlouho nedařilo, až někteří dospěli k přesvědčení, že přesně to vůbec udělat nelze, podobně jako nelze pravítkem a kružítkem přesně provést trisekci úhlu. K překvapení všech se pak ukázalo, že to jde, a navíc velmi jednoduše.

Kloubovými mechanismy lze přesně provést trisekci úhlu, nelze však přesně vyřešit kvadraturu kruhu. Dvakrát bylo v předchozí větě slovo „přesně“: rozumí se ideálním pravítkem, ideálním kružítkem, ideálním kloubovým mechanismem a v dalším vyprávění to bude ideálním skládáním (přehýbáním) papíru.

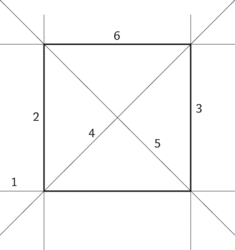
Náš příběh začíná otázkou: Co se dá udělat skládáním papíru? Přehnete-li papír, dostanete přímku (naposledy: ideální papír = rovina, přehnutý papír = ideální přímka), přeložíte-li ještě jednou, dostanete jinou přímku, a pokud se obě protnou, dostanete bod. Čtverec se zkonstruuje snadno:

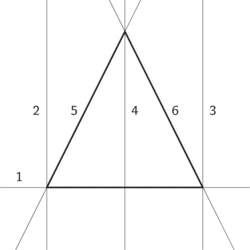
Ještě jedna snadná úloha: sestrojit rovnoramenný trojúhelník. Několik takových trojúhelníků už máte na předcházejícím obrázku. K následujícímu obrázku poznamenejme jen tolik, že přímka 4 je rovnoběžka půlící vzdálenost mezi 2 a 3, a získá se přehnutím papíru tak, aby 2 přešla na 3. Ostatní se už jistě obejde bez slovního popisu.

To byl trojúhelník rovnoramenný. A co trojúhelník rovnostranný? A pravidelný pětiúhelník? A dále: Sestrojili jsme nějaký čtverec a nějaký rovnoramenný trojúhelník. Lze sestrojit (a jak?) přehýbáním papíru čtverec s (někde) zadanou stranou? A podobně to lze říci pro ostatní konstrukce. Jinak řečeno máme dánu úsečku dvěma body (tedy a naposledy dvěma body, které vznikly jako průsečíky přehybů papíru). Dokážeme tuto úsečku přesunout na dané místo a do daného směru? Pokud si myslíte, že by to neměl být problém, zkuste si to udělat. Je zvláštní, že se tyto otázky začaly klást ve srovnání se stářím geometrie až hodně pozdě. A ještě podivnější je, odkud takové otázky přišly.

V roce 1893 vyšla v Madrásu kniha indického výběrčího daní (na titulním listě uvádí, že je „deputy collector“) T. Sundary Rowa¹⁾ Geometrical Exercises in Paper Folding. V úvodu píše, že na počátku byl dárek pro mateřské školky „Kindergarten Gift No. VIII. – Paper Folding“, skládající se z krabičky se 200 čtvercovými papíry, po jedné straně barevnými a lesklými, a s návodem. Patrně šlo o to, čemu nyní říkáme origami (proto se také někdy té geometrii, jíž se zpočátku budeme zabývat, říká „origamová geometrie“). I Rowovu knihu doprovázela krabička se stovkou papírků (tady se projevilo omezení internetu). V knize jsou pak desítky geometrických konstrukcí, které lze uskutečnit přehýbáním papíru.

Pozoruhodné je, že Rowova (či Raova) práce neunikla pozornosti tehdejší vůdčí postavy geometrie Felixe Kleina, který se o ní zmiňuje ve svých přednáškách o vybraných otázkách elementární geometrie.²⁾ Projevili o ni zájem i další matematici, zvláště W. W. Beman a D. E. Smith, kteří připravili revidovaná vydání; poslední – pokud je mi známo – vyšlo v roce 1966. Zájem o takovou papírovou geometrii se objevil znovu až v polovině devadesátých let, kdy byly zveřejněny některé nečekané konstrukce. Jedna z nich je tak překvapivá, krásná a jednoduchá, že se na ni společně podíváme. Přivede nás také k nutnosti ujasnit a upřesnit si prostředky (či operace), které používáme při skládání papíru.

Vyjdeme z obdélníku (ten už umíme poskládat); můžeme ovšem použít už hotový obdélník – list papíru. Přehneme tak, jak je na obrázku (volba směru přehybu je na vás):

Nyní papír přehneme dvakrát tak, aby vzdálenost mezi rovnoběžkami byla stejná. Nejjednodušší je papír přehnout v polovině a pak ještě jednou v dolní polovině (horní přímka nemusí však nutně být v polovině obdélníku):

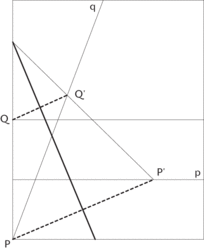
Nyní přijde nejsložitější operace. Musíme najít přímku („tučnou“) takovou, že když podle ní přehneme papír, přejde bod P do bodu P′ na přímce p a bod Q do bodu Q′ na přímce q:

Přímka přehybu se vyhledá jemným nastavováním okraje papíru, až dostaneme bod P na přímku p a současně bod Q na přímku q. Nyní zbývá ještě rozpůlit úsečku P′Q′ (nebo úhel P′PQ′). To můžeme udělat přeložením papíru tak, aby PP′ přešla na PQ′:

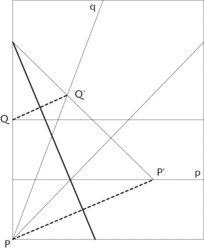
Výsledek (po doplnění ještě chybějících přehybů) vypadá takto:

Jestliže si obrázek prohlédnete podrobně (návodem je značení úseček a úhlů), zjistíte, že jste provedli trisekci úhlu α = 3β.

Je to konstrukce tak jednoduchá, že si vůbec nedovedu představit, jak se na ni může přijít. Připisována je Japonci Hishasi Abemu, který s ní přišel někdy v sedmdesátých letech. Zveřejnil ji v roce 1980 K. Husimi, jenže japonsky, a tak se o ní ta část světa, která japonsky nemluví, dověděla až v roce 1996.³⁾

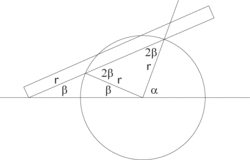
Je to elegantní a snad i zábavný výsledek, jehož půvab vyvstane ještě zřetelněji ve srovnání s tradičním způsobem trisekce úhlu pomocí proužku papíru:

Rozdělit se má úhel α. Nakreslí se kružnice se středem ve vrcholu úhlu a s libovolným poloměrem r, který se nanese na proužek papíru, s nímž se pak manipuluje tak dlouho, až se jeden konec ocitne na vodorovné přímce, druhý na kružnici, a proužek prochází průsečíkem horního ramene úhlu s kružnicí. Tato konstrukce vyžaduje rovněž jemnou a šikovnou manipulaci s proužkem papíru, navíc zde body umisťujeme nikoli na dvě přímky, nýbrž na přímku a kružnici.

Je jistě jasné, že Abeho trisekce úhlu patří do té části matematiky, která je sice půvabná a zábavná, ale rozhodně je to oblast mimo zájem „velké“ matematiky. Podobně je tomu ovšem i s ostatními konstrukcemi vytvářenými skládáním papíru.

Pokud by můj příběh měl skončit u takových kuriozit, nevyprávěl bych jej. Na matematice (a vědě vůbec) je úžasné to, že se věci zcela jednoduché mohou najednou přeměnit v neobyčejně složité a zavést nás do nečekaných oblastí. To se nám v tomto příběhu stane. Najednou se ocitneme s matematiky začátku 20. století před tehdy nedostupnými vrcholky.

Musíme ale postupovat pozvolna. Napřed si vyjasníme, co jsme to vlastně při naší trisekci provedli, jak je možné, že jsme toho skládáním papíru dosáhli více, než se dá uskutečnit pravítkem a kružítkem. Toto druhé dějství našeho příběhu (v příštím čísle Vesmíru) se bude rovněž pohybovat na zcela elementární úrovni, nicméně bude vyžadovat jistou vynalézavost.