Jak přijít úsečce na kloub

Jako každý příběh, dá se i tento říci několika slovy. Jenže pak už to není příběh, ale jeho obsah – jako když někomu vyprávíme obsah filmu či románu. Nebo když se podíváme předčasně na konec detektivky, abychom se dověděli, kdo je vrah. Právě v tom možná spočívá problém vyučování, totiž že se místo příběhů sdělují jejich obsahy, a navíc se všechno prozradí předem.

Vyprávění příběhů matematických je dost riskantní záležitost; říkává se, že každá formulka zredukuje počet čtenářů na polovinu. Zkusil jsem proto vyprávět tento příběh paralelně ve slovech (a formulkách) i v obrázcích (takový matematický komiks).

Papír, tužka a koš na odpadky

Hned na začátku by ale bylo dobré, abyste si ověřili, zda vůbec chcete ve čtení (či prohlížení) pokračovat a zda mne chcete následovat do onoho zapadlého kouta geometrie. Zjistit, zda jste dostatečně geometričtí, abyste mohli vstoupit (jak varoval údajný nápis nad vchodem do Akademie). Je dobré (vlastně nutné) se na cestu vybavit tužkou, papírem (a košem na odpadky, jak říká stará známá anekdota).

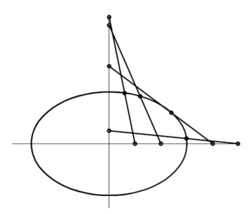
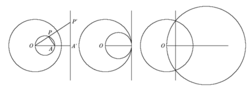
Nuže, máme dvě na sebe kolmé osy a úsečku AB, která jedním koncem klouže po jedné ose a druhým po druhé (obrázek 1). Křižovatka os je průchozí oběma směry (takže bod A „projede“ křižovatkou dolů a začne za sebou stahovat bod B, který po čase projede křižovatkou vodorovným směrem atd.). Na naší úsečce je bod P a otázka zní, jak bude vypadat jeho dráha (jakou opíše křivku), oběhne-li úsečka AB dokola kolem průsečíku os. To není řečnická otázka – máte se pokusit odpovědět dříve, než budete popřípadě pokračovat ve čtení.

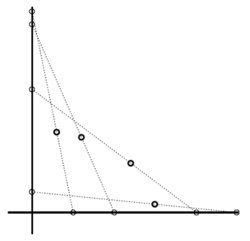
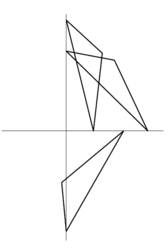Můžeme začít experimentovat: nakreslit osy a místo úsečky použít proužek papíru, který budeme k osám přikládat. Na obrázek 2 je několik možných poloh úsečky a několik poloh bodu P. Vypadá to (možná proti původní intuici, tj. názoru) na něco vypouklého a oválného.

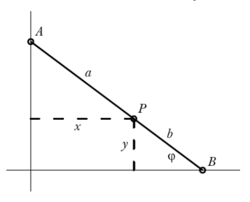
Pokusíme se vypočítat souřadnice x a y bodu P v závislosti na úhlu φ (obrázek 3).

K tomu budeme potřebovat základní vztahy trigonometrie

x/a = cos φ, y/b = sin φ, tedy x²/a² + y²/b² = cos²φ + sin²φ = 1

a ovšem ještě potřebujete vědět, že to, co jsme dostali, je rovnice elipsy. Ta je na obrázek 4.

Pokud by bod P byl uprostřed úsečky AB, tedy a = b, opisoval by bod P kružnici s poloměrem a. Na kreslení kružnic máme sice kružítko, naše zařízení však dovoluje kreslit elipsy (a skutečně bylo základem přístrojů zvaných elipsografy).

Tímto příkladem jsme se dostali do té části geometrického světa, kde se zkoumají možnosti mechanického kreslení křivek. Můžete si vše vyzkoušet na mírně složitější úloze, v níž místo úsečky bude klouzat trojúhelník (obrázek 5). Lze to opět vyzkoušet experimentálně, trojúhelník bývá ještě někdy po ruce. Pokud to opravdu zkusíte, možná budete překvapeni. Školní trojúhelníky jsou totiž pravoúhlé – a co dostaneme, když je pravý úhel právě u toho vrcholu, který opisuje křivku? Stojí za to vyzkoušet to.

Hra s trojúhelníky

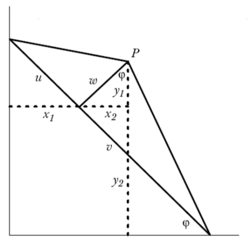
Teď trochu počítání. Výšku trojúhelníku si označme w. Základnu trojúhelníku výška rozdělí na dvě části u a v (viz obrázek 6). Chceme vypočítat souřadnice bodu P v závislosti na jednom parametru – úhlu φ, který svírá základna trojúhelníku s osou x. Vedeme tečkované úsečky, jak je to na obrázku, a jejich části si označíme x₁, …

Opět budeme potřebovat jen základní vztahy trigonometrie:

x₁/u = cos φ, x₂/w = sin φ,

y₁/w = cos φ, y₂/v = sin φ,

z nichž dostaneme hledané parametrické vyjádření křivky opisované bodem P:

x = x₁ + x₂ = u · cos φ + w · sin φ,

y = y₁ + y₂ = w · cos φ + v · sin φ.

Jednoduchými úpravami dostaneme následující vztahy:

wx – uy = (w² – uv) sin φ,

vx – wy = (uv – w²) cos φ.

Umocníme na druhou a sečteme

(wx – uy)² + (vx – wy)² = (uv – w²)²,

což je (neparametrická) rovnice naší křivky – vztah souřadnic x a y těch bodů, které leží na křivce. Je to křivka druhého stupně (nejvyšší mocnina v rovnici je 2; druhého stupně je i hyperbola xy = 1), a tedy kuželosečka; dokázat, že je to elipsa, je už věcí rutinní. (Trochu zběhlejší v matematice uvidí v posledním vztahu rovnici kružnice a i odpovídající změnu souřadnic – lineární transformaci – která z kružnice udělá elipsu.) Zajímavý je případ, kdy uv – w² = 0: elipsa „degeneruje“ na úsečku. Pokud jste skutečně chvilku experimentovali a použili jste pravoúhlý trojúhelník, pak jste možná zpočátku formulovali chybnou hypotézu – totiž že se vrchol pohybuje vždy po úsečce. Vztah uv – w² = 0 charakterizuje přesně pravoúhlé trojúhelníky (uměli byste to dokázat?).

Hlouběji do zákoutí

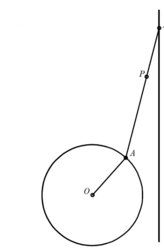
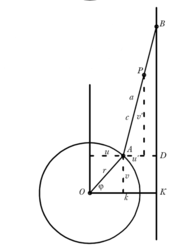
Postoupíme hlouběji do našeho zákoutí: úsečka bude teď jedním koncem klouzat po přímce, druhým po kružnici (obrázek 8). Opět můžeme snadno experimentovat a pokusit se odhadnout výslednou křivku. Vše je zde ale složitější, a proto se pokusíme získat rovnici křivky opisované bodem P. Poloměr kružnice označíme r, vzdálenost přímky od středu kružnice k (|OK| = k), klouzající úsečka AB má délku a (|AB| = a) a vzdálenost bodu P, jehož dráha nás zajímá, od bodu A je c (|AP| = c) (obrázek 9).

.

Zavedeme-li si funkci

p(φ) = (k – r · cos φ)/a,

dostaneme

a nakonec i parametrické vyjádření souřadnice bodu P

.

Jak to dopadne v případě r = 3, k = 4, a = 8, c = 5, ukazuje obrázek 10.

Ještě si (naposledy) započítejte, poku síme se získat rovnici naší křivky.

Z našich vztahů odvodíme p(φ) = (k – x)/(a – c) = (k – x)/(b) (b = a – c). Dosadíme do posledního vztahu a počítáme, počítáme a počítáme – až dostaneme rovnici:

[b(x² + y² + c² – r²) + 2cx(x – k)]² + 4c²y²(k – x)² = 4b²c²y².

Je to tedy algebraická křivka čtvrtého stupně. Algebraické jsou ty křivky, jejichž rovnice je mnohočlen dvou proměnných x a y; stupeň křivky je pak nejvyšší mocnina (tím se myslí i součiny – x³ · y² je 5. stupně). Nealgebraickým křivkám se říká transcendentní; příkladem může být y = sin x. K tomuto rozdělení křivek se vrátíme v závěru našeho příběhu.

Geniálně prosté

Algebraické křivky vyšších řádů mají složitější (a zajímavější) průběhy. Tak naše křivka může nabývat různých podob podle volby parametrů. Několik příkladů najdete na obrázek 11, obrázek 12, obrázek 13. Když pak další případ (3 0 9 7) nakreslíme trochu jinak (obrázek 14), ocitneme se v říši technických křivek: úsečka AB je teď ojnice, bod B opisuje kružnici, bod A jezdí po úsečce a bod P opisuje naši křivku. 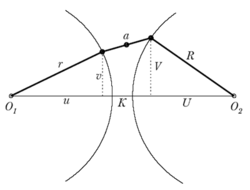V říši technických křivek ještě chvíli zůstaneme. Vrátíme se do roku 1784, kdy James Watt narazil na problém jak v parostroji převést pohyb pístu na pohyb kruhový tak, aby píst ve válci co nejméně „drhnul“. Jeho řešení bylo geniálně prosté (a Watt si ho cenil více než svého slavného regulátoru, který se později stal ikonou kybernetiky). Úsečku necháme klouzat po dvou kružnicích (obrázek 15); bude tedy mezi nimi „kvedlat“, čímž se vyrovnají odchylky a střed úsečky se bude pohybovat přibližně po přímce. Opět zde můžeme experimentovat a kružítkem si nakreslit množství bodů křivky. Mohli bychom začít i počítat: K je vzdálenost středů obou kružnic, r, R jejich poloměry (na obrázku i ve Wattově případě byly poloměry stejné, a je délka klouzající úsečky. Máme pak

u² + v² = r², U² + V² = R²,

(K – u – U)² + (V – v)² = a²

a z toho (a z podobných vztahů pro jiné typy poloh úsečky) se můžeme pokoušet získat rovnici křivky. Napřed bychom třeba dostali nějaké parametrické vyjádření (parametrem může být například u; musel jsem to udělat, abych mohl na počítači nakreslit výslednou křivku). Výsledná rovnice Wattovy křivky v proměnných x a y je velice komplikovaná, nepřehledná a do hezkého tvaru se dá dostat jen velmi rafinovanou volbou souřadnicového systému. Jedno se ale při těchto výpočtech zjistí snadno: Je to algebraická křivka šestého stupně. Jedna její podoba je na obrázek 16. Důležitá je střední část – tam se střed klouzající úsečky pohybuje téměř po úsečce, tedy tak, jak to Watt potřeboval. Wattova křivka může ovšem nabýt pro jiné parametry překvapivých podob: na obrázek 17 je případ, kdy a > K. Když obrázek otočíte, uvidíte úsečku zavěšenou na dvou čepech – přidejte tam lavičky, popřípadě stolek doprostřed a dostanete takovou tu zahradní rodinnou houpačku. Řeknete: taková hloupá houpačka a ona si opisuje algebraickou křivku šestého stupně.

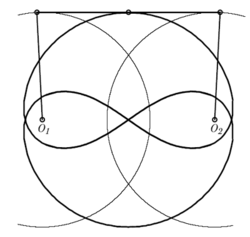
Vývoj dokonalejších maziv odsunul původní teoretický problém do pozadí. V následujících desetiletích se ma tematici pokoušeli převést kloubovými mechanizmy pohyb po kružnici na pohyb po úsečce (a obráceně). Marně. A nemuselo by jít o pohyb po celé kružnici, stačil by pohyb po jejím oblouku, po sebemenším kousku (to je ukázáno na obrázek 18).

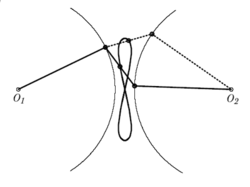
Z kružnice úsečka a naopak V polovině devatenáctého století se po mnoha marných pokusech dospělo k přesvědčení, že takový přesný převod vůbec není možný. Ostatně tomu napovídala i intuice: jak byste chtěli z kruhových otáčivých pohybů složit přesně pohyb přímý? O nemožnosti tohoto převo du byl zřejmě přesvědčen i ruský matematik Pafnutij Lvovič Čebyšev, který vytvořil r. 1858 teorii polynomů nejméně se odchylujících od nuly (přímky). Tyto polynomy dostaly později jeho jméno a staly se velmi důležitými v přibližných numerických řešeních matematických úloh. Na základě této teorie pak Čebyšev konstruoval různé mechanizmy, které převáděly kruhový pohyb na pohyb přímý s daleko vyšší přesností než zařízení Wattovo. Jeden takový kloubový mechanizmus je na obrázek 19. Všimněte si, že je to varianta Wattova čtyřúhelníku: kružnice mají jiné poloměry, jeden poloměr je roven délce klouzající úsečky, nesledujeme pohyb středu úsečky, ale pohyb konce jejího zdvojnásobení (bod P). Počítá se to podobně jako Wattova křivka a dost jsem se s tím nadřel. Výsledek je ale krásný: na obrázek 20 nerozpoznáte dolní část křivky od úsečky.

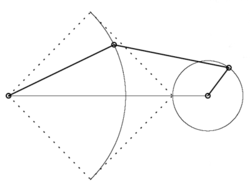
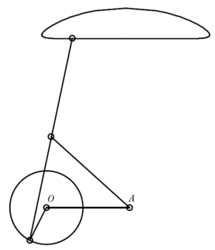
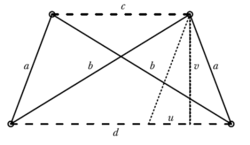
Teď jsem snad dovršil první část příběhu, tu, v níž se některé jednoduché věci ukázaly být neobyčejně složité (převedení přímého pohybu na kruhový nebo pohyb houpačky). Je na čase nastoupit cestu obrácenou: od složitého k překvapivě jednoduchému. Na scénu vstupuje ruský student Lipman Izrailevič Lipman, syn rabína z Koněnské gubernie, jehož vzdělání se skládalo jen ze studia Bible a Talmudu. Samouk, naučil se německy a francouzsky a začal se zabývat matematikou. Odjel do Německa, nejprve do Královce, pak do Berlína a Jeny. Vrátil se do Petrohradu, studia však nedokončil, protože předčasně zemřel. V roce 1868 předvedl – zřejmě k naprostému údivu Čebyševa – jednoduché řešení problému převodu přímého pohybu na kruhový velmi prostým kloubovým mechanizmem. ¹⁾ Rusko se ovšem tímto objevem pochlubilo na mezinárodní výstavě ve Vídni v roce 1873. To probudilo Francii: totéž zařízení vynalezl totiž už v roce 1864 jejich důstojník, absolvent Polytechniky (a pozdější generál) CharlesNicolas Peaucellier. Jeho vynález byl i zveřejněn, ale nějak unikl pozornosti. Francie pak Peaucellierovi udělila hned významnou cenu Prix Montyon. Paucellierův kloubový mechanizmus („inverzor“) najdete na obrázek 21.

Dvě úsečky mají délku a a zbývající čtyři délku b, přičemž a > b. Krátký a jednoduchý výpočet (v němž dvakrát použijeme Pythagorovu větu) dá:

|OP| = u, |OP'| = u + 2v,

a² = (u + v)² + c² = u² + 2uv + v² + c²

= u² + 2uv + b²,

|OP| · |OP'| = u · (u + 2v) = u² + 2uv = a² – b².

Inverze a inverzory

Teď ale musím udělat odbočku a povědět něco o inverzi. To je zvláštní transformace roviny, která obrací vnitřek daného kruhu „naruby“ (a vnějšek tohoto kruhu na jeho vnitřek). Inverze je dost pozdním vynálezem (r. 1831, L. Magnus). Tato transformace je definována takto: inverze vůči kružnici se středem O a poloměrem r přiřazuje bodu P bod P' na přímce spojující střed O s bodem P tak, že je splněna podmínka |OP| · |OP'| = r². Na obrázek 22 je ukázána i jednoduchá konstrukce bodu P'; trojúhelník je pravoúhlý. Výška dělí velký trojúhelník na dva menší, které jsou si podobné, takže OP : r = r : OP'. Inverze ponechává body kružnice na místě. Z obrázku je také vidět, že se skutečně body vnitřku kruhu zobrazují na jeho vnějšek (čím blíž jsou středu, tím dál je jejich obraz) a obráceně. Matematici si vyprávějí matematické vtipy (kterým se smějí jen oni sami). Povím vám klasický vtip o inverzi. ²⁾ Víte, jak matematik chytí lva? Jednoduše. Zavře se do kruhové (kulové) klece a lva nechá před klecí. Pak provede inverzi – a lev je v kleci, matematik venku.

Peaucellierův inverzor realizuje inverzi vzhledem ke kružnici se středem O a poloměrem a² – b² (dokázali jsme přece právě, že |OP| · |OP'| = a² – b²).

Inverze má některé pozoruhodné jednoduché vlastnosti. Pro nás nejdůležitější je, že přímky neprocházející bodem O převádí na kružnice procházející bodem O (s vyjmutím bodu O samého – ten by odpovídal nekonečnu). Na obrázek 23 jsou nakresleny tři možné případy: přímka je vně kružnice, přímka se kružnice dotýká a přímka kružnici protíná. Důkaz provedeme jen pro první případ. Je velmi jednoduchý (stále doufám, že si zkusíte důkaz najít dříve, než budete pokračovat ve čtení – jinak přijdete o moc). Trojúhelníky OPA a OA'P' jsou pravoúhlé a jsou si podobné. Proto

|OP| : |OA| = |OA'| : |OP'|,

a tedy

|OP| · |OP'| = |OA| · |OA'| = r²,

a podobně ve zbývajících dvou případech.

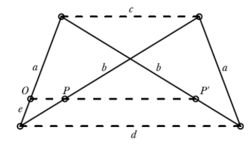
Peaucellierovo zařízení dostaneme, přidáme-li ještě jednu úsečku SP tak, aby kružnice se středem S a poloměrem |SP| procházela bodem O (viz obrázek 24). Body S a O fixujeme. Pohybujeme-li bodem P tak, aby opisoval oblouk kružnice do bodu Q, bude bod P' opisovat úsečku do bodu Q' (bod Q' je obrazem bodu Q). Z vlastností inverze plyne, že úsečka P'Q' je rovnoběžná tečně ke kružnici v bodě O.

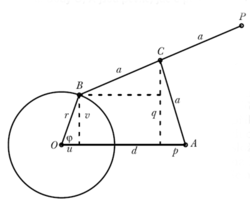
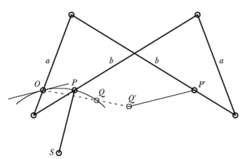
Peaucellierův mechanizmus byl předveden v Anglii v lednu roku 1874 matematikem Sylvestrem na přednášce v Royal Institution. Sylvester byl tímto vynálezem tak nadšen, že jej pokládal za počátek nové éry v matematice, a o něco později dokonce přišel s nápadem, že by celý vesmír mohl být jeden velký kloubový mechanizmus – „cosmic linkage“. V srpnu téhož roku H. Hart z Woolwich Academy předvedl nový kloubový mechanizmus, který se skládal už jen ze čtyř úseček (místo šesti Peaucellierových). Hartův „antiparalelogram“ je na obrázek 25. Úsečky c a d jsou diagonály (úhlopříčky) antiparalelogramu a součin jejich délek zůstává zachován při manipulaci s antiparalelogramem. Při důkazu opět vystačíme s Pythagorovou větou. Doplníme (tečkované) úsečky – jednu rovnoběžnou se stranou a, druhou kolmou na d.

d = c + 2u, cd = c² + 2cu = (c + u)² – u²

(c + u)² + v² = b², u² + v² = a²

cd = b² – v² – u² = b² – a²

Nyní vedeme rovnoběžku s diagonálami antiparalelogramu a její průsečíky se stranami antiparalelogramu označíme O, P, P' – jak je to na obrázek 26. Z podobnosti trojúhelníků (snadno z níže uvedených poměrů zjistíte, o které jde) dostaneme:

|OP|/e = c/a, |OP'|/(a – e) = d/a,

a tedy

|OP| · |OP'| = cd · [e(a – e)]/a²,

kde cd je konstanta, a, e jsou také konstanty, takže toto zařízení opět reali zuje inverzi: bod P' je obrazem bodu P při inverzi se středem O a poloměrem . obrázek 27 ukazuje Hartův inverzor: body O a S jsou pevné, bod P se pohybuje po oblouku kružnice (procházející bodem O!), bod P' po úsečce: bod Q' je obrazem bodu Q. Pohybujeme-li bodem P po oblouku kružnice do bodu Q, pohybuje se bod P' po úsečce až do bodu Q'. Všimněte si, že – jak se sluší a patří – tato úsečka je rovnoběžná s tečnou k oblouku kružnice v bodě O. Dovedete si představit ještě něco jednoduššího? Tak skončila druhá část našeho příběhu – od složitosti k jednoduchosti. A musí přijít coda, vyvrcholení celého příběhu. Příběhu, který vlastně začal už roku 1637.

Kloubový mechanizmus pro libovolnou křivku

V tom roce vyšla v Leydenu Descartova Rozprava o metodě, která obsahovala tři eseje. První z nich, Geometrie, představoval revoluci v matematice,

V druhé knize tohoto eseje Descartes kritizuje rozdělení křivek v řecké matematice na křivky geometrické a křivky mechanické. Geometrické křivky byly ty, které se dají sestrojit pomocí pravítka a kružítka, ostatní křivky vyžadovaly nějaké mechanické zařízení. Byla to zařízení například na rozdělení úhlu na tři stejné části. Descartes namítá: a kružítko snad není mechanický nástroj? Předkládá jiné dělení křivek: na ty, které lze opisovat pomocí tak skloubeného systému úseček, že pohyb jedné z nich vynutí jednoznačně pohyb všech ostatních. Konec jedné z těchto úseček pak opisuje křivku, kterou Descartes nazývá geometrickou. Uvádí příklady a počítá rovnice takových křivek. Všechny křivky, které takto vzniknou, jsou v dnešní terminologii algebraické. Descartes – zdá se – zcela samozřejmě předpokládá, že to platí i obráceně: pro každou algebraickou křivku lze sestrojit takový systém pospojovaných úseček, který opisuje (při vynuceném pohybu jedné z nich) právě tuto křivku (či její – libovolně určenou – část).

Na důkaz existence takového kloubového mechanizmu pro libovolnou algebraickou křivku se muselo dlouho čekat. Vždyť se neuměla nakreslit ani úsečka. V roce 1876, po objevu inverzorů, důkaz správnosti Descartovy domněnky podal anglický matematik A. B. Kempe. Ideu důkazu zde mohu jen naznačit. Kempe sestrojil několik málo kloubových mechanizmů a způsobů jejich kombinování. Pak ukázal, že pro každou algebraickou křivku lze udat mechanický postup (řekli bychom algoritmus), jak z těchto elementárních mechanizmů zkombinovat ten, který křivku reprodukuje. Výsledek je velmi složitý, prakticky nepoužitelný, ale zde šlo o principiální možnost. Ukážu jen jeden z Kempeho kloubových mechanizmů, jemuž říkal reverzor (obrázek 28). Snad v něm na závěr uvidíte půvab všech těchto polozapomenutých mechanizmů.

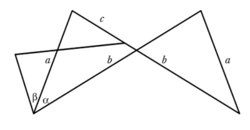
Jak nakreslit úsečku

K Hartovu inverzoru z úseček a a b připojíme menší inverzor složený z úseček c a a, jak je to ukázáno na obrázek 28. Úsečka c se volí tak, aby splňovala následující poměry b : a = a : c. To totiž zajistí, že oba inverzory – větší i menší – jsou podobné. Důsledkem toho je, že když nastavíme na velkém inverzoru nějaký úhel α, bude odpovídající úhel v menším inverzoru β = α.

Kempe říkal tomuto složenému kloubovému mechanizmu reverzor. Lze se totiž na něj dívat tak, že úhel α obrací symetricky na druhou stranu. Teď si představte, že vše zopakujete, připojíte další, ještě menší inverzor. Při nastaveném úhlu a se na druhé straně objeví tento úhel dvakrát. Když přidáte další inverzor, bude tam trojnásobek původního úhlu. Máte multiplikátor: zopakujeteli n-krát, dostane pro daný úhel jeho n-násobek.

Kloubové mechanizmy rozmanitých typů byly v devatenáctém století natolik oblíbené, že se staly součástí sbírek vědeckých přístrojů. Obrázky mnoha takových mechanizmů obsahuje Kempeho kni ha z roku 1877, která vznikla z populární Kempeho přednášky a která měla krásný provokující název: Jak nakreslit úsečku.