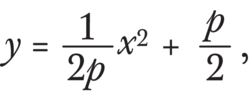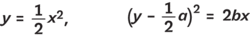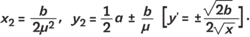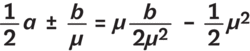Origamová geometrie

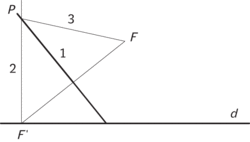
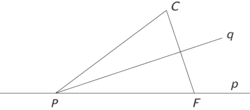
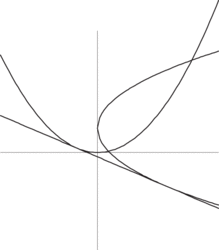
Pokud jste si tehdy postup vyzkoušeli, vzpomenete si snad, že se tam musel najít takový přehyb papíru, aby se při něm dva dané body ocitly na dvou daných přímkách. Zkusme si to vyjasnit pro jeden bod a jednu přímku: Daná přímka je d a bod mimo ni F. Přehneme papír (jakkoli) tak, aby se bod F ocitl na přímce d. To lze udělat ovšem nekonečně mnoha způsoby, bod F se může ocitnout v kterémkoli bodě přímky d.

Na obrázku jsme papír přehnuli podle přímky 1, přičemž bod F přešel do bodu F‘. V bodě F‘ jsme vztyčili kolmici, která proťala přímku 1 v bodě P. Vzdálenost P od bodů F a F‘ je tedy stejná. Otázka nyní zní: budeme- li měnit přehyby papíru, tj. bodu F‘, jak bude vypadat geometrické místo odpovídajících bodů P? Jakou křivku tyto body opíší?

Zde je chvilka na experimentování: najít více takových bodů P a pokusit se uhádnout, na jaké křivce leží. Pokud se vám to podaří (a výsledek jste předem neznali), možná vás to překvapí: je to parabola. Není obtížné to dokázat, stačí k tomu elementární matematika (měla by vám vyjít rovnice

v níž p je vzdálenost ohniska F od řídicí přímky d). A umíte-li počítat ještě trochu víc, zjistíte snadno, že přehyb papíru (přímka 1 na obrázku) je tečna k této parabole.

Teď už známe odpověď na naši poslední otázku: při trisekci úhlu jsme hledali takový přehyb (přímku), aby současně přešly dva body na dvě přímky, tedy hledali jsme společnou
tečnu ke dvěma parabolám. Umíme-li nalézt takovou společnou tečnu, pak umíme vyřešit rovnice třetího stupně, tudíž i uskutečnit trisekci úhlu. Dokázat to je sice snadné, ale přece jen to chce trochu obratnosti.

Postup je ukázán v textu v rámečku. Pokud jste si trisekci úhlu přehýbáním papíru zkoušeli, pamatujete si také, že nalezení přehybu – společné tečny – vyžadovalo jistou zručnost. Něco takového nemůžeme pokládat za jednoduché skládání papíru. Zkusme být skromnější a dovolme jen tyto jednoduché operace, které už formulujeme v jazyce geometrie:

1. Spojit dva body přímkou.

2. K dané přímce vést někde kolmici.

3. Rozpůlit daný úhel.

Tyto jednoduché operace stačily na všechny dosud zmíněné úlohy (kromě trisekce úhlu), dokonce jsme pomocí nich dokázali nacházet body paraboly a tečny v těchto bodech. Zkuste si vyřešit s použitím těchto operací jednoduchou úlohu: dány jsou dvě rovnoběžky, máme najít rovnoběžku uprostřed mezi nimi.

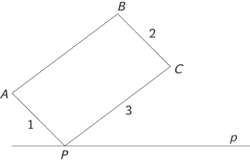
Následující úloha vypadá také jednoduše: Dána je přímka p a bod P mimo ni. Máme vést rovnoběžku k p bodem P. Stojí za to zkusit si to udělat dříve, než si přečtete výklad v popisce obrázku 2.

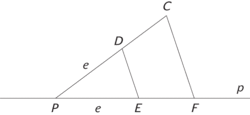
Další důležitou úlohou je přenos dané úsečky na dané místo a do daného směru. Máme tedy přenést danou úsečku na přímku p od bodu P. První krok: Úsečku přeneseme tak, aby začínala v bodě P. K tomu stačí, jestliže umíme vést rovnoběžky daným bodem:

Druhý krok spočívá ve „sklopení“ úsečky PC na přímku P. Napřed vedeme přímku q, půlící úhel, který svírá přímka PC s přímkou p, a pak spustíme na přímku q kolmici z bodu C, průsečík této kolmice s p je F: AB = PC = PF.

Shrňme dosavadní výsledky. Skládáním papíru dokážeme vést přímky danými body, půlit úhly, vést kolmici daným bodem a přenášet úsečky.

Tady bude v našem příběhu bod obratu. Ocitneme se v jiné oblasti geometrie. Zkusme tedy vše začít v opačném pořadí: Připustíme jen vedení přímky danými dvěma body (tj. „pravítko“) a přenos úsečky na dané místo a v daném směru. Dokážeme pak uskutečnit všechny ty konstrukce, které umíme udělat skládáním papíru? Projděme všechny čtyři operace:

1. Vést rovnoběžku daným bodem: na přímce zvolíme libovolnou úsečku e a přeneseme ji vedle. Ostatní jako výše.

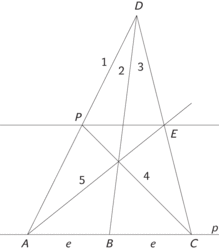
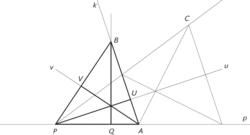
2. Vést někde kolmici k dané přímce p. Kupodivu je to dosti komplikovaná úloha. Na přímce p zvolíme libovolně bod P a vedeme jím libovolně přímku PC (C neleží na p). Předcházející konstrukcí rozpůlíme úhel, který svírá tato přímka s P: dostaneme přímku u a kolmici k na ni. Tato kolmice protne p v bodě A. Bodem A vedeme opět libovolnou přímku a stejnou konstrukcí rozpůlíme odpovídající úhel a dostaneme osu v a kolmici na ni; tato kolmice protne k v bodě B. Tak dostaneme trojúhelník PAB a dvě jeho výšky. Třetí výška (spojnice vrcholu B a průsečíku obou výšek) je třetí výška, která je kolmá na přímku p.

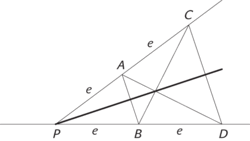
3. Rozpůlit úhel. Průsečík přímek je P. Na obě přímky naneseme dvakrát za sebou úsečku e. Spojíme AB a CD přímkami: přímka mísspojující bod P s průsečíkem těchto přímek je hledaná osa úhlu.

A máme tady výsledek: Jednoduchým skládáním papíru lze udělat přesně totéž jako pravítkem a přenášením úsečky. Stačí dokonce umět přenášet jen jednu danou úsečku, etalon (to byla úsečka e). Upozornil na to maďarský matematik Josef Kürschák v r. 1902. K tomu je třeba ovšem ještě doplnit důkaz, že pomocí pravítka a etalonu lze přenést jakoukoli úsečku; stačí jen ukázat, že lze jakoukoli úsečku sklopit. Kürschákovo řešení je v druhém rámečku.

Protože pomocí pravítka a kružítka umíme přenášet úsečky, je jasné, že vše, co můžeme udělat pomocí pravítka a etalonu, můžeme udělat i pomocí pravítka a kružítka. Obráceně to neplatí, nelze třeba sestrojit pravoúhlý trojúhelník, je-li dána odvěsna a jedna přepona. Dokázat to není jednoduché, podařilo se to Davidu Hilbertovi. Ale ani ten nedokázal odpovědět na otázku, co se přesně dá udělat, a tak ji zařadil v roce 1900 mezi své slavné problémy pro 20. století. Vyřešit se jej podařilo Artinovi až v roce 1927. Jeho řešení však nebylo konstruktivní: vědělo se co, ale ne jak. To vyřešili o dalších 30 let později logici Abraham Robinson a Georg Kreisel. Jenže jejich algoritmus je beznadějně časově složitý, tedy neproveditelný ani na nějakých superpočítačích. A vysvětlit to vše stručně a srozumitelně také není jednoduché, a tak nezbývá než odkázat na mé podrobnější zpracování pro 32. mezinárodní konferenci o historii matematiky (Matfyzpress 2011, s. 11–32).