O převaze vzácnosti v přírodě

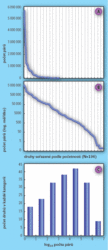
Biology fascinuje na přírodě její rozmanitost. Nemusíme být ale biologem, abychom si všimli, že příroda je na každém místě trochu jiná. Všude najdeme trochu jiné druhy, a čím dále jdeme krajinou, tím větší různorodost zaznamenáme. Když navíc začneme jedince jednotlivých druhů počítat – což je první krok k ekologii, která byla mimo jiné definována jako věda o početnosti a rozšíření organismů – upoutá nás ještě jedna zajímavost. Naprostá většina organismů je vzácných: vyskytují se jen na velmi omezeném území, a navíc vesměs řídce. Jde o zcela univerzální zákonitost, kterou pozorujeme, ať už sledujeme populace v rámci celých kontinentů, nebo třeba jen malinkých plošek (obr. 1 a 4). Když seřadíme druhy od nejpočetnějšího k nejméně početnému, je těch opravdu hojných na začátku našeho žebříčku jen hrstka – potom početnost strmě klesá a následuje dlouhý „ocas“ poměrně vzácných druhů (obr. 2A). Jestliže ale vyjádříme populační početnosti v logaritmickém měřítku, tedy jestliže zlogaritmujeme hodnoty na svislé ose (obr. 2B), budou mnohem vyrovnanější. Když tyto zlogaritmované hodnoty vyneseme do histogramu, bude mít přibližně tvar zvonu upomínajícího na normální (tj. Gaussovo) rozdělení (obr. 2C). Normálnímu rozdělení zlogaritmovaných hodnot se říká logaritmicko- normální nebo lognormální, a dlouho bylo považováno za nejlepší model rozdělení vzácnosti a hojnosti druhů v přírodě (viz Vesmír 76, 495, 1997/9 a 77, 263, 1998/5).

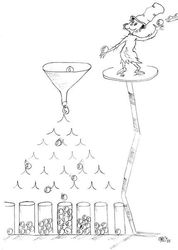
Jaký proces by mohl k takovému rozdělení vést? Jednou možností je nerovnoměrné dělení zdrojů mezi druhy ve společenstvu. Představme si například neobydlený ostrov, na nějž přijde druh, který si uzurpuje libovolnou, dejme tomu náhodně velkou část zdrojů. Další příchozí se musí spokojit se zbytkem (nebo nějakou jeho náhodnou částí), anebo si uzurpovat část zdroje využívaného druhem, který už se na ostrově vyskytuje. Pěkný, dnes již klasický model tohoto procesu představuje hůl, reprezentující všechny zdroje našeho ostrova. Tu zlomíme na náhodném místě, vybereme náhodně jeden ze dvou vzniklých kousků, ten zase na náhodném místě zlomíme, vybereme náhodně jeden ze tří vzniklých kousků, náhodně zlomíme, vybereme, zlomíme, vybereme… a tak dále, dokud nezískáme stejný počet kousků, jako je druhů v modelovaném společenstvu. Vtip je v tom, že kousky určené k zlomení vybíráme nezávisle na jejich velikosti, takže maličké kousky mají stejnou pravděpodobnost, že budou dále rozdrobeny, jako kousky velké. Tak vznikne spousta malých a jen pár velkých kousků. Zkonstruované rozdělení bude mít podobné statistické vlastnosti jako pozorované rozdělení velikostí populací; bude téměř lognormální.

Tento populární model postupného lámání hole bychom mohli pokládat za realistický, pokud bychom předpokládali, že početnosti odrážejí množství zdrojů, které mají druhy k dispozici (museli bychom například zanedbat, že druhy s malými jedinci by nejspíš měly početnější populace, i kdyby měl každý druh k dispozici stejné množství zdrojů). Ve skutečnosti je ale spousta jiných možností, jak pozorované rozdělení vysvětlit. Robert May, enfant terrible teoretické ekologie (viz rámeček Robert May), přišel v sedmdesátých letech minulého století s myšlenkou, že rozdělením populačních početností se nemá vůbec smysl zabývat, poněvadž lognormální rozdělení vznikne jakýmkoli náhodným multiplikativním procesem, tedy takovým, kdy se mezi sebou různé veličiny náhodně násobí (obr. 3). Postupné rozdělování zdrojů je jen jedním z nich – dělíme náhodně vygenerovaná čísla, reprezentovaná délkou jednotlivých kousků hole, což je totéž jako násobit náhodně vybrané číslo náhodně zvoleným číslem mezi nulou a jedničkou. Přestože od té doby vznikla plejáda modelů s různě přesvědčivou biologickou interpretací, většinový názor se přiklonil k Mayovi, jenž lognormalitu považuje za univerzální a triviální rys přírody, který je možné pozorovat vždy a všude.

Je rozdělení populačních početností invariantní vůči změně plochy?

Jenže právě v té univerzalitě je háček. Je vůbec možné pozorovat tentýž jev současně v lokálním měřítku i na mnohem větších plochách? Představme si dvě plochy vedle sebe, přičemž na každé pozorujeme lognormální rozdělení populačních početností. Pokud by mělo být nějaké rozdělení univerzální, měli bychom ho pozorovat i na ploše vzniklé sloučením těchto dvou ploch. Vcelku jednoduchá matematická analýza ukáže, že to možné není – přesně řečeno, je to možné, jen když se budou na obou plochách vyskytovat tytéž druhy, jejichž početnost se bude chaoticky měnit místo od místa, anebo když bude mít každá z ploch své vlastní druhy a rozdělení jejich hojnosti a vzácnosti budou úplně stejná včetně parametrů.¹⁾²⁾ Obojí je v přírodě prakticky vyloučeno. Lognormální rozdělení populačních početností tedy nemůže být univerzální, nemůže platit současně pro různá prostorová měřítka. To ale také znamená, že za pozorovanou převahu vzácnosti nemohou být univerzálně odpovědné multiplikativní procesy typu zmíněného lámání hole. Tím není nutně řečeno, že tyto procesy nemohou hrát roli v některém konkrétním měřítku, třeba v rámci celých kontinentů, kde si v evolučním čase druhy mezi sebou dělí zdroje. Rozdělení pozorovaná na menších plochách by pak vznikla výběrem z tohoto celkového rozdělení, nebyla by lognormální a neexistoval by žádný jednoduchý univerzální vzoreček na to, kolik druhů je hojných a kolik vzácných. Jenže v takovém případě bychom nikdy nevěděli, kde a jak hledat ono „pravé“ lognormální rozdělení, z něhož jsou všechna ostatní odvozena.

Jinými slovy máme tu jednoduché a vcelku výstižné lognormální rozdělení, vznikající jakýmikoli multiplikativními procesy – jenže to univerzálně nefunguje, protože to nemůže platit současně ve více měřítkách. Existuje vůbec statistické rozdělení, které by bylo neměnné navzdory změně měřítka?

Kupodivu ano, a kupodivu vystihuje pozorované rozdělení vzácnosti a hojnosti stejně dobře jako rozdělení lognormální.²⁾ Platí pro něj, že skládáním sousedních ploch získáme rozdělení, jehož matematická podstata (forma příslušného vzorečku) zůstává stejná, jen parametry se plocha od plochy, společenstvo od společenstva liší. Je ovšem poněkud komplikovanější než lognormální (které je, jak jsme si řekli, vlastně normálním rozdělením zlogaritmované veličiny) a na první pohled není jasná jeho biologická interpretace. Proč by se měli ptáci, kytky nebo motýli v různých prostorových měřítkách chovat podle nějakého měřítkově neměnného matematického předpisu?

Převaha vzácnosti jako následek čistě statistických prostorových procesů

Shrňme si to: buď existuje privilegované prostorové měřítko, na kterém se odehrávají podstatné biologické procesy, a jen na něm budeme pozorovat „skutečné“ rozdělení populačních početností, které vůbec má smysl nějak matematicky charakterizovat, anebo existuje rozdělení univerzální, tedy nezávislé na skládání ploch. Empirická data přitom nasvědčují spíše druhé možnosti. To, co vypadá jako hezký vědecký závěr, je ve skutečnosti začátek nového objevu. Můžeme se totiž ptát: není náhodou právě skládání lokálních společenstev do větších celků klíčem k tomu, abychom porozuměli převaze vzácnosti? Co když je to tak, že postupné skládání skoro jakýchkoli rozdělení pro sousedící společenstva povede k pozorovanému rozdělení populačních početností?

Na první pohled to zní divně; víme totiž, že podle centrálního limitního teorému (viz obr. 3) vede skládání různých rozdělení k rozdělení normálnímu, které je mnohem vyrovnanější co do poměru nízkých a vysokých hodnot. Jenže skládání v prostoru je jiné. Zaprvé se některé druhy vyskytují jen na některých plochách, takže nám spojováním neustále přibývají druhy, které se vyskytují jen někde. Tak přibývá vzácných druhů na levé straně rozdělení. Zadruhé populační početnosti sousedních společenstev jsou si podobnější než u vzdálených společenstev, jsou tedy prostorově autokorelované. Když je nějaký druh hojný na jedné ploše, bude pravděpodobně hojný i na druhé, a díky tomu jsou početnosti druhů hojných na více dílčích plochách ve výsledku větší než při nezávislém skládání. Tím se prodlužuje „ocas“ na pravé straně rozdělení. Čistě statistické procesy tak vytvářejí rozdělení, které je mnohem šikmější a nerovnoměrnější než rozdělení normální.

Pořád ale nevíme, jestli to stačí – tedy zda je samotný proces skládání rozhodující pro výsledný tvar rozdělení populačních početností a jakou roli hraje tvar iniciálního rozdělení na začátku skládání. A tady už nám nezbývá než se uchýlit k simulacím. Ukáže se, že když máme k dispozici dostatečný počet „skládacích“ kroků, nezáleží na tom, jak iniciální rozdělení vypadalo. Je to podobné jako v případě centrálního limitního teorému, kde je lhostejno, jaká rozdělení se skládají – když jich je dost, vždy nám vyjde normální rozdělení. V našem případě nám díky nestejnému druhovému složení na sousedních plochách a prostorové autokorelaci vyjde rozdělení blízké lognormálnímu. Co je však nejdůležitější: když celý proces skládání parametrizujeme pozorovanými údaji o rozdílech v druhovém složení sousedních společenstev a o prostorové autokorelaci populačních početností, vyjdou nám rozdělení nerozlišitelná od pozorování.³⁾ Jinými slovy stačí vědět jen něco málo o prostorové struktuře společenstev, a dokážeme předpovědět, kolik procent druhů bude hojných a kolik vzácných. To něco málo jsou dvě čísla, která v sobě nesou informaci o struktuře krajiny a historii šíření druhů.

Proč je většina druhů vzácných?

S trochou nadsázky tedy můžeme na tuto otázku odpovědět tím, co jsme zmínili úplně na začátku. Je to proto, že příroda je na každém místě trochu jiná. Všude se vyskytují trochu jiné druhy, ale zároveň mají druhy na blízkých lokalitách podobné počty jedinců. Díky vzájemné hře mezi jinakostí a podobností je rozdělení, které získáme postupným skládáním sousedních ploch, čím dál šikmější a čím dál více charakterizovaný převahou vzácných druhů. Nepotřebujeme žádné speciální procesy dělby zdrojů mezi druhy; stačí, když máme rozmanitost míst. Ostatní následuje samo.

Chce se vám namítat, že by to mohlo být všechno obráceně? Že jen proto, že je většina druhů vzácná, můžeme pozorovat rozmanitost míst? Jistě, kdyby byla většina druhů hojných, byly by na většině míst a ta by si byla mnohem podobnější. Do jisté míry je opravdu otázkou vkusu, co považujeme za primární. Jenže kdyby to bylo obráceně, museli bychom najít mechanismus, který generuje vzácnost, a potíž s měřítkem a univerzalitou by se nám vrátila jako bumerang. Na jaké prostorové škále by ten zatím neznámý mechanismus fungoval? Náš příběh je mnohem jednodušší. Koneckonců si dovedeme představit spoustu důvodů, proč se místa od sebe liší (počínaje heterogenitou prostředí až po omezené schopnosti šíření jednotlivých druhů), takže právě tuto rozdílnost můžeme považovat za primární a vše ostatní za odvozené.

Je to vlastně zvláštní. Nejuniverzálnější ekologický jev, studovaný mnoho desítek let, plyne jednoduše z toho, že příroda je rozmanitá a v každém místě trochu jiná.