Na hranici biologie
 Biologové, asi stejně jako vědci z jiných oborů, nahlížejí jevy prostřednictvím nějakého interpretačního rámce, kterému se někdy říká paradigma. Nejobecnějším intrepretačním rámcem je v biologii darwinistický pohled na evoluci. Ten umožňuje hodnotit jevy (morfologické, fyziologické, etologické aj.) z hlediska jejich účelnosti (funkce), kterou můžeme vykládat prostřednictvím jejich evoluční historie, konkrétně v minulosti působícího přirozeného výběru. Vlastnost, která se lépe hodila k přežití a rozmnožování, se pochopitelně lépe předávala dalším generacím a tak se fixovala. Díky darwinistickému interpretačnímu rámci můžeme uchopit v přírodě evidentní účelnost jako cosi zákonitého a logického. Z psychologického hlediska je navíc myšlenka evoluce přírodním výběrem nesmírně přitažlivá, poněvadž nám dovoluje zařadit věci, na kterých nám v našem vlastním životě záleží nejvíc (tj. vše okolo přežití a rozmnožování), do kontextu evolučního příběhu, tedy něčeho, co se odehrává vlastně v kosmickém měřítku. Na druhou stranu tento rámec představuje past – jeho prostřednictvím si totiž můžeme snadno vysvětlit skoro všechny biologické jevy, aniž bychom se museli zamýšlet nad jejich skutečnou podstatou a povahou.
Biologové, asi stejně jako vědci z jiných oborů, nahlížejí jevy prostřednictvím nějakého interpretačního rámce, kterému se někdy říká paradigma. Nejobecnějším intrepretačním rámcem je v biologii darwinistický pohled na evoluci. Ten umožňuje hodnotit jevy (morfologické, fyziologické, etologické aj.) z hlediska jejich účelnosti (funkce), kterou můžeme vykládat prostřednictvím jejich evoluční historie, konkrétně v minulosti působícího přirozeného výběru. Vlastnost, která se lépe hodila k přežití a rozmnožování, se pochopitelně lépe předávala dalším generacím a tak se fixovala. Díky darwinistickému interpretačnímu rámci můžeme uchopit v přírodě evidentní účelnost jako cosi zákonitého a logického. Z psychologického hlediska je navíc myšlenka evoluce přírodním výběrem nesmírně přitažlivá, poněvadž nám dovoluje zařadit věci, na kterých nám v našem vlastním životě záleží nejvíc (tj. vše okolo přežití a rozmnožování), do kontextu evolučního příběhu, tedy něčeho, co se odehrává vlastně v kosmickém měřítku. Na druhou stranu tento rámec představuje past – jeho prostřednictvím si totiž můžeme snadno vysvětlit skoro všechny biologické jevy, aniž bychom se museli zamýšlet nad jejich skutečnou podstatou a povahou.
Bude proto možná vhodné všimnout si takových jevů, které do onoho paradigmatu nezapadají. Ne že by ho nějak zpochybňovaly nebo vyvracely, jsou jen zkrátka mimo. Jde o jevy, které se týkají většinou různě velkých souborů organizmů více druhů, a proto je z definice nelze vysvětlovat pomocí přirozeného výběru. Jak uvidíme, za svou nezávislost na paradigmatu tyto jevy těžce platí tím, že jsou často považovány za cosi nebiologického, za vedlejší produkt jiných (statistických, geometrických apod.) zákonitostí. Právě proto by nám ale tyto hraniční jevy mohly ukázat, o čem je biologie, co konstituuje biologické myšlení. 
Povšimněme si ale jedné skutečnosti. Fakt, že celkové rozložení početností neodráží nic biologicky relevantního, neznamená, že početnosti jednotlivých druhů jsou biologicky irelevantní. Naopak, je nanejvýš smysluplné ptát se po faktorech určujících populační početnost daného druhu, po biologických příčinách jeho početnosti. Znamená to pouze, že dohromady tyto početnosti nedávají žádný smysl, že ony určující faktory jsou buď nezávislé, anebo sice závislé, ale způsobem, který nám při tomto pohledu uniká. Situace je tedy trochu paradoxní – zatímco početnost jednotlivých druhů považujeme za biologicky velice podstatnou vlastnost, jev, jehož základem jsou vlastně tyto biologicky podstatné vlastnosti, považujeme za biologicky nezajímavý.
Ještě složitější je situace u následujícího jevu. Když seřadíme jednotlivé druhy živočichů ve společenstvu (ovšem pouze ty, které využívají podobné potravní zdroje) podle velikosti, velmi často zjistíme, že poměr velikosti těch znaků, které bezprostředně souvisí se získáváním potravy (třeba zobáků), je u jakýchkoli dvou sousedících druhů stejný a je přibližně roven číslu 1,3 (obr.Tomuto jevu byla v ekologické literatuře věnována značná pozornost a dodnes není uspokojivě potvrzeno, zda skutečně existuje, či zda vznikl v důsledku toho, že publikovány jsou pouze pozitivní výsledky. Dnes se nejčastěji tvrdí, že konstantní poměr velikosti znaků není sice obecným pravidlem, je však nápadně častý. To nás teď ale nemusí trápit. Zajímavější je spíše názor, že opět jde o biologicky irelevantní záležitost, o jakýsi matematický artefakt, o odraz nikoli biologické, ale matematické povahy skutečnosti. Autoři této myšlenky ji dokládají například zjištěním, že podobné uspořádání vykazují například některé dechové hudební nástroje (viz obr.
Kde končí biologie a začíná matematika?
V ekologii je známa spousta zajímavých korelací. Lokální početnost druhu například koreluje s velikostí jeho geografického areálu – čím má druh větší areál rozšíření, tím je lokálně početnější. To není nikterak překvapující, snad až na to, že tento jev vysvětluje několik alespoň zčásti se vylučujících teo–rií (což je ale koneckonců normální). Podobná korelace existuje mezi průměrnou populační hustotou druhu a variancí jeho hustot na různých místech, tedy čím je druh početnější, tím jsou větší i rozdíly mezi jeho početností na různých místech (obr. obrázek). Tento vztah se nazývá Taylorův zákon. Opět je sporné, zda vyjadřuje pouze matematickou zákonitost, nebo zda je zajímavý i z hlediska biologického. Samotná pozitivní korelace i linearita vztahu (v logaritmicko-logaritmickém měřítku) jsou dobře odvoditelné z teorie, lze je tedy pokládat za odraz zákonitostí matematických, vedou se ovšem diskuse, zda sklon regresní přímky není příliš velký na to, aby se dal vysvětlit pouze matematicky. V každém případě jde opět o hraniční jev, přinejmenším proto, že jakkoli může být jeho příčina čistě matematická, důsledky tohoto jevu se mohou týkat třeba rozdílné populační dynamiky různých druhů.
Tento vztah se nazývá Taylorův zákon. Opět je sporné, zda vyjadřuje pouze matematickou zákonitost, nebo zda je zajímavý i z hlediska biologického. Samotná pozitivní korelace i linearita vztahu (v logaritmicko-logaritmickém měřítku) jsou dobře odvoditelné z teorie, lze je tedy pokládat za odraz zákonitostí matematických, vedou se ovšem diskuse, zda sklon regresní přímky není příliš velký na to, aby se dal vysvětlit pouze matematicky. V každém případě jde opět o hraniční jev, přinejmenším proto, že jakkoli může být jeho příčina čistě matematická, důsledky tohoto jevu se mohou týkat třeba rozdílné populační dynamiky různých druhů.
Trochu podobná situace je u vztahu mezi velikostí plochy a počtem druhů, které na dané ploše zaznamenáme. Tento vztah je také lineární (ovšemže opět jen v tom případě, je-li na obou osách logaritmické měřítko) a tuto linearitu můžeme odvodit přímo z lognormálního rozložení početností druhů zmíněného na začátku. Poměrně dobře lze také odůvodnit, proč se sklon regresní přímky liší podle toho, zda jde o izolované plochy (ostrovy), nebo o arbitrárně vyčleněné části větší plochy. Zatím však neumíme vysvětlit, proč je sklon regresní přímky v každé z obou těchto situací takový, jaký je, proč pro různá společenstva dosahují směrnice této přímky velice podobných hodnot. Je zřejmé, že to nějak souvisí s heterogenitou prostředí, není však jasné jak. Zajímavé, nicméně neúspěšné jsou pokusy vysvětlit tento vztah fraktálovým charakterem prostředí.
Jiný případ představuje jev, který snad dokážeme vysvětlit bezezbytku, ovšem poněkud netradičním způsobem. Jde o botanikům dobře známý proces sebezřeďování, tedy snižování populační hustoty rostlin během jejich růstu. Vztah mezi populační hustotou a hmotností rostliny je lineární (opět v log-log měřítku) a můžeme jej stanovit nejen pro jeden druh, ale i mezidruhově (obr. obrázek). Kupodivu i v tomto druhém případě nám vyjde přibližně přímka, na níž leží úsečky pro jednotlivé druhy. Směrnice této přímky je -3/2, populační hustota tedy klesá pomaleji, než roste hmotnost rostlin. Zvýšení hmotnosti o tři řády vlastně znamená snížení populační hustoty pouze o dva řády. Zdá se, že vysvětlení leží přímo v geometrické povaze růstu na jedné a populační hustoty na druhé straně – zatímco hmotnost souvisí s objemem, který je třírozměrný, populační hustota je dvourozměrná. Rostlina roste do tří rozměrů, ale pouze ve dvou rozměrech na úkor okolních jedinců. Tento jev tedy představuje zvláštní případ, kdy můžeme vysvětlit na pohled biologický fenomén čistě geometricky.
Prapodivné důsledky má podobný, ale obecnější vztah mezi průměrnou hmotností jedince a průměrnou populační hustotou, sestavený pro všechny organizmy (obr. obrázek).
Kupodivu i v tomto druhém případě nám vyjde přibližně přímka, na níž leží úsečky pro jednotlivé druhy. Směrnice této přímky je -3/2, populační hustota tedy klesá pomaleji, než roste hmotnost rostlin. Zvýšení hmotnosti o tři řády vlastně znamená snížení populační hustoty pouze o dva řády. Zdá se, že vysvětlení leží přímo v geometrické povaze růstu na jedné a populační hustoty na druhé straně – zatímco hmotnost souvisí s objemem, který je třírozměrný, populační hustota je dvourozměrná. Rostlina roste do tří rozměrů, ale pouze ve dvou rozměrech na úkor okolních jedinců. Tento jev tedy představuje zvláštní případ, kdy můžeme vysvětlit na pohled biologický fenomén čistě geometricky.
Prapodivné důsledky má podobný, ale obecnější vztah mezi průměrnou hmotností jedince a průměrnou populační hustotou, sestavený pro všechny organizmy (obr. obrázek).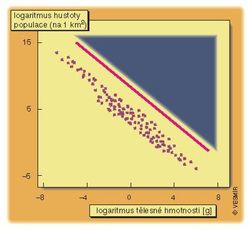 Opět není překvapivá samotná negativní korelace (je zřejmé, že slonů je méně než, dejme tomu, much), ale sklon regresní přímky. Její směrnice je totiž -0,75, což by samo o sobě nic neznamenalo, kdybychom nevěděli, že regresní přímka vztahu mezi tělesnou hmotností a spotřebou energie na jedince má směrnici +0,75. Když tedy dáme oba tyto vztahy dohromady (viz text v rámečku), abychom získali vztah mezi tělesnou hmotností a energií, kterou populace daného druhu spotřebuje na jednotku plochy, oba vztahy se vlastně „vyruší“ a zjistíme, že spotřeba energie na určité ploše na tělesné hmotnosti nezávisí. Populace slonů na 10 km2 spotřebuje přibližně stejné množství energie jako populace much na stejné ploše. Toto zjištění se nazývá pravidlo energetické ekvivalence a patří k největším podivnostem v ekologii.
Opět není překvapivá samotná negativní korelace (je zřejmé, že slonů je méně než, dejme tomu, much), ale sklon regresní přímky. Její směrnice je totiž -0,75, což by samo o sobě nic neznamenalo, kdybychom nevěděli, že regresní přímka vztahu mezi tělesnou hmotností a spotřebou energie na jedince má směrnici +0,75. Když tedy dáme oba tyto vztahy dohromady (viz text v rámečku), abychom získali vztah mezi tělesnou hmotností a energií, kterou populace daného druhu spotřebuje na jednotku plochy, oba vztahy se vlastně „vyruší“ a zjistíme, že spotřeba energie na určité ploše na tělesné hmotnosti nezávisí. Populace slonů na 10 km2 spotřebuje přibližně stejné množství energie jako populace much na stejné ploše. Toto zjištění se nazývá pravidlo energetické ekvivalence a patří k největším podivnostem v ekologii.
Když se ale na obr. obrázek podíváme pořádně, můžeme snadno začít pochybovat o oprávněnosti zmíněných interpretací. Výsledný obraz lze totiž přinejmenším zčásti vykládat jako důsledek čistě fyzikálních omezení – trojúhelník v pravém horním rohu představuje „zakázanou oblast“, v níž by organizmy byly už tak velké a zároveň tak nahusto, že by se už do prostoru vůbec nevešly. Vlevo dole by zase přinejmenším sexuálně se rozmnožující organizmy měly značné problémy se vůbec najít (nemluvě o tom, že takto malé a zároveň řídce se vyskytující organizmy pravděpodobně nemohli nalézt ani výzkumníci, na základě jejichž dat výsledný obraz vznikl). Zjištěná „závislost“ tedy nemusí vůbec zachycovat opravdovou závislost, může být pouze vedlejším produktem zmíněných omezení. Všimněme si navíc, že rozptyl hodnot v daném vztahu dosahuje několika řádů a měřítka, ve kterých se pohybujeme díky logaritmické stupnici, jsou tak obrovská, že naše přirozená intuice, která nás obvykle vede při hodnocení podobných vztahů, musí nutně selhat. Těžko tedy říci, co si o tomto vztahu máme myslet.
Potravní řetězce většiny společenstev mají relativně málo článků, nejčastěji 3 – 4. Řetězce delší než 6 článků už jsou velice vzácné. Tradiční vysvětlení je založeno na důsledcích druhého termodynamického zákona, konkrétně na známé skutečnosti, že energetické ztráty na každé potravní úrovni představují 80 – 90 % volné energie. Organizmy na vyšší potravní úrovni tak mají k dispozici pouze 10 – 20 % původní volné energie. Živočichové představující koncové články potravních řetězců tedy mají k dispozici tak málo energie, že taktak udrží populaci dostatečně velkou, aby mohla existovat dlouhodobě. Jinými slovy, protože každá potravní úroveň může využívat jen asi 10 % energie dostupné pro úroveň nižší, pro nejvyšší potravní úrovně zbude tak málo energie, že už se neuživí dostatečně velký počet jedinců, který by zajistil dlouhodobé přežívání populace.Toto elegantní učebnicové vysvětlení není tak úplně neproblematické. Kdyby například termodynamické vysvětlení mělo všebecnou platnost, desetkrát vyšší celková produktivita prostředí (tedy celkový přísun energie do společenstva, který se mezi jednotlivými typy prostředí na Zemi mnohdy liší až o tři řády) by měla za následek prodloužení průměrného potravního řetězce o jeden článek. Protože tomu tak není, byla vytvořena alternativní teorie, která tvrdí, že delší potravní řetězce jsou nestabilní a časem se zhroutí. Matematické modely to skutečně potvrdily, ovšem těžko posoudit, jaká je jejich výpovědní hodnota.
Fenoménů podobného druhu je řada. Všechny cosi vypovídají o světě, my ale často nevíme co, poněvadž je nedokážeme dost dobře zařadit do běžných interpretačních rámců. Jejich podstata leží vždy alespoň zčásti mimo biologii, proto budí u mnoha biologů nedůvěru. Na druhou stranu, hlubší podstata i výsostně biologických jevů leží vlastně mimo – tvary živých struktur jsou například dány do značné míry geometrickými a fyzikálními omezeními, stejně jako třeba dynamika růstu. Dokonce i tak „biologický“ jev, jako je přírodní výběr, se řídí zákonitostmi populační genetiky, jež jsou vlastně matematické. Nakonec totiž každá důsledná interpretace biologických jevů musí zasahovat za hranice biologie. Možná to souvisí s tím, že fenomén života je sám o sobě neuchopitelný.Tvrzení, že směrnice regresní přímky je –0,75, znamená, že regresní přímku můžeme vyjádřit rovnicí y = –0.75x + b (b je konstanta, která nás nemusí zajímat). Vzhledem k tomu, že na ose x je logaritmus hmotnosti organizmu (W) a na ose y logaritmus populační hustoty (D), můžeme vztah vyjádřit rovnicí
logD = 0,75logW + log k
a po odlogaritmování
D = kW-0,75
Podobně vztah mezi hmotností a spotřebou energie je
E = tW+0,75
(t je opět konstanta)
Chceme-li vyjádřit, kolik energie prochází danou plochou v závislosti na hmotnosti organizmu, musíme vynásobit energii, kterou spotřebuje jeden jedinec (E) počtem jedinců na dané ploše, tedy populační hustotou (D). Potom
D×E = kW-0,75 × tW+0,75 = kt
Energie, která prochází populací na dané ploše, tedy nezávisí na tělesné hmotnosti jedinců.
O autorovi
David Storch


























