Kvantové hlavolamy I
| 5. 3. 1998Hamlet: Vidíte tamten mrak? Že vypadá jako velbloud?
Polonius: Na mou věru, dočista jako velbloud.
Hamlet: Řekl bych, že jako lasička.
Polonius: Záda to má jako lasička.
Hamlet: Či jako vorvaň?
Polonius: Úplně jako vorvaň.
W. Shakespeare, Hamlet (v překladu E. A. Saudka)
Kvantová teorie je dnes asi nejlépe testovaná fyzikální teorie vůbec. Potvrzuje ji obrovské (a každý den narůstající!) množství experimentálních dat z nejrůznějších oborů fyziky – optiky, fyziky kondenzované fáze, fyziky atomů, jader a elementárních částic… Přestože kvantové zákony poznáváme již téměř sto let, jejich podstata nás dodnes nepřestává udivovat. Umíte si třeba představit, že jeden foton může současně procházet různými dráhami, ale přitom se při každém měření dá nachytat jen na jedné z nich?
Kvantové skoky
Asi nejznámějším projevem kvantové mechaniky, z něhož se odvozuje i její jméno, je kvantování fyzikálních veličin. Tím označujeme skutečnost, že fyzikální veličiny mají, na rozdíl od klasické (tj. předkvantové) fyziky, nespojitý (diskrétní) charakter. Např. energie elektronu v atomu vodíku nabývá jen některých hodnot, které po vynesení na číselnou osu tvoří posloupnost vzájemně oddělených bodů; všechny ostatní hodnoty jsou „zakázány“. Kvantování energie najdeme kromě atomů také v krystalových mřížkách, molekulách, atomových jádrech, soustavách vázaných kvarků a mnoha jiných mikroskopických systémech.O kvantování se vědělo vlastně již od počátku našeho století, kdy Albert Einstein a Max Planck ukázali, že výměna energie mezi elektromagnetickým zářením a látkou se (při dané frekvenci záření) uskutečňuje jen po celistvých násobcích jistých minimálních porcí. To je způsobeno kvantováním energie elektronů v atomech a zároveň existencí „kvant“ elektromagnetického záření, fotonů. Mezi první, kdo se fenomén kvantování pokoušeli vysvětlit, patřili Niels Bohr a Arnold Sommerfeld. Podle nich se elektrony v atomech mohou pohybovat jen po určitých orbitách, jimž právě odpovídají výše zmíněné diskrétní energie. Tato teorie však byla jen jakýmsi nouzovým vysvětlením toho, že atomy jsou stabilní navzdory klasické elektrodynamice, podle níž atomární elektrony mají „padat“ do atomového jádra v důsledku ztráty energie vyzařováním. Teprve v roce 1926 publikoval Erwin Schrödinger sérii článků s názvem Kvantování jako problém vlastních hodnot, v nichž jsou principy kvantování vyloženy deduktivním způsobem, nikoliv pouze fenomenologicky. Spolu s asi o rok staršími pracemi Wernera Heisenberga je pokládáme za základ současné podoby kvantové mechaniky.
 Podle původních Bohrových představ mohou stavy atomu prodělávat jen skokové změny (přechody mezi jednotlivými kvantovými stavy za současného vyzáření fotonu odpovídající energie). Schrödinger viděl hlavní význam své práce v tom, že se v ní diskrétní energetická spektra atomů a náhlé kvantové přechody ukázaly být důsledkem matematicky jasných postulátů kladených na jistou spojitou a plynule se vyvíjející funkci polohy elektronu, tzv. vlnovou funkci. Ukázalo se ale, že ani to k zažehnání kvantových diskontinuit nestačí. Vypráví se 1) , že po jedné z celodenních diskusí s Bohrem Schrödinger vykřikl: Jestliže budeme muset jít dál s těmi prokletými kvantovými skoky, pak lituji, že jsem se do toho kdy míchal. Bohr odpověděl: Ale my ostatní jsme vám za to velmi vděčni, protože vaše práce udělala pro zdokonalení této teorie mnoho. Vlnová funkce a s ní související fyzika skutečně přinesly do našeho chápání přírody (ale i do chápání mezí tohoto chápání) tak zásadní změny, že diskuse o jejich důsledcích dosud pokračuje. Podívejme se, v čem tyto změny spočívají 2) .
Podle původních Bohrových představ mohou stavy atomu prodělávat jen skokové změny (přechody mezi jednotlivými kvantovými stavy za současného vyzáření fotonu odpovídající energie). Schrödinger viděl hlavní význam své práce v tom, že se v ní diskrétní energetická spektra atomů a náhlé kvantové přechody ukázaly být důsledkem matematicky jasných postulátů kladených na jistou spojitou a plynule se vyvíjející funkci polohy elektronu, tzv. vlnovou funkci. Ukázalo se ale, že ani to k zažehnání kvantových diskontinuit nestačí. Vypráví se 1) , že po jedné z celodenních diskusí s Bohrem Schrödinger vykřikl: Jestliže budeme muset jít dál s těmi prokletými kvantovými skoky, pak lituji, že jsem se do toho kdy míchal. Bohr odpověděl: Ale my ostatní jsme vám za to velmi vděčni, protože vaše práce udělala pro zdokonalení této teorie mnoho. Vlnová funkce a s ní související fyzika skutečně přinesly do našeho chápání přírody (ale i do chápání mezí tohoto chápání) tak zásadní změny, že diskuse o jejich důsledcích dosud pokračuje. Podívejme se, v čem tyto změny spočívají 2) .
Interference jednoho fotonu
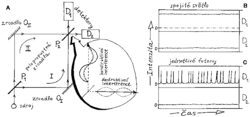
Uvažujme jednoduchý optický přístroj, tzv. Machův–Zehnderův interferometr, na obrázku A. Paprsek světla ze zdroje dopadá na polopropustné zrcadlo P1, které polovinu intenzity propouští a polovinu odráží, takže dopadající paprsek štěpí na paprsky dva. Každý z nich prochází jedním ramenem interferometru (I či II), odráží se od obyčejného zrcadla OI nebo OII, aby dospěl k polopropustnému zrcadlu P2 (opět s rovným poměrem dělení intenzit), kde se sbíhá s druhým paprskem. Interferometr je navržen tak, že optické dráhy paprsků v obou ramenech jsou přesně stejné. Za jistých podmínek se světlo za zrcadlem P2 šíří pouze ve směru paprsku z větve I, tedy nahoru. Detektor D1 pak registruje veškerou intenzitu, zatímco detektor D2 neregistruje intenzitu žádnou (viz obrázek B).Tento jev je učebnicovým příkladem tzv. interference světla, dokládajícím jeho vlnovou povahu (světlo je elektromagnetické vlnění). Geometrickou představu paprsků musíme nahradit představou světelných vln šířících se rameny interferometru. Prvky interferometru lze udělat tak, že při průchodu polopropustným zrcadlem vlna plynule pokračuje, zatímco při každém odrazu dochází k jejímu posunu o čtvrtinu periody (tj. o čtvrtinu vlnové délky). Světlo dopadající do každého z detektorů se skládá z dvojice vln prošlých oběma rameny, které se sčítají do vlny výsledné. Obě vlny dopadající do D1 se na své cestě odrazily dvakrát. Jejich vzájemný posun je tedy nulový, takže se sčítáním zesilují (nastává konstruktivní interference). U detektoru D2 vlna prošlá ramenem I prodělala tři odrazy, zatímco vlna z ramene II pouze jeden. Jejich vzájemný posun je proto roven polovině periody, obě vlny jsou tedy v protifázi a v součtu dají nulu (destruktivní interference) 3) – viz obrázek.
Již jsme se zmínili o tom, že podle moderní fyziky je světlo proud kvant, tzv. fotonů. Obvyklé zdroje vyzařují tak obrovské počty fotonů za vteřinu, že nespojitá povaha jejich světla není patrná. V takových případech dobře funguje klasická vlnová teorie. Intenzitu světelného zdroje lze ale snížit až do té míry, že detektory za zrcadlem P2 pouze tu a tam registrují impulz, odpovídající jedinému dopadlému fotonu (pro jednoduchost budeme předpokládat stoprocentní účinnost registrace fotonů oběma detektory) – viz obrázek C. Budeme-li postupně zeslabovat intenzitu světla, zjistíme, že interferenční chování pozorované při vyšších intenzitách, tj. fakt, že světlo dopadá pouze na detektor D1, se při tom nemění. Viděli jsme, že klíčem pro pochopení interference při vyšších světelných intenzitách je vlnová představa, v níž se světlo šíří zároveň oběma větvemi interferometru. Jak ale vysvětlit interferenci pro jediný foton, jehož současnou přítomnost v obou ramenech interferometru si neumíme představit? Jednoduchý předpoklad, že na polopropustných zrcadlech se foton s pravděpodobností 50 % odrazí a s pravděpodobností 50 % projde, zjevně nepostačuje, neboť připouští i takový vývoj, při němž se foton na obou polopropustných zrcadlech odrazí, či naopak na obou projde, což by vedlo k jeho registraci detektorem D2, tedy k rozporu s experimentem.
Potíž je v tom, že představa částice (fotonu) jako dobře prostorově lokalizovaného objektu, který se nemůže vyskytovat zároveň na dvou odlišných místech, je pozůstatkem „klasického“ myšlení, jež v kvantovém světě neplatí. Abychom vysvětlili interferenční chování jednotlivých fotonů v našem experimentu, musíme se této představy vzdát a připustit, že jeden foton se opravdu může šířit oběma rameny současně. (To že dělají? Fuj!) Jak uvidíme dále, podle kvantové teorie je stav fotonu za zrcadlem P1 dán tzv. superpozicí obou možných alternativ šíření, tj. průchodu větví I a průchodu větví II.
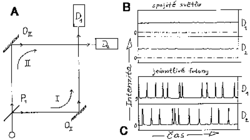 To však ještě není všechno. Představme si nyní, že z našeho optického přístroje odstraníme polopropustné zrcadlo P2 (viz obrázek A). Interference pak samozřejmě zmizí – fotony budou dopadat jak do detektoru D1, tak do D2 (obrázek B). Jestliže se jediný foton, jak jsme řekli, šíří oběma rameny současně, pak bychom mohli očekávat, že bude registrován oběma detektory zároveň. Chyba lávky! Ve skutečnosti jediný foton může být zaregistrován pouze jedním detektorem – je nedělitelný, tj. nelze zaregistrovat něco jako „půlku fotonu“ (obrázek C). Jak je to ale možné? To se teď foton pro změnu šíří jen jedním ramenem?
To však ještě není všechno. Představme si nyní, že z našeho optického přístroje odstraníme polopropustné zrcadlo P2 (viz obrázek A). Interference pak samozřejmě zmizí – fotony budou dopadat jak do detektoru D1, tak do D2 (obrázek B). Jestliže se jediný foton, jak jsme řekli, šíří oběma rameny současně, pak bychom mohli očekávat, že bude registrován oběma detektory zároveň. Chyba lávky! Ve skutečnosti jediný foton může být zaregistrován pouze jedním detektorem – je nedělitelný, tj. nelze zaregistrovat něco jako „půlku fotonu“ (obrázek C). Jak je to ale možné? To se teď foton pro změnu šíří jen jedním ramenem?
Bránící se rozum
Výše popsané jevy jsou dnes již dobře prokázaným experimentálním faktem 4) a zdá se, že je nelze opatřit žádným „klasickým“, „zdravému rozumu“ pochopitelným vysvětlením. Mohli bychom se třeba domnívat, že foton se před vstupem do interferometru nějak „dozví“ o přítomnosti či nepřítomnosti zrcadla P2 a „vybere“ si podle toho jednu ze dvou alternativ svého chování: buď se šíří zároveň oběma rameny jako klasická vlna (měření s P2), nebo si zvolí pouze jedno rameno jako klasická částice (měření bez P2). Představme si ale, že rozhodnutí o umístění či neumístění zrcadla P2 do cesty fotonu je učiněno teprve v poslední nanosekundě před jeho průchodem místem P2. Za tuto dobu světlo uletí jen asi 30 cm. Pokud je délka ramen větší, bude tedy foton určitě za vstupním zrcadlem P1, takže svou volbu již nemůže změnit. Přesto je podle kvantové teorie výsledek pokusu nezávislý na tom, zda rozhodnutí o zrcadle P2 bylo učiněno dlouho před měřením, či až v posledním okamžiku. Nedá se nic dělat, s klasickou logikou jsme zde prostě v koncích!Právě popsaný experiment se zpožděnou volbou navrhl r. 1978 John Archibald Wheeler a v poněkud modifikované podobě jej uskutečnili r. 1986 na univerzitách v Mnichově a Marylandu. Místo mechanického ovládání zrcadla P2 (které by v tak krátkých časech nebylo technicky proveditelné) byl do jednoho ramene interferometru vložen ultrarychle (tj. v nanosekundových časech) aktivovatelný optický element, umožňující zjistit přítomnost fotonu v tomto rameni. Předpovědi kvantové teorie v tomto i dalších podobných pokusech byly zcela potvrzeny.
Musíme tedy přijmout jako fakt, že při měření interference (tj. se zrcadlem P2) je foton „vlnou“, zatímco při měření dráhy (tj. bez P2) je týž foton „částicí“. Toto dvojaké chování je příkladem obecné vlastnosti kvantového světa, které se často říká vlnově-částicový dualizmus (viz také J. Podolský, Vesmír 71, 193, 1992/4). Fotony (a jak uvidíme dále, i další částice) mají zkrátka dvě tváře (podobně jako Dr. Jekyll alias Mr. Hyde), které se jakoby vzájemně doplňují – jsou komplementární.
Na cestě k pochopení kvantových jevů se navíc musíme vzdát i tak významného atributu klasické fyziky, jakým je její striktní determinizmus. V bezinterferenčním uspořádání je totiž podle kvantové mechaniky principiálně nemožné předpovědět, do jakého z detektorů foton dopadne; pro obě alternativy lze stanovit pouze pravděpodobnosti. Zdá se tedy, že náhoda je jaksi „vtištěna“ do základů našeho světa.
N. Bohr, spolutvůrce kvantové teorie a její brilantní advokát v diskusích s A. Einsteinem 5) , se důsledky kvantových zákonů pro naše myšlení a vidění světa snažil převést do srozumitelného jazyka. V jeho pojetí kvantový svět ponechává mnoho svých vlastností neurčitých a obsahuje tak velké bohatství různých alternativ. My, makroskopičtí tvorové, se tyto vlastnosti snažíme dobýt pomocí klasických měřicích přístrojů, a proto dospíváme ke zdánlivě neslučitelným a ne přesně předpověditelným výsledkům. Samotný akt měření se přitom stává podstatným účastníkem fyzikálních dějů. J. A. Wheeler shrnuje Bohrovy úvahy takto: Žádný elementární jev není jevem, dokud není registrovaným (pozorovaným) jevem […] dokud není doveden do konce nevratným aktem zesílení, jakým je zčernání zrna bromidu stříbra ve fotografické emulzi nebo spuštění impulzu fotodetektoru. Jak uvidíme příště, matematickým vyjádřením bohatství možností skrývajících se v kvantovém světě je princip superpozice, zatímco pravděpodobnostní vydělení výsledné podoby se děje v procesu kvantového měření.
Poznámky
Kvantování energie kyvadla
Kvantová teorie je univerzální, a proto se kvantování týká i makroskopických objektů. Zde jsou však jeho projevy tak subtilní, že odchylky od klasické mechaniky téměř nepozorujeme. Představme si třeba jednoduché kyvadélko: Kulička zavěšená na velmi lehkém závěsu je gravitační silou donucena vykonávat kmity kolem své rovnovážné polohy. Energie takových kmitů (tj. maximální kinetická energie kývající se kuličky) nabývá typicky hodnot řekněme desetitisícin joulu (1 J je asi 0,239 kalorie) např. při délce závěsu 20 cm, maximální výchylce ze svislé polohy 5o a hmotnosti kuličky 20 gramů je energie kmitů v zemském tíhovém poli rovna asi 1,5×104 J. Podle klasické mechaniky můžeme tuto energii měnit spojitě (stačí nepatrně změnit počáteční výchylku nebo impulz kuličky), ve skutečnosti se však i zde uplatňuje kvantování. Jednotlivé energetické hladiny jsou ale vzdáleny jen o zhruba 1033 J, což je hodnota z makroskopického hlediska zcela nicotná (je např. silně přehlušena i nepatrným termickým chvěním kyvadélka, jehož energie je při běžných teplotách řádu 1021 J, tedy asi bilionkrát větší). V důmyslných experimentech se ale kvantování podařilo prokázat nejen na mikroskopické, ale i na makroskopické úrovni.
Astronomická verze interferenčního pokusu
J. A. Wheeler ukázal, že experiment se zpožděnou volbou se dá provést také v poněkud větším měřítku, dávajícím bizarnosti kvantového dualizmu snad ještě více vyniknout. Nedávno bylo totiž zjištěno, že dva astronomické objekty s označením 0957+561A a 0957+561B, oddělené úhlovou odchylkou 6″, 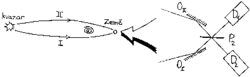 jsou ve skutečnosti obrazem jediného astrofyzikálního útvaru (kvazaru). Ke zdvojení jeho obrazu dochází gravitačním rozštěpením dráhy fotonů působením galaxie, nacházející se asi na čtvrtině cesty od Země ke kvazaru (viz obrázek). Obě rozštěpené větve šíření světla tvoří vlastně dvě ramena pomyslného interferometru. Protože doba putování fotonů od kvazaru k Zemi je několik miliard let, mohlo by být rozhodnutí o umístění či neumístění zrcadla P2 do cesty fotonům pohodlně učiněno v lidských časových měřítkách (např. při ranní kávě).
jsou ve skutečnosti obrazem jediného astrofyzikálního útvaru (kvazaru). Ke zdvojení jeho obrazu dochází gravitačním rozštěpením dráhy fotonů působením galaxie, nacházející se asi na čtvrtině cesty od Země ke kvazaru (viz obrázek). Obě rozštěpené větve šíření světla tvoří vlastně dvě ramena pomyslného interferometru. Protože doba putování fotonů od kvazaru k Zemi je několik miliard let, mohlo by být rozhodnutí o umístění či neumístění zrcadla P2 do cesty fotonům pohodlně učiněno v lidských časových měřítkách (např. při ranní kávě).
Ke stažení
 Článek ve formátu PDF [146,2 kB]
Článek ve formátu PDF [146,2 kB]
















