Aktuální číslo:

Kvantové hlavolamy II.

Jednofotonová interference a základy kvantové mechaniky

| 5. 4. 1998

| Vesmír 77, 189, 1998/4

| Seriál: Kvantové hlavolamy, 2. díl (Předchozí – Následující)

Stavy kvantových částic mají zvláštní vlastnosti: Např. elektron, když se na něj zrovna „nedíváme“, nemá žádnou konkrétní polohu, ale naopak v jistém smyslu je na všech místech současně. V kvantové mechanice se totiž stav částice popisuje vlnovou funkcí, která každému bodu prostoru přiřazuje určité komplexním číslo. I když vlnová funkce je pro popis toho, co se s částicí děje, naprosto nezbytná (např. umožňuje vysvětlit interferenční jevy), nemůžeme ji přímo měřit. Měření polohy pokaždé vede k výsledku, že částice v určitém místě (části prostoru) buď je, nebo není. Vlnová funkce určuje pouze pravděpodobnosti těchto výsledků.

Princip superpozice

Zásadní význam pro každou fyzikální teorii má pojem „stav systému“. Každý intuitivně chápe, že nějaký objekt může být v různých stavech a je to přitom stále týž objekt, např. káva může být horká nebo studená, automobil jedoucí nebo stojící atp. Ve fyzice je pojem stavu vyjádřen matematicky. Každá fyzikální teorie totiž přiřazuje reálným stavům zkoumaného systému prvky (body, vektory) nějakého abstraktního prostoru a s těmi potom pracuje. Například v klasické mechanice je stav bezstrukturní částice ve vnějším silovém poli určen trojicí polohových souřadnic částice r=(r_x,r_y,r_z) [mluvíme o vektoru polohy] a trojicí složek její hybnosti p=(p_x,p_y,p_z) [vektor hybnosti je úměrný rychlosti v částice: p=mv, kde m je hmotnost]. Znalost těchto šesti veličin v daném okamžiku při určeném silovém poli dostačuje nejen ke stanovení libovolné další veličiny charakterizující částici (např. energie), ale i k výpočtu všech budoucích (a díky vratnosti zákonů klasické mechaniky i minulých) poloh a hybností. Všechny stavy klasické částice jsou tedy popsány všemi možnými dvojicemi vektorů r a p.

Aby bylo možné popsat jednočásticové interferenční jevy, jako například ten z minulého čísla Vesmíru (viz rámeček 1 ), doznal popis stavů v kvantové fyzice zásadních změn. Dokonce pro něj byla vymyšlena zvláštní symbolika. Stavy kvantových systémů se ve fyzikálním textu většinou označují speciálními závorkami, |>, do nichž se vpisují buď fyzikální charakteristiky daného stavu (např. energie E), nebo v obecném případě řecká písmena (nejoblíbenější jsou velké a malé psí – Ψ a ψ) či jiné symboly.

Jednou z odlišností, které kvantová mechanika do chápání stavu fyzikálního systému přinesla, je to, že podle slavných relací neurčitosti, odvozených již W. Heisenbergem, nelze kvantové částici přiřadit polohu i hybnost současně. Můžeme tedy mluvit pouze o částici v místě r (její stav označíme symbolem |r>) nebo o částici s hybnostíp (stav |p>), ale nikdy o částici v místě r s hybností p.

Tou hlavní novinkou v kvantovém pojetí stavů, kterou se teď chceme zabývat, je kombinování dvou či více stavů ve stavy nové podle principu superpozice: jestliže se částice může nacházet v místě r₁, tj. ve stavu |r₁>, nebo v místě r₂, tj. stavu |r₂>, pak lze připravit i stavy α|r₁>+β|r₂>, kde α a β jsou libovolné číselné koeficienty. Co to znamená? Stav α|r₁>+β|r₂> není obecně totožný s |r₁> či |r₂>, ani s žádným jiným polohovým stavem |r₃> (např. ani se stavem odpovídajícím místu r₃=αr₁+βr₂). Nepopisuje totiž vůbec částici v jednom určitém místě prostoru (viz obrázek). V kvantové fyzice se pro takové stavy používá termín superpozice ¹⁾ (viz rovněž Vesmír 76, 250, 1997/5).

Každý kvantový systém se pochopitelně s časem vyvíjí – jeho stav se může měnit. Mluvíme o evoluci systému. Při ní zůstávají stavy superpozice vždy zachovány. To znamená, že stav α|φ₀>+β|Ω₀> po uběhnutí libovolného času t zůstane superpozicí α|φ_t>+β|Ω_t> stavů |φ_t> a |Ω_t>, ve které by se vyvinuly původní stavy |φ₀> a |Ω₀> samotné. Tato vlastnost kvantových evolučních rovnic se nazývá linearita.

Koeficienty v superpozicích (třeba α a β) nemusí být pouze reálná čísla, na něž jsme zvyklí z obyčejného počítání, ale jsou jimi obecně čísla komplexní (viz rámeček 2 ). Zatímco absolutní hodnota (přesněji její kvadrát) komplexního koeficientu u daného členu superpozice určuje jakousi váhu, míru významnosti tohoto členu v celkovém stavu, fáze tohoto koeficientu nemá klasickou interpretaci. Právě tato fáze však odpovídá za interferenční chování.

Interference jednoho fotonu

Princip superpozice, aritmetika komplexních čísel a linearita kvantové evoluce jsou klíčovými prvky vysvětlení podivného chování fotonů v interferometru na obrázku A obrázek. Budeme rozlišovat dva základní stavy: |↑> je stav fotonu pohybujícího se směrem „nahoru“, |→> je stav fotonu letícího „doprava“ (víme, že pouhý směr šíření stav fotonu plně nespecifikuje, ale toto zjednodušení lze teď připustit). Foton přicházející od zdroje k polopropustnému zrcadlu P1 je ve stavu |↑>. Za polopropustným zrcadlem je stav fotonu superpozicí původního směru šíření (foton prošel zrcadlem) a směru kolmého (foton se odrazil). Již víme, že odražená vlna se v našem případě posouvá o čtvrtinu periody. Kvantovou analogií tohoto faktu je, že složka superpozice odpovídající odrazu je vynásobena imaginární jednotkou ²⁾ i. Za zrcadlem P₁ je tedy stav fotonu vyjádřen jako |↑> + i|→>. Právě tato superpozice dává matematický obsah tvrzení, že jediný foton se šíří oběma rameny současně.

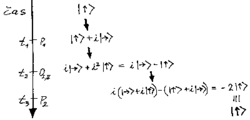K další změně stavu fotonu dojde v okamžiku společného odrazu na zrcadlech O_I a O_II (dráhy v obou ramenech jsou stejné). Přitom se první složka uvažované superpozice mění na i|→>, druhá na i²|↑>=–|↑> (v obou případech jsme stavy násobili imaginární jednotkou, protože došlo k odrazu). Po odrazech tedy máme i|→>–|↑>.

V bezinterferenčním uspořádání bez polopropustného zrcadla P₂ je tento stav konečným stavem fotonu po průchodu přístrojem. V interferenčním uspořádání se ale na P₂ první člen poslední superpozice mění na i|→> –|↑> a druhý člen (včetně znaménka minus) na -i|→> – |↑> (viz obrázek). Sečtením obou členů dostaneme výsledek –2|↑>.

Nyní jsme sice dosáhli vymizení stavu |→> fotonu šířícího se do detektoru D₂, ale ke stavu |↑> fotonu směřujícího do detektoru D₁ se dostal podivný faktor –2. Ve skutečnosti –2|↑> znamená totéž jako |↑>. Obecně totiž platí, že výraz α|→>+β|↑> vynásobený libovolným číslem popisuje stále týž fyzikální stav systému ³⁾ .

Postup, který jsme právě popsali, je kvantově-mechanickým vysvětlením interferenčního chování fotonů v Machově-Zehnderově interferometru. Zdůrazněme, že jsme po celou dobu pracovali se stavem jediného fotonu. Vše zůstane v platnosti i tehdy, je-li zrcadlo P₂ v experimentu se zpožděnou volbou (viz Vesmír 77, 129, 1998/3) umístěno do cesty fotonu až na poslední chvíli.

Superpozice kolem nás

To, že kvantová teorie vysvětluje jednofotonovou interferenci, má velmi závažné důsledky. Foton je totiž částice jako každá jiná (byť má nulovou klidovou hmotnost), a proto by měl princip superpozice určovat i chování elektronů a dalších částic. Elektronové interferenční jevy byly skutečně objeveny již r. 1927 při rozptylu na krystalech. Zjistilo se, že intenzita toku rozptýlených elektronů vykazuje maxima a minima pro určité, na energii elektronů závisející úhly odklonu od rovin krystalu. Máme zde opět co činit s jevem analogickým tomu, co pozorujeme v našem optickém interferometru – vlny se v některých směrech sčítají „konstruktivně“, v jiných „destruktivně“.

Vlnové vlastnosti hmotných částic jsou popsány Schrödingerovou vlnovou funkcí Ψ(r) – viz rámeček 3 . Rozptylové experimenty s neutrony dnes běžně slouží k určování struktury krystalických látek. Na kvantové interference jsou zvyklí také jaderní a částicoví fyzikové, kteří vnitřní strukturu atomových jader a subjaderných částic zkoumají pomocí srážek a rozptylů s využitím urychlovačů (příklad v rámečku 3 ). Kromě toho již byly provedeny jednočásticové interferenční pokusy s neutrony a připravují se i částicové verze experimentů se zpožděnou volbou.

Kvantové chování jednotlivých fotonů způsobuje, že i velké soubory fotonů, vyzařované klasickými světelnými zdroji, mají vlnové vlastnosti. Proto vlnová teorie světla již počátkem 19. století zvítězila nad teorií korpuskulární. V myšlení fyziků zdomácněla natolik, že elektromagnetické pole rozprostřené v prostoru (s rovnicemi majícími „vlnová řešení“) se koncem století mohlo stát rovnoprávnou součástí fyzikálního světa – vedle lokalizovaných hmotných částic podléhajících Newtonovým zákonům. Objev kvantování vzápětí zamíchal karty: vždyť elektromagnetické pole jsou vlastně také „částice“, a skutečné částice mají naopak vlastnosti „pole“. Dnešní kvantová teorie pole mluví stejným jazykem o všech „kvantech“, ať už jde o fotony, elektrony, kvarky či třeba gluony.

Proč vlnové vlastnosti snadno pozorujeme u velkých souborů fotonů, ale ne u běžně dostupných souborů hmotných částic? Odpověď na tuto otázku není vůbec jednoduchá. Interference obyčejného světla je vlastně důsledkem toho, že mnoho fotonů se dokáže chovat „jako jeden“, a přitom se po dlouhou dobu udržet v tzv. čistém kvantovém stavu ⁴⁾ (nebo aspoň ve stavu, který se čistému blíží). Připravit čistý stav souboru velkého počtu hmotných částic je mnohem těžší, protože částice zpravidla intenzivně interagují se svým okolím a tím se jejich stav velmi rychle porušuje. V určitých situacích (obvykle za velmi nízkých teplot) je ale možné částicové interferenční jevy pozorovat i na makroskopické úrovni. Např. vymizení elektrického odporu (viskozity) supravodivých (supratekutých) látek a jejich další neobvyklé vlastnosti jsou přímým důsledkem kvantového chování mikroskopických částic. Tak je možné pomocí supravodivého obvodu s dvěma paralelně zapojenými Josephsonovými spoji vytvořit supravodivou analogii našeho optického interferometru. Kvantové interference zde vykazují makroskopicky měřitelné proudy protékající oběma spoji!

Kvantové měření

Vraťme se teď zase k našim jednofotonovým pokusům (viz rámeček ). Zatím jsme viděli, jak se jednofotonový interferenční jev v uspořádání podle obr. A vysvětluje na základě principu superpozice. Skutečnost, že v bezinterferenčním uspořádání podle obrázku B je foton registrován náhodně vždy pouze jedním detektorem, souvisí s dalším důležitým principem kvantové teorie, představovaným pojmem kvantové měření.

V klasické fyzice měření prostě jen zjišťuje stav sledovaného objektu. Z výsledku měření lze usoudit, v jakém stavu se objekt nacházel bezprostředně před měřením (a v ideálním případě také bezprostředně po něm). Důvod, proč tento přístup musel být v kvantové mechanice opuštěn, je zjevný: Výsledek každého fyzikálního měření prováděného na libovolném stavu Ψ je vyjádřen pouze jednou naměřenou hodnotou příslušné veličiny, zatímco stav Ψ může být superpozicí stavů odpovídajících několika různým hodnotám. Prostor stavů obsahující kvantové superpozice je tak bohatší než množina možných výsledků měření.

Co se děje při kvantovém měření, si popíšeme na jednoduchém příkladu měření energie elektronu v atomu vodíku. Omezíme se na případy, v nichž se elektron nachází v libovolné superpozici pouze dvou povolených energetických stavů |Ε₁> a |Ε₂> odpovídajících energiím E1 a E2. Je jasné, že měření na stavu |Ε₁>, resp. |Ε₂> povede s jistotou k výsledkům E1, resp. E2. ⁵⁾ Co ale bude výsledkem měření, když elektron uvedeme (např. působením vnějšího elektromagnetického pole indukujícího přechody mezi oběma hladinami) do stavu |Ω>=α|Ε₁> + α|Ε₂>? Můžeme si představit, že |Ε₁> a |Ε₂> jsou dva sousední povolené energetické stavy, takže v žádném případě nesmíme naměřit (jak bychom mohli naivně předpokládat) „něco mezi E1 a E2“ (tato hodnota by ležela v „zakázaném pásu“ energií). Výsledkem může být buď E1, nebo E2, nic jiného. Kvantová teorie nepředpovídá, která z těchto dvou hodnot bude v daném měření zjištěna; to je podle ní náhodné. Předpovídá však pravděpodobnosti odpovídající oběma alternativám. Ty jsou úměrné druhým mocninám absolutních hodnot koeficientů α a β v kvantové superpozici |Ω>, tedy hodnotě |α|² pro energii E1 a |β|² pro E2. ⁶⁾

Teď konečně můžeme dokončit vysvětlení jednofotonových pokusů z rámečku 1. Už víme, že v interferenčním uspořádání (obrázek) je foton po průchodu interferometrem ve stavu |↑>, zatímco v bezinterferenčním uspořádání (obrázek) ve stavu i|→> – |↑> (nedošlo k poslední změně stavu na zrcadle P₂). Měření uskutečněné párem detektorů vlastně zjišťuje směr šíření fotonu: Stav fotonu |↑> vyvolá impulz v detektoru D₁, stav |→> impulz v D₂. Pro interferenční uspořádání je tedy výsledek jasný – foton ve stavu |↑> může být registrován jen detektorem D₁. V bezinterferenčním měření vznikne odezva na stav i|→> – |↑> buď v detektoru D₁, nebo v D₂, přičemž pravděpodobnosti obou těchto možností jsou stejné (tedy 50 %) v důsledku rovnosti absolutních hodnot obou koeficientů (i a –1) v superpozici.

Vraťme se k elektronu ve stavu |Ψ>=α|E₁> + β|E₂>. K jakým výsledkům by na něm vedla měření jiných veličin než energie, např. měření polohy? Kvadrát absolutní hodnoty vlnové funkce (viz rámeček 3 ), tj. |Ψ(r)|², určuje pravděpodobnost nalezení částice v místě r. Protože se vlnové funkce jednotlivých vzbuzených stavů velice liší (viz Obrázek ), závisí pravděpodobnostní rozdělení naměřené polohy na tom, jaké konkrétní dva energetické stavy do naší superpozice vstupují. Obecně, pro jakékoliv dvě veličiny A a B aparát kvantové mechaniky umožňuje danou superpozici Σ_aα_a|a>, odpovídající veličině A, přepsat jako superpozici Σ_bβ_b|b>, odpovídající veličině B. Tak jsou pravděpodobnosti výsledků měření B určeny i tehdy, byl-li stav zadán jako superpozice odpovídající A. [Symbolem |a> jsme označili stavy, na nichž měření veličiny A dá jednoznačně hodnotu a, a sčítání vyznačené symbolem Σ_a probíhá přes všechny možné měřitelné hodnoty a (α_a jsou odpovídající koeficienty); analogicky pro veličinu B.] Obecně platí, že samotný stav |a>, pro nějž je výsledek měření A jednoznačný, může být superpozicí více stavů |b>, takže výsledek měření B již jednoznačný být nemusí. To dokumentují i elektronové vlnové funkce vzbuzených stavů atomu vodíku na s.191: u stavů s určitou hodnotou energie se zde projevuje „rozmazání“ polohy.

Tu asi nejzvláštnější vlastnost kvantového měření jsme si nechali až na konec. Kvantové měření totiž mění stav měřeného systému. Podívejme se např., v jakém stavu se bude náš elektron nacházet po ukončení měření energie. Kdyby to byl původní stav α|Ε₁> + β|Ε₂>, mohlo by další měření energie na tomtéž elektronu vést k jiné hodnotě, než byla zjištěna v měření předchozím. To by v mnoha případech znamenalo rozpor s experimentální zkušeností ⁷⁾ . Pokud jednou byla naměřena hodnota např. E₁, další měření musí dát opět E₁ (zanedbáváme zde možný rušivý vliv okolí). Měření tedy musí měnit stav elektronu z uvažované superpozice |Ψ> do stavu, v němž je přítomna pouze jedna z přípustných alternativ: buď |Ε₁> (bylo-li naměřeno E₁), nebo |Ε₂> (bylo-li naopak naměřeno E₂).

Tomuto procesu redukce kvantových alternativ (stav α|Ε₁> + α|Ε₂> přechází buď na |Ε₁>, nebo na |E₂>) se říká kolaps vlnové funkce. Teprve jím se završuje proces kvantového měření. Přirozený časový vývoj stavu |Ψ> bez intervence měření je spojitý a jeho výsledek se dá z rovnic kvantové mechaniky předpovídat (vzpomeňte si na Schrödingera a jeho vlnovou funkci – spontánní kvantová evoluce je určena tzv. Schrödingerovou rovnicí). Naproti tomu kolaps vlnové funkce je skokový (okamžitý?) proces, jehož výsledkem je obecně náhodný (i když s naměřenou hodnotou jednoznačně související) stav. Odtud tedy pochází indeterministický charakter kvantové teorie. Právě tyto nezvyklé vlastnosti kvantového měření jsou dodnes zdrojem četných diskusí. /pokračování příště/

Poznámky

1) Kvantové stavy jsou reprezentovány vektory v n-rozměrném komplexním prostoru. Lineární kombinace (tedy superpozice) dvou či více vektorů je obecně nový vektor téhož prostoru.

2) Chápeme-li celou periodu jako 360°, pak čtvrt periody odpovídá 90°. Násobení imaginární jednotkou představuje pootočení v komplexní rovině právě o 90°.

3) V kvantové mechanice se obvykle používají tzv. normalizované stavy, což by v daném případě znamenalo, že |α|²+|α|²=1.

4) V důsledku interakcí může být stav kvantového systému „provázán“ se stavy okolí, a v takovém případě jej nelze popsat odděleně od „zbytku světa“, aniž bychom přitom o něm ztratili část informace. V čistém stavu se kvantový objekt nachází, když v daném okamžiku není provázán se svým okolím.

5) Dokonalá rozlišitelnost stavů |E₁gt a |E₂gt je v matematické formulaci kvantové mechaniky dána ortogonalitou („kolmostí“) odpovídajících stavových vektorů. Ta zaručuje, že např. pro elektron ve stavu |E₁gt nikdy nenaměříme energii E₂. V tomto článku uvažujeme výhradně superpozice vzájemně ortogonálních stavů.

6) V případě normalizovaného stavu je |α|²+|α|²=1, takže uvedené kvadráty jsou přímo rovny pravděpodobnostem.

7) Při měření polohy by např. nebyl důvod pro pozorování souvislých drah elementárních částic, jak je známe z dráhových detektorů.

)

Na obrázku A je schéma Machova-Zehnderova interferometru. Dopadající světelná vlna se na polopropustném zrcadle P₁ rozdělí na dvě vlny, které se šíří rameny interferometru a které se opět seběhnou na polopropustném zrcadle P₂. Budeme předpokládat, že interferometr má ramena stejně dlouhá a že vlna se při každém odrazu posune o čtvrtinu své periody. V takovém případě se ve směru detektoru D₁ vlny přicházející z obou ramen vzájemně posílí dojde ke konstruktivní interferenci. Naopak ve směru detektoru D₂ budou obě vlny v protifázi a vzájemně se vyruší dojde k destruktivní interferenci. Detektor D₂ nebude registrovat žádné světlo. Tak to funguje, přestože se světlo skládá z fotonů. I když bude v interferometru pouze jediný foton, detektor D₂ zůstane vždy němý. Aby foton mohl interferovat sám se sebou, musí být zároveň přítomen v obou ramenech interferometru. Jestliže ale provedeme měření bez polopropustného zrcadla P₂ viz obrázek B zjistíme, že foton přichází náhodně (se stejnými pravděpodobnostmi) buď jen z ramene I, nebo jen z ramene II.

Aritmetika Komplexních čísel

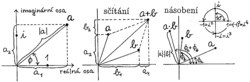Komplexní číslo, na rozdíl od čísla reálného, nelze znázornit na přímce, číselné ose, ale obecně si jej lze představit jako bod tzv. komplexní roviny (viz obrázek). Reálná číselná osa je v této rovině obsažena, bývá ztotožněna s vodorovnou osou, zatímco svislá osa se nazývá imaginární. Každé komplexní číslo a je kromě absolutní hodnoty |a|, což je jeho vzdálenost od bodu 0 (počátku souřadnic), charakterizováno také fází φ, tj. úhlem, který spojnice bodu 0 s bodem a svírá s vodorovnou osou. Tak pro kladná reálná čísla máme φ=0°, pro záporná φ=180°, pro čísla na imaginární ose φ=90° nebo φ=270° atd. Jak vidíme na obrázcích, komplexní čísla se dají sčítat i násobit, a vůbec se s nimi dá dělat všechno, co s čísly reálnými. Všimněme si bodu i na imaginární ose. Číslo reprezentované tímto bodem se nazývá imaginární jednotka (|i|=1) a spolu s obyčejnou reálnou jednotkou dostačuje k vyjádření libovolného komplexního čísla: a=a₁.1+a₂.i. Zde hodnoty a₁, resp. a₂ (souřadnice bodu a odečtené na reálné, resp. imaginární ose) tvoří reálnou, resp. imaginární část komplexního čísla a. Při sčítání komplexních čísel platí, že reálná část součtu je součtem reálných částí obou sčítanců, a podobně pro imaginární část. Při násobení se násobí absolutní hodnoty obou činitelů, zatímco fáze se sčítají. Z toho např. plyne vztah i²=i.i= 1 [neboli i=√(1)], který brzy využijeme při řešení našeho problému.

Vlnová funkce

Superpozice různých polohových stavů |r> částice (viz s. 190) je stavem, v němž přesná lokalizace částice v prostoru není možná. Můžeme si představit, že do superpozice |Ψ> vstupuje velký počet stavů |r>, každý s koeficientem α_r, tedy |Ψ> = Σ_rα_r|r> (symbol Σ_r znamená sčítání zahrnující všechny možné polohy r). Každému místu v prostoru je tak přiřazeno komplexní číslo α_r. Jinými slovy, koeficienty α_r tvoří komplexní funkci proměnné r. Právě tímto způsobem je definována vlnová funkce Ψ(r). Částice je současně přítomna ve všech místech, kde je její vlnová funkce různá od nuly. Existuje míra určující, jak ráda se částice popsaná funkcí Ψ(r) v tom kterém místě vyskytuje. Tato míra je dána kvadrátem absolutní hodnoty vlnové funkce, tj. hodnotou |Ψ(r)|².

Obliba některých míst prostoru a naopak nepřízeň vůči místům jiným je pro částice v různých kvantových stavech charakteristickou vlastností. Obrázky vlevo znázorňují průběh kvadrátu absolutní hodnoty vlnové funkce elektronu ve dvou vzbuzených stavech vodíkového atomu. Maxima odpovídají místům nejčastějšího výskytu elektronu třeba v rovině yz, tj. v místech r=(0,r_y,r_z), přičemž počátek souřadné soustavy splývá s polohou vodíkového jádra (protonu). Elektron vázaný v atomu vodíku, ať už je v libovolném vzbuzeném stavu, nemůže z dosahu silového působení jádra uniknout, a proto jeho vlnová funkce od jisté hranice rychle ubývá se zvyšující se vzdáleností od počátku. 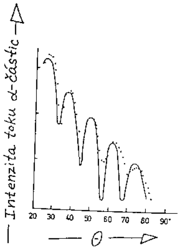Naopak při kolizích dvou částic např. v urychlovači nemusí k vytvoření vázaného stavu dojít a vzájemná interakce výrazně ovlivní tvar vlnové funkce rozptylující se částice i na velkých vzdálenostech od rozptylového centra. Na obrázku vpravo vidíte úhlovou závislost intenzity toku částic α (jader helia) o kinetické energii 40 megaelektronvoltů (tj. asi 6×10¹² joulů) pružně rozptýlených atomovými jádry titanu (úhel θ představuje odchylku částic α od původního směru šíření). Maxima a minima této závislosti jsou důsledkem interference.

Měření polarizace fotonu

Dopadá-li svazek obyčejného světla na vhodně vybroušený krystal islandského vápence, dělí se na svazky dva, tzv. řádný a mimořádný, které jsou lineárně, vůči sobě kolmo polarizovány. Lineární polarizace světla spočívá v tom, že vektor elektrického pole kmitá pouze v jednom směru (kolmém ke směru šíření vlny). Kvantové vysvětlení polarizace souvisí s vlastním momentem hybnosti (spinem) fotonu. Lineární polarizaci fotonu ve směru x (viz obrázek) odpovídá kvantový stav, který označíme |x> (přesněji řečeno, mluvíme zde pouze o polarizační části stavu fotonu); polarizaci ve směru y přísluší stav |y>. Stav lineární polarizace |x> v libovolném jiném směru x se dá vyjádřit jako superpozice stavů |x> a |y>: Je-li θ úhel sevřený osami x a x, pak platí, že |x>=cosθ|x>+sinθ|y>. Světlo však může mít také kruhovou či eliptickou polarizaci, odpovídající světelné vlně s vektorem elektrického pole rotujícím po kružnici či elipse. Superpozice stavů |x> a |y> s obecnými komplexními koeficienty odpovídají všem těmto možným polarizačním stavům.

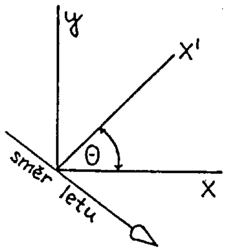Dopadá-li světelný svazek lineárně polarizovaný ve směru x odpovídajícím úhlu θ=45° na krystal s polarizačními směry x a y, je světelná intenzita každého z vystupujících polarizovaných svazků rovna polovině intenzity původní. Co se však stane, dopadá-li na krystal pouze jediný foton v polarizačním stavu |x>? Vzhledem k tomu, že foton je nedělitelný, můžeme jej zaregistrovat vždy buď jen ve směru šíření řádného svazku (řekněme s polarizací x), nebo ve směru šíření mimořádného svazku (s polarizací y). Zjištění, že foton jde cestou řádného svazku, tedy znamená naměření polarizace ve směru x a podobně nalezení fotonu v mimořádném svazku odpovídá naměření polarizace ve směru y. Oba tyto výsledky mají v našem speciálním případě pravděpodobnost 50 %, protože |cos 45°|²=|sin 45°|²=1/2. Víme-li, že se foton dal cestou řádného (resp. mimořádného) svazku, víme také, že je určitě ve stavu |x> (resp. |y>) jeho stav se tedy změnil. Výsledek následného měření polarizace v jakýchkoliv jiných směrech než x a y (včetně měření v původním směru x) bude neurčitý.