Kvantové hlavolamy V.
Albert Einstein se domníval, že kvantový popis fyzikálních systémů je neúplný, že by mělo být možno obejít se bez principiální neurčitosti (náhodnosti) a bez dalších bizarních vlastností kvantové teorie. Laboratorní testy založené na teoretických pracích Johna Bella ale naznačují, že se pravděpodobně mýlil.
Dva odlišné pohledy na kvantovou mechaniku
V Kvantových hlavolamech IV. (Vesmír 77, 333, 1998/6) jsme se stručně seznámili se dvěma různými filozofickými přístupy ke kvantové teorii. Podle Einsteinova názoru by měly prvky fyzikální teorie vystihovat skutečné, nezávisle na teorii existující vlastnosti systému. Teorie by navíc měla být deterministická (s možností přesné predikce vývoje systému a výsledků měření) a lokální (bez okamžitého působení na dálku). Z této pozice se kvantová mechanika jeví jako neúplná teorie: Její statistický charakter je důsledkem neznalosti nějakých „skrytých“ parametrů, které nekontrolovaně nabývají nejrůznějších hodnot, ale jejichž dynamika by měla být popsatelná nějakou „hlubší“ teorií, vyhovující uvedeným představám. Podle Bohrova názoru je třeba fyzikální teorii chápat spíše jen jako soubor vztahů mezi měřitelnými veličinami a připustit navíc, že náhoda může být neodstranitelnou součástí fyzikálního světa. Bohr říká, že pojmy jako poloha či hybnost částice nemusí mít v kvantovém světě smysl samy o sobě; fyzika se zabývá tím, co nám ukazují měřicí přístroje.Ukázali jsme, jak se A. Einstein, B. Podolsky a N. Rosen (EPR) snažili pomocí myšlenkové konstrukce využívající propleteného páru částic (na základě předpokladů lokality a reality) nalézt spor s principem neurčitosti. Tím chtěli dokázat, že kvantová mechanika není úplnou teorií. Podle principu neurčitosti nelze nikdy jednoznačně předpovědět výsledky měření polarizace zároveň v soustavě xy a x’y’ podle obrázku v rámečku 1 (např. je-li foton ve stavu x, je výsledek měření polarizace v soustavě x’y’ zcela neurčitý). Podle EPR by naopak měly existovat elementy reality odpovídající všem možným polarizacím. Tedy již v okamžiku zrození fotonu by mělo být nějak určeno, jak dopadnou všechna myslitelná polarizační měření.
V tomto pokračování si ukážeme, jak lze dávný spor mezi Einsteinem a Bohrem rozsoudit experimentálně. V roce 1964 odvodil John Bell nerovnosti mezi měřitelnými veličinami, které musí splňovat každá teorie se „skrytými“ parametry vyhovující kritériu lokality, avšak kvantová mechanika je obecně porušuje.
Bellovy nerovnosti
Představme si, že kvantová mechanika je skutečně neúplná teorie a že opravdu existují elementy reality určující výsledky měření polarizace fotonu ve všech různých směrech. V takovém případě by mělo být možné vybudovat teorii se „skrytými“ parametry, která by vyhovovala všem předpokladům požadovaným zastánci EPR.Uvažujme měření polarizace na obou fotonech z „propleteného“ páru (viz rámeček 1 ) pro nějaké dva úhly θ1 a θ2 natočení polarizačních hranolů v obou ramenech vůči nějaké pevné „laboratorní“ soustavě souřadnic. Výsledek polarizačního měření na prvním fotonu si označme jako A(θ1), přičemž A(θ1) = +1 v případě, že foton je polarizován ve směru určeném úhlem θ1, a A(θ1) = –1 pokud není (tedy pokud je polarizován ve směru kolmém). Podobně zavedeme proměnnou B(θ2), které přisoudíme hodnotu +1 nebo –1 podle toho, jestli nalezneme druhý foton polarizovaný ve směru určeném úhlem θ2, nebo ve směru kolmém. 1) Před měřením samozřejmě nevíme, jaké výsledky dostaneme. Podle zastánců teorií se skrytými parametry jsou však hodnoty A(θ1) a B(θ2) předem dány (jsou určeny v okamžiku emise fotonového páru, a to dokonce pro všechny možné úhly) a závisí na hodnotě nějakého skrytého parametru (nebo na několika takových parametrech). Hodnota skrytého parametru může být pro každý emitovaný pár jiná, takže náhodnost výsledků měření je důsledkem náhodnosti skrytého parametru.
Vždy když se snažíme najít řád v něčem, co se chová náhodně, musíme být trpěliví a provést velké množství pozorování, abychom byli schopni postřehnout nějaké trendy, zjistit např., které hodnoty se objevují nejčastěji, jak moc se odchylují od nějaké střední hodnoty apod. Střední hodnota je důležitým ukazatelem a budeme ji potřebovat i v dalším výkladu. Je to „průměr“ přes všechny možné hodnoty, kterých může veličina v principu nabývat, s ohledem na to, že některé se mohou vyskytovat pravděpodobněji než jiné. Odhad střední hodnoty z experimentálních dat provedeme tak, že sečteme všechny výsledky získané v jednotlivých opakováních experimentu a součet vydělíme počtem provedených opakování pokusu (tj. celkovým počtem naměřených hodnot). Čím více opakování, tím přesnější bude odhad střední hodnoty. Střední hodnotu budeme značit úhlovými závorkami .
Abychom se ale dostali k Bellovým nerovnostem: Řekněme, že máme čtyři proměnné α, θ, α’, β’, které mohou nabývat hodnot plus nebo minus jedna. Sestavme z nich následující výraz:
γ = αβ + αβ’ + α’β – α’β’.
Za každé řecké písmenko na pravé straně můžeme dosadit +1 nebo –1 a spočítat hodnotu γ. Co dostaneme, ukazuje následující tabulka (viz obrázek):
Funkce γ tedy nabývá pouze hodnot +2 nebo –2. Je zřejmé, že když zprůměrujeme jakýkoli počet hodnot γ spočtených pro libovolně vybraná α, β, α’, β’, výsledek nemůže být nikdy menší než –2 ani větší než +2. Obecněji, ať už jsou pravděpodobnosti výskytu γ= +2 a γ= –2 jakékoli, střední hodnota bude vždy ležet mezi –2 a +2:
–2≤<γ>≤+2.
Už asi tušíte, že za α můžeme dosadit naše A(θ1) a za γ zase B(θ2); za α’ a β’ pak hodnoty A(θ’1) a B(θ’2) pro nějaké obecně odlišné úhly θ’1 a θ’2 natočení polarizačních hranolů:
α=A(θ1), β=B(θ2), α’=A(θ1’), β’=B(θ2’).
Protože střední hodnota součtu je rovna součtu středních hodnot, lze výše odvozený výraz pro <γ> zapsat ve tvaru
–2 ≤ <αβ> + <αβ’> + <α’β> – <α’β’> ≤ +2.
A to jsou právě slavné Bellovy nerovnosti. (Proměnné teď značí výsledky polarizačních měření na obou fotonech pod zvolenými úhly; střední hodnota <αβ> = <A(θ1)B(θ2)> atd.) Pokud se chování párů fotonů řídí libovolnou lokální teorií se skrytými parametry, musí být tyto nerovnosti splněny (pro libovolné kombinace úhlů).
A co na to kvantová mechanika? Ta umožňuje střední hodnoty typu <A(θ1)B(θ2)> přímo vypočítat. Zvláště náročné čtenáře odkazujeme na odvození v rámečku 2 . Ostatní nám musí věřit, že výsledek závisí pro daný kvantový stav |x>1|y>2 – |y>1|x>2 na rozdílu úhlů natočení prvního a druhého polarizačního hranolu podle grafu na obrázku.
 Teď už není těžké ukázat, že kvantová mechanika výše uvedené Bellovy nerovnosti obecně porušuje! Vyberme dva úhly natočení prvního polarizačního hranolu θ1= 0°, θ1’= 45° a dva úhly natočení druhého hranolu θ2=112,5°, θ2’= 67,5° (viz obrázek) a uvažujme měření se všemi kombinacemi těchto úhlů. Když si dáte práci s odečtením několika hodnot na obrázku, zjistíte, že podle kvantové mechaniky pro takto zvolené úhly musí platit:
Teď už není těžké ukázat, že kvantová mechanika výše uvedené Bellovy nerovnosti obecně porušuje! Vyberme dva úhly natočení prvního polarizačního hranolu θ1= 0°, θ1’= 45° a dva úhly natočení druhého hranolu θ2=112,5°, θ2’= 67,5° (viz obrázek) a uvažujme měření se všemi kombinacemi těchto úhlů. Když si dáte práci s odečtením několika hodnot na obrázku, zjistíte, že podle kvantové mechaniky pro takto zvolené úhly musí platit:
<αβ> + <αβ’> + <α’β> – <α’β’> = –cos(225°) – cos(135°) – cos(135°) + cos(45°) = 2√2.
To je dokonce větší než 2,8, tím spíš tedy větší než 2!
Tento výsledek je pro fyziku velice důležitý. Jednak ukazuje, že kvantovou teorii nelze nahradit žádnou „klasickou“ teorií splňující EPR kritéria popsaná v minulé části (Vesmír 77, 333, 1998/6), jednak nabízí možnost (a to je skoro důležitější), jak mezi kvantovou mechanikou a teoriemi se skrytými parametry rozhodnout experimentálně. O několika takových experimentech se zmíníme v příští kapitole. Ale nebudeme vás napínat: všechny docela přesvědčivě hovoří ve prospěch kvantové mechaniky.
Experimentální testy Bellových nerovností
První experimentální testy Bellových nerovností provedli Stuart J. Freedman a John F. Clauser v Berkeley r. 1972. Využívaly se v nich fotony s korelovanými polarizacemi, vyzářené při kaskádních přechodech elektronů mezi určitými energetickými hladinami v atomu vápníku.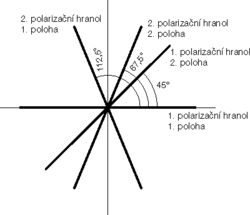 Postupně se objevovaly další experimenty, patří mezi ně např. práce Edwarda S. Frye a Randalla C. Thompsona z Texasu (1975), Alaina Aspecta, Jeana Dalibarda a Gérarda Rogera v Orsay (1976–1983), Z. Y. Oua a Leonarda Mandela v Rochesteru (1988) a mnoha dalších. Již nejranější práce převážně potvrzovaly předpovědi kvantové mechaniky, nicméně jejich výsledky nebyly dostatečně průkazné. Postupně se ovšem experimenty zdokonalovaly a jejich přesnost zvyšovala.
Postupně se objevovaly další experimenty, patří mezi ně např. práce Edwarda S. Frye a Randalla C. Thompsona z Texasu (1975), Alaina Aspecta, Jeana Dalibarda a Gérarda Rogera v Orsay (1976–1983), Z. Y. Oua a Leonarda Mandela v Rochesteru (1988) a mnoha dalších. Již nejranější práce převážně potvrzovaly předpovědi kvantové mechaniky, nicméně jejich výsledky nebyly dostatečně průkazné. Postupně se ovšem experimenty zdokonalovaly a jejich přesnost zvyšovala.
Zastavme se teď stručně u experimentů Aspectovy skupiny ve Francii, 2) které se považují za první opravdu věrohodné testy Bellových nerovností. Jako zdroj fotonových párů byl využíván svazek vápníkových atomů, které byly pomocí dvou laserů vybuzeny do stavů s vyšší energií. Atomy v těchto stavech dlouho nevydrží a vyzářením fotonu (o vlnové délce 551,3 nanometru) přecházejí do stavu s nižší energií a odtud téměř okamžitě do původního stabilního stavu (s nejnižší energií), přičemž vyzáří druhý foton (o vlnové délce 422,7 nm). Protože původní i excitovaný stav atomu vápníku mají oba nulový moment hybnosti, zatímco „mezistav“ má nenulový moment hybnosti, klade zákon zachování celkového momentu hybnosti určitá omezení i na polarizace obou vyzářených fotonů – vzniká pár fotonů v propleteném stavu s korelovanými polarizacemi. 3)
 Schéma experimentu je na obrázku. Pro zjišťování polarizace fotonů byly využity tzv. Wollastonovy hranoly, sestavené ze dvou kusů speciálně vybroušených krystalů islandského vápence (foton se ve Wollastonově hranolu musí „rozhodnout“ pro jednu ze dvou cest odpovídajících dvěma určitým vzájemně kolmým lineárním polarizacím). Při odvození Bellových nerovností se předpokládá, že nastavení orientace polarizačního hranolu v jednom rameni neovlivní měření ve druhém rameni (nebo dokonce proces přípravy páru) klasickou cestou – tj. prostřednictvím nějaké interakce šířící se mezi oběma polarizačními hranoly (a zdrojem fotonů). Aby se tato možnost skutečně vyloučila, byl experiment uspořádán tak, že k nastavení úhlů polarizačních hranolů docházelo vždy až po emisi páru, takže žádný klasický signál (pohybující se nanejvýš rychlostí světla) nestíhal přenést informaci o nastavení jednoho polarizačního hranolu ke druhému před okamžikem měření. Prakticky se to realizovalo pomocí tzv. akusticko-optických přepínačů, umístěných v každém rameni. Akusticko-optický přepínač umožňuje ve velmi krátké době změnit směr světelného paprsku. Každý z těchto přepínačů směroval přicházející foton vždy na jeden či druhý ze dvou různě nastavených polarizačních hranolů v každém rameni (viz obrázek). Oba přepínače byly ovládány nezávislými oscilátory (jedním pro každé rameno) s průměrnou periodou přepínání kolem 10 nanosekund. Vzdálenost přepínačů a polarizačních hranolů od zdroje byla zhruba 6 m, což odpovídá době šíření fotonu asi 20 ns (světelný signál od jednoho polarizačního hranolu ke druhému by letěl 40 ns). To znamená, že než oba fotony dospěly k přepínačům, mohl se již (ale nemusel) stav přepínačů změnit.
Schéma experimentu je na obrázku. Pro zjišťování polarizace fotonů byly využity tzv. Wollastonovy hranoly, sestavené ze dvou kusů speciálně vybroušených krystalů islandského vápence (foton se ve Wollastonově hranolu musí „rozhodnout“ pro jednu ze dvou cest odpovídajících dvěma určitým vzájemně kolmým lineárním polarizacím). Při odvození Bellových nerovností se předpokládá, že nastavení orientace polarizačního hranolu v jednom rameni neovlivní měření ve druhém rameni (nebo dokonce proces přípravy páru) klasickou cestou – tj. prostřednictvím nějaké interakce šířící se mezi oběma polarizačními hranoly (a zdrojem fotonů). Aby se tato možnost skutečně vyloučila, byl experiment uspořádán tak, že k nastavení úhlů polarizačních hranolů docházelo vždy až po emisi páru, takže žádný klasický signál (pohybující se nanejvýš rychlostí světla) nestíhal přenést informaci o nastavení jednoho polarizačního hranolu ke druhému před okamžikem měření. Prakticky se to realizovalo pomocí tzv. akusticko-optických přepínačů, umístěných v každém rameni. Akusticko-optický přepínač umožňuje ve velmi krátké době změnit směr světelného paprsku. Každý z těchto přepínačů směroval přicházející foton vždy na jeden či druhý ze dvou různě nastavených polarizačních hranolů v každém rameni (viz obrázek). Oba přepínače byly ovládány nezávislými oscilátory (jedním pro každé rameno) s průměrnou periodou přepínání kolem 10 nanosekund. Vzdálenost přepínačů a polarizačních hranolů od zdroje byla zhruba 6 m, což odpovídá době šíření fotonu asi 20 ns (světelný signál od jednoho polarizačního hranolu ke druhému by letěl 40 ns). To znamená, že než oba fotony dospěly k přepínačům, mohl se již (ale nemusel) stav přepínačů změnit.
Výsledky experimentu se v rámci přesnosti měření shodovaly s předpovědí kvantové mechaniky a spolehlivě prokázaly narušení Bellových nerovností.
Do dnešního dne byla provedena řada dalších podobných experimentů. Optická vláknová technologie umožnila testovat narušení Bellových nerovností až na vzdálenosti desítek kilometrů. (To má kromě psychologického účinku – tak „dlouhého“ dosahu je kvantová nelokalita – také technický význam pro omezení možnosti vzájemného klasického ovlivnění přístrojů.) Také se objevily nové zdroje propletených fotonových párů. Výsledky provedených experimentů jsou v dobré shodě s kvantovou mechanikou. Mimochodem, nelokální kvantová korelace nalézá uplatnění i v kvantové kryptografii – v metodě bezpečné komunikace založené právě na „zvláštnostech“ kvantových zákonů. 4)
Vášeň na dálku
I když lze v dosud provedených experimentech ještě nalézt nepatrné skulinky, 5) vše nasvědčuje tomu, že pravdu má kvantová mechanika se všemi svými podivnostmi. Musíme se smířit s tím, že kvantový stav představuje úplný popis reality a že neurčitost s tím spojená je objektivní; není důsledkem naší neznalosti a nelze se jí nijak vyhnout. 6)Polarizace fotonů tvořících propletený pár nejsou předem určeny. Provedeme-li měření na jednom fotonu, druhý foton se „dozví“ o jeho výsledku bez ohledu na to, jak je daleko! Dojde totiž ke kolapsu vlnové funkce celého systému, tedy obou fotonů. Vlnová funkce se v důsledku měření změní naráz v celém prostoru. V tomto smyslu je kvantová mechanika opravdu nelokální – porušuje předpoklad lokality (Vesmír 77, 335, 1998/6). Přitom se ale zdá, že nic „opravdového“ se okamžitě v celém prostoru nemění. Nic reálně měřitelného (jako například energie) se při kolapsu vlnové funkce fotonového páru na dálku nepřenáší. Kvantová nelokalita neporušuje kauzalitu, což znamená, že ji nelze použít např. na posílání zpráv nadsvětelnou (nebo dokonce nekonečnou) rychlostí. Výsledky měření polarizace na obou fotonech jsou sice korelované (výsledek prvního měření „ovlivní“ výsledek druhého), nicméně konkrétní změřené hodnoty jsou zcela náhodné. Pozorovatelé provádějící měření na obou fotonech tuto korelaci mohou odhalit teprve tehdy, když svoje výsledky vzájemně porovnají. 7) Je to jen taková neškodná „vášeň na dálku“.
 Jestli si moc nedovedete představit, co to všechno vlastně znamená, přečtěte si ještě následující příměr, který volně přebíráme od Johna Bella: 8) Vyklíčilo podezření, že sledování televize způsobuje pokles porodnosti (viz obrázek). Není však zcela jasné, který ze dvou hlavních programů (ČT1 či TV Nova) je více vinen. Světlo do problému by mohlo vnést následující statistické šetření: Ve dvou městech, např. v Praze a Olomouci, by byl vysílán vždy pouze jeden z obou televizních programů. O tom, který program to v daný den bude, by každé ráno rozhodli například radní příslušného města – třeba hodem mincí. Volba by tedy byla v obou městech provedena každý den zcela nezávisle. Průběžně by se sledovaly počty početí v jednotlivých dnech. Těžko říci, k jakému verdiktu by se ohledně inkriminovaných televizních programů dospělo. Zajímavější pro nás je otázka, zda by počty početí v Praze a v Olomouci byly statisticky nezávislé (nekorelované). Na první pohled se zdá, že by nezávislé být měly, věc je ale trochu složitější. Pravděpodobnost početí totiž kromě televizních programů ovlivňují jistě také nejrůznější faktory společné pro obě města, např. počasí, obchody na burze apod., a ty určitou korelaci způsobovat mohou (když je hezký večer, lidé se tolik nekoukají na televizi, ale jdou třeba do parku a jsou uchváceni krásou stromů, pomníků a zaujati sebou navzájem; to se jistě děje v obou městech). Pokud by vzájemná korelace plození potomstva v obou městech souvisela jen s těmito „skrytými parametry“, bylo by možné pro každodenní počty početí v jednotlivých městech při různých kombinacích televizních programů odvodit nerovnosti analogické nerovnostem Bellovým. Důsledky porušení Bellových nerovností popsané v tomto článku lze přirovnat k tomu, že by se korelace četností početí v obou městech nedaly vysvětlit pouze počasím ani jinými „skrytými parametry“, ale jen tím, že pravděpodobnost početí v Praze závisí vedle televizního programu vysílaného v Praze (a vedle mnoha dalších faktorů) také na programu vysílaném v Olomouci a naopak. 9) Jestli tomu stále ještě nerozumíte (nebo už zase nerozumíte), nebuďte smutní. Kvantová mechanika je prostě taková – trochu tajemná. Přečtěte si raději na závěr slova Richarda Feynmana:
Jestli si moc nedovedete představit, co to všechno vlastně znamená, přečtěte si ještě následující příměr, který volně přebíráme od Johna Bella: 8) Vyklíčilo podezření, že sledování televize způsobuje pokles porodnosti (viz obrázek). Není však zcela jasné, který ze dvou hlavních programů (ČT1 či TV Nova) je více vinen. Světlo do problému by mohlo vnést následující statistické šetření: Ve dvou městech, např. v Praze a Olomouci, by byl vysílán vždy pouze jeden z obou televizních programů. O tom, který program to v daný den bude, by každé ráno rozhodli například radní příslušného města – třeba hodem mincí. Volba by tedy byla v obou městech provedena každý den zcela nezávisle. Průběžně by se sledovaly počty početí v jednotlivých dnech. Těžko říci, k jakému verdiktu by se ohledně inkriminovaných televizních programů dospělo. Zajímavější pro nás je otázka, zda by počty početí v Praze a v Olomouci byly statisticky nezávislé (nekorelované). Na první pohled se zdá, že by nezávislé být měly, věc je ale trochu složitější. Pravděpodobnost početí totiž kromě televizních programů ovlivňují jistě také nejrůznější faktory společné pro obě města, např. počasí, obchody na burze apod., a ty určitou korelaci způsobovat mohou (když je hezký večer, lidé se tolik nekoukají na televizi, ale jdou třeba do parku a jsou uchváceni krásou stromů, pomníků a zaujati sebou navzájem; to se jistě děje v obou městech). Pokud by vzájemná korelace plození potomstva v obou městech souvisela jen s těmito „skrytými parametry“, bylo by možné pro každodenní počty početí v jednotlivých městech při různých kombinacích televizních programů odvodit nerovnosti analogické nerovnostem Bellovým. Důsledky porušení Bellových nerovností popsané v tomto článku lze přirovnat k tomu, že by se korelace četností početí v obou městech nedaly vysvětlit pouze počasím ani jinými „skrytými parametry“, ale jen tím, že pravděpodobnost početí v Praze závisí vedle televizního programu vysílaného v Praze (a vedle mnoha dalších faktorů) také na programu vysílaném v Olomouci a naopak. 9) Jestli tomu stále ještě nerozumíte (nebo už zase nerozumíte), nebuďte smutní. Kvantová mechanika je prostě taková – trochu tajemná. Přečtěte si raději na závěr slova Richarda Feynmana:
Byly časy, kdy noviny psaly, že pouze dvanáct lidí rozumí teorii relativity. Nevěřím, že tomu tak kdy bylo. Možná bylo období, kdy jí rozuměl pouze jeden člověk, protože byl tím jediným, kdo ji měl v hlavě dřív, než napsal svůj článek. Ale potom si lidé článek přečetli a mnoho z nich teorii relativity tak či onak porozumělo, rozhodně jich bylo víc než dvanáct. Naproti tomu si myslím, že mohu bezpečně prohlásit, že není nikdo, kdo by rozuměl kvantové mechanice. 10) 11)
Poznámky
Propletený stav
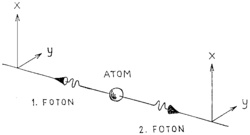 Ve čtvrté části Hlavolamů jsme popsali situaci, kdy atom vyzáří dva fotony do opačných směrů takovým způsobem, že nikdy nemohou být nalezeny oba se stejnou polarizací (viz obrázek). Kvantově můžeme stav takové dvojice fotonů popsat superpozicí, která má např. v referenční soustavě xy tvar |x>1|y>2
Ve čtvrté části Hlavolamů jsme popsali situaci, kdy atom vyzáří dva fotony do opačných směrů takovým způsobem, že nikdy nemohou být nalezeny oba se stejnou polarizací (viz obrázek). Kvantově můžeme stav takové dvojice fotonů popsat superpozicí, která má např. v referenční soustavě xy tvar |x>1|y>2
)> podle kvantové mechaniky
Zapíšeme si kvantový stav našich dvou korelovaných fotonů znovu, tentokrát v normovaném tvaru:
|Ψ> = 1/√2|x>1|y>2
Ke stažení
 Článek ve formátu PDF [127,41 kB]
Článek ve formátu PDF [127,41 kB]