Pouť za harmonií světa

Hudba stála u vzniku vědy a svým způsobem jí stále ukazuje cestu. Stála u pochopení vesmíru i objevu anestezie. „Hudba je s ničím neporovnatelná radost duše, která počítá, aniž to ví,“ řekl kdysi Wilhelm Gottfried Leibniz. Co vědu (a matematiku výslovně) s hudbou spojuje a co obě disciplíny dělí? Co jedna druhé může dát?

Jak už to u velkých objevů bývá – málokdy se dají udělat prostou extrapolací stávajícího poznání. Zvídavý Pythagoras, jeden z prvních filosofů v dějinách lidstva (mimo jiné pravděpodobný autor termínu filosofie), si opatřil monochord a na něm začal zkoumat, jak spolu souvisejí vlastnosti struny a jejího tónu (vnímaného smysly relativně prostřednictvím intervalů). To, na co tehdy přišel, pro něho muselo být doslova zjevení: nejenže výška tónu závisí na délce struny, ale vztah mezi těmito dvěma veličinami lze pro intervaly čistého ladění vyjádřit pomocí malých celých čísel a jejich zlomků (takže kupříkladu tón o oktávu vyšší vydává struna poloviční délky). Hudba, ta pomyslná mluva olympských bohů prostředkovaná lidským živáčkům Múzami z Parnasu, je vystavěna z čísel!

Pythagoras v Dějinách filosofie Thomase Stanleye.

Následně Pythagoras a jeho žáci pojali hudební akustiku za jakýsi ideální mustr pro veškeru přírodovědu a dospěli k závěru, že všechno bytí i dění v přírodě je popsatelné čísly a dá se vyjádřit pomocí jednoduchých matematických vztahů a operací, které jsou ve vzájemné harmonii (harmonie ve starořečtině znamená skloubení). Hezky to vystihl Aristoteles, který o Pythagorejcích napsal: „A tak nebe jejich, všechno je číslo a harmonie.“

Pythagorejci tudíž už před dvěma a půl tisíciletími – byť vysoce spekulativně – skrze hudbu vnesli do věd o přírodě matematiku a učinili je vědami exaktními. Věda v jejich (v podstatě dodnes platném) pojetí pak není nic jiného než hledání harmonie přírody vyjadřované matematickými prostředky.

Od mystéria k harmonii

Dlouho, až do počátku novověku (kdy přišel Mikuláš Koperník), lidé věřili, že Země je nehybným středem vesmíru, kolem kterého se všechno, co na obloze vidíme, stačí za jediný den otočit. Ale jak to, že se přitom celá ta složitá sestava nepomíchá? Pomohla představa, že hvězdné nebe je upevněno na povrchu jakési duté průhledné koule, takzvané sféry, která se otáčí kolem Země a „veze“ na sobě všechny ty tisíce hvězd. A jelikož některé „hvězdy“ na obloze mezi ostatními putují po své vlastní dráze, musela i každá planeta mít svoji vlastní sféru nacházející se uvnitř sféry stálic.

Okouzleni poznatky z hudební akustiky, aplikovali je Pythagorejci i na vesmír – velikosti a pohyby nebeských sfér nejsou podle nich nahodilé, nýbrž podle přísných matematických pravidel sladěné tak, že při svém věčném otáčení znějí dokonalým akordem, jedinečnou harmonií, kterou smrtelník může vnímat jen rozumem, nikoli sluchem. Onen pomyslný dokonalý souzvuk všehomíra nazývali hudba sfér nebo harmonie sfér.

Johannes Kepler sto let po Koperníkovi už na ladné povrzávání nebeského mechanismu nedal, ale jinak měl Pythagora hluboko zadřeného; spolu s ním věřil, že příroda funguje v prostých matematických poměrech obdobných těm v hudební harmonii. A také že existuje symetrie mezi pythagorovskou aritmetikou (čísly) a geometrií (útvary).

Keplerovo Kosmografické mystérium, 1596, schéma plenátárních drah.

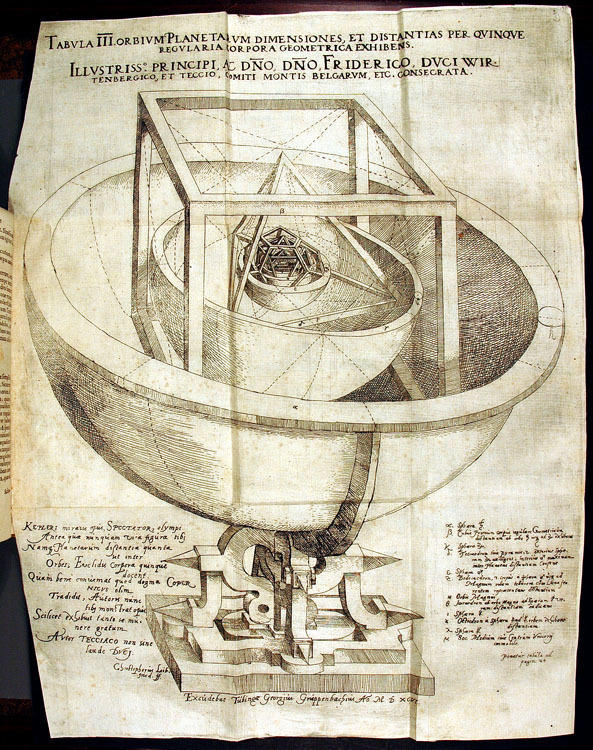
Kepler to napřed zkusil s geometrií. Jako mladý profesor gymnázia ve Štýrském Hradci přišel při kreslení na tabuli během výkladu o drahách dvou nejvzdálenějších tehdy známých planet Jupitera a Saturna na prazvláštní věc: do zhruba rovnostranného trojúhelníku vepsaného do dráhy Saturna se nečekaně přesně vešla oběžná dráha Jupitera! Líhnoucímu se astronomovi tahle náhoda nedala spát – co když jsou vzájemné velikosti planetárních drah vytvořeny právě tak, že mezi ně lze vložit takový pravidelný mnohoúhelník, aby byl současně opsaný dráze vnitřní planety a vepsaný dráze sousední planety vnější?

Okamžitě to začal zkoušet se všemi planetárními drahami a s nejrůznějšími možnými mnohoúhelníky, ale nešlo to. Jenže – vesmír je přece trojrozměrný, tak proč mu vnucovat rovinné útvary? Nebylo by lepší místo plochých drah použít jejich prostorovou představu (sféru) a místo pravidelných mnohoúhelníků pravidelná tělesa (tedy taková, jejichž stěnami jsou vždy jen stejné pravidelné mnohoúhelníky)? Těchto těles, kterým antičtí filosofové říkali dokonalá a připisovali jim magickou roli ve stavbě světa, je známo pět. A hle, právě tolik je mezer mezi sférami šesti (tehdy známých) planet! Nabuzený Kepler se pustil do práce a vskutku se mu podařilo každému planetárnímu mezisféří přiřadit jedno dokonalé těleso. Vznikla tato posloupnost sfér a těles: Merkur – osmistěn – Venuše – dvacetistěn – Země – dvanáctistěn – Mars – čtyřstěn – Jupiter – krychle – Saturn.

Objev „řádu vesmíru“ vyšel roku 1596 pod názvem Kosmografické mystérium a okamžitě svého autora proslavil. Měl jedinou, zato podstatnou vadu, kterou po několika letech odhalila Keplerova podrobnější pražská měření planetárních drah: Bylo to celé špatně, nefungovalo to.

Když tedy neuspěl s útvary, začal to zkoušet s čísly; zkoumal, jak se vztahy kolem hudebních intervalů uplatňují ve stavbě planetární soustavy. A nakonec formuloval třetí zákon oběhu planet, nazývaný též harmonický. Matematicky je až zázračně, chce se říci „hudebně akusticky“ jednoduchý: Poměr třetí mocniny velké poloosy eliptické oběžné dráhy planety ku druhé mocnině její oběžné doby je pro všechny planety stejný.

Přesvědčení, že teď už konečně kápl na tu pravou souhru sfér, vyjádřil i názvem své publikace – Harmonices Mundi (Harmonie světů). Vychází roku 1619 v Linci a sestává z pěti knih. První pojednává o pravidelných mnohoúhelnících, druhá o souměrnosti obrazů, třetí se zabývá původem harmonických poměrů v hudbě, čtvrtá rozebírá harmonické konfigurace v astrologii a pátá konečně obsahuje třetí zákon zasazený do úvah o harmonii pohybu planet. Kupříkladu skutečnost, že maximální úhlová rychlost Země mezi perihéliem a aféliem se mění v poměru 16:15, což odpovídá poměru délek strun znějících tóny E a F, komentuje Kepler slovy: „Země zpívá Mi, Fa, Mi.“

Takty a rovnice. Kapitola o matematice

Věnujme se nyní matematice. Od dob starých Pythagorejců tedy panuje přesvědčení, že královna věd má k hudbě blíž než jiné exaktní vědy. Keith Devlin, profesor matematiky na Stanfordu, v knize Jazyk matematiky (1976) píše: „Po takřka celou dobu 2500 let trvání západní civilizace, jejíž počátek spadá do období starověkého Řecka, se na matematiku a hudbu pohlíželo jako na dvě strany téže mince. Lidé věřili, že obě poskytují náhled na uspořádání vesmíru.“ Ale dodává: „Teprve s rozvojem vědeckých metod v 17. století se cesty matematiky a hudby rozdělily.“

A tak může Timothy Gowers, profesor matematiky z Cambridge, ve své knize Mathematics – a very short introduction (2002) suše konstatovat: „Drtivá většina matematiků je nemuzikálních. Nezájem o druhý obor vesměs platí i obráceně. Nepodařilo se prokázat, že by hudební výchova dětí nějak zlepšovala jejich matematické schopnosti.“

Takže – ano, matematika má k hudbě jistě blíž než jiné vědy, ale ne tolik, jak by si zřejmě mnozí přáli.

O harmonii tu už byla řeč. Rytmu se asi nejvíc týká nádherná sentence německého polyhistora Wilhelma Gottfrieda Leibnize, mj. vynikajícího matematika (a velký Johann Sebastian jako by ho slyšel): „Hudba je s ničím neporovnatelná radost duše, která počítá, aniž to ví.“

Rovněž instrumentace má svého advokáta; takto německý fyzik Ludwig Boltzmann horoval nad James Clerk Maxwellovým matematickým výkladem kinetické teorie plynů: „Nejprve se majestátně rozvíjejí variace rychlosti, pak z jedné strany vstupují rovnice stavu a z druhé rovnice pohybu ve středním poli; stále výš se vzdouvá zmatek vzorců; náhle slyšíme čtyři slova: ´dejme n = 5´. Zlý duch V (relativní rychlost dvou molekul, FH) zmizí a dominantní tón v basu náhle umlká; to, co se zdálo nepřemožitelným, je překonáno jako nějakým kouzelným proutkem. Není kdy říkat, proč byla zvolena ta nebo ona substituce; kdo to nevycítí, musí knihu odložit, neboť Maxwell nepíše programovou hudbu. Výsledek za výsledkem je podáván poddajnými vzorci, až nakonec jako neočekávané vyvrcholení přichází rovnováha tepla těžkého plynu; opona pak spadne.“

James Clerk Maxwell.

Public Domain

Tentýž učenec také opisuje matematický rukopis: „Jako hudebník pozná při prvních taktech Mozarta, Beethovena či Schuberta, tak rozezná matematik po několika stránkách svého Cauchyho, Gausse, Jacobiho nebo Helmholtze. Největší elegance charakterizuje Francouze, největší dramatická pádnost Angličany, především Maxwella.“

Umění, to jsem já; věda, to jsme my

Obecně řečeno, hudba i matematika sice obě operují se specificky formalizovanými abstraktními strukturami, ale výrazně jinak – zatímco matematik je víceméně veden k předem určenému (byť zprvu neznámému) cíli, komponista má ve své tvorbě mnohem větší míru volnosti – on si cíl i cestu k němu sám vybírá.

To je nejspíš hlavním důvodem, proč vztah mezi matematickými schopnostmi a hudebním nadáním, pokud vůbec, bývá spíš jednosměrný – matematici mohou rozumět hudbě, ale nedokážou ji skládat, zatímco pro muzikanty bývá matematika španělskou vesnicí.

Popsal to americký matematik polského původu Stanisław Ulam (jeden z hlavních konstruktérů americké vodíkové bomby): „Mám dobrou paměť na melodie a dovedu je poměrně přesně zapískat. Když se však snažím vymyslet nebo zkomponovat ´chytlavou´ melodii, zjišťuji s jistým pocitem bezmoci, že je to jen triviální kombinace melodií, které jsem už slyšel…“

Také cíle jsou odlišné – matematik hledá pravdu, kterou zachytí na papír a kterou pak ocení jen zasvěcenci z oboru, hudebník usiluje o co nejvyšší citový účin působící víceméně na každého (skladbu tedy nestačí složit a zapsat, ale musí se i provést). Dobrá matematika musí být logicky konzistentní (jedna chyba zničí vše), za dobrou hudbu považujeme takovou, která se nám „líbí“ (někomu víc, jinému míň).

Významný český matematik a varhaník Petr Hájek se nad vztahem hudby a matematiky zamyslel takto: „Co mají společného, je jakási abstraktnost. Myslím, že to byl Josef Bohuslav Foerster, kdo řekl, že skladatel je nejvíc podoben nebeskému tvůrci, poněvadž tvoří z ničeho. Hudba je skutečně abstraktní záležitost, není vidět, a v tom je podobná matematice. Rozdílná je zase tím, že v matematice jde o přesnou dedukci, v hudbě spíš o emoce, afekty. Rozhodně mají společný trochu jiný než běžný způsob existence. Těžko se o tom mluví – čím jsou pro mne matematika i hudba krásné, se mi jeví velmi podobné. Nicméně tak jako může matematický důkaz poskytnout estetický prožitek, tak lze naopak hudební dílo analyzovat jako jakousi přesnou strukturu, která má jisté zákonitosti matematicky popsatelné.“

Pominout však nelze ani další rozdíl. Dokonale ho vystihuje myšlenka rusko-belgického nobelovského chemika Ilyi Prigogina: „Bez Bacha bychom neměli Matoušovy pašije, zatímco teorie relativity by byla objevena i bez Einsteina.“

Obecněji to vyjádřil o sto let dříve francouzský fyziolog Claude Bernard: „Umění to jsem já, věda to jsme my.“

Další cesta vpřed musí mířit i dozadu

Vstup matematiky do věd o přírodě dal výzkumu hmotného světa křídla. Prakticky ale, jakkoli objem jednotlivých vědeckých poznatků lavinovitě narůstá, ona pomyslná hudba sfér nám stále uniká. Proč?

K tomu, abychom svět mohli popisovat matematikou, museli jsme ho zjednodušit, zredukovat jeho přirozenou složitost. A ve snaze najít ve svých výzkumech exaktní, co možná přesnou a úplnou odpověď jsme té matematiky stále přidávali. „Existuje podivuhodná možnost, že člověk dovede nějaký předmět ovládat matematicky, aniž by skutečně pochopil vtip celé věci… Hlavní věc je přece obsah, nikoli matematika,“ horlil Albert Einstein, když se před sto lety mořil s formulováním obecné teorie relativity.

Možná by nás, tak jako kdysi Pythagora, mohla opět inspirovat hudba. My se jí přece nekocháme tak, že si představujeme proměnlivé chvění vzduchu bušícího do ušního bubínku nebo že čteme party jednotlivých nástrojů, ale svěřujeme ji kompetentním muzikantům a potom „jenom“ posloucháme, co oni z těch partů vydolují. A stejně tak jako nechceme, aby hudba končila u svého notového zápisu, ale hrála se, poslouchala, obohacovala nás a uváděla do vytržení, ani věda nemůže skončit u zápisu matematického.

Představme si vzdělaného, zkušeného, ale i náležitě múzického vědce (nebo v opačném gardu vybaveného umělce) schopného hlubokého vhledu hraničícího s intuicí a svěřme mu všechny ty rozmanité vědecké „notové zápisy“. Nechejme ho, aby nám svět opět reprodukoval jako nekonečně veliký a složitý, přesto až magicky souladný živoucí celek, skrze nějž se tu a tam alespoň letmo dotkneme hudby sfér! I za cenu určité ztráty úplnosti a přesnosti, hlavně že – jak si přál Einstein – zůstane zachován onen „vtip celé věci“…

Možná bychom pak do vědy vedle pokračujícího redukování reality a další matematizace získaného reduktátu mohli vrátit panoramatický pohled, místo kvantity (za kterou jsme dlouho byli tak vděčni) se obrátili zpět ke kvalitě, od čísel ke slovům, a z pyramidy naměřených a vypočtených dat znovu složili co možná adekvátní obraz světa (kterému už bychom na rozdíl třeba od Keplera víc rozuměli).

Vědecké poznatky nechť v nás rezonují v co možná nejplnější harmonii, vždyť jen tak dokážeme ze zákonů přírody vyvodit co nejsprávnější základní zákony lidské.

Výzkumy a objevy s účastí hudby

Nelze zde nepřipomenout také objevy, jimž na svět pomohla hudba.

Když Galileo před čtyřmi sty lety studoval zákonitosti pohybu těles, měřil mimo jiné rychlost pohybu koule na proměnlivě naklonitelné rovině. Jelikož ještě neměl vhodnou časomíru, vodicí drážku roviny překřížil osmi strunami laděnými například do oktávy či do nápěvu nějaké jednoduché písničky. Když dosáhl maximální pravidelnosti brnknutí, změřil vzdálenost mezi strunami. Zjistil, že vzdálenosti strun se v průběhu dráhy neustále zvětšují. Rychlost roste pravidelně s časem, koule se pohybuje rovnoměrně zrychleně.

Leopold Auenbrugger jako syn hospodského už v mládí prakticky poznal, že plný a prázdný sud znějí při poklepání jinak. Jako vystudovaný doktor pak po letech výzkumů (i na mrtvolách, jejichž dutiny po vzoru sudů všelijak a všeličím zaplňoval) vydal roku 1761 spis, ve kterém popisuje „nový způsob, jak poklepáváním na hrudníku člověka možno v něm objevit skryté choroby“. Nová fyzikální vyšetřovací metoda poklepem by ale nevznikla bez autorova vynikajícího hudebního sluchu (napsal kupříkladu libreto k jedné z oper Mozartova současníka Antonia Salieriho).

O čtvrt století později neméně vytříbený hudební sluch pomohl René Laennecovi vynalézt další významnou fyzikální vyšetřovací metodu – poslech – i její pomůcku – stetoskop.

Španělský zpěvák a učitel zpěvu Manuel García byl tak zvědavý, jak vypadá jeho „hudební nástroj“, že se rozhodl „zviditelnit“ ho stůj co stůj. Použil k tomu zakoupený nový typ zubního zrcátka s dlouhým držadlem, které si (předem ohřáté v teplé vodě, neboť měl instrument svého živobytí taky rád) před zrcadlem vsunul do úst a položil na čípek měkkého patra. Druhým zrcátkem (obyčejným kapesním, které vzal sestře z kabelky) si do krku vrhl osvětlovací prasátko. V září 1854 tak své hlasivky jako první na světě skutečně uviděl a stal se vynálezcem laryngoskopu neboli krčního zrcátka.

Dva roky se Dmitrij Ivanovič Mendělejev, mimo jiné hlava muzikální rodiny, ve dne v noci trudil nad problémem, jak smysluplně uspořádat soubor známých chemických prvků. Jednoho raně březnového dne roku 1869 si opět hrál se svými kartičkami (se jmény prvků) a na půl ucha přitom odvedle poslouchal Schumannův kvintet E dur. V hudbě se tóny stejné zvukové kvality opakují v oktávách… a vida, po osmi se opakují i chemické a fyzikální kvality některých prvků! Idea periodického zákona je na světě.

Před zhruba 120 lety pruský básník, malíř, muzikant a – především lékař Carl Ludwig Schleich debatoval s přáteli o hudbě a technikách jejího provozování. Nad problematikou tlumení tónu klavírním dusítkem pak dostal nápad, který vyústil ve vynález lokální anestézie (v tomto případě infiltrací tkáně a nervových obalů fyziologickým roztokem s příměsí kokainu).

Vědci hudebníci

Láska Alberta Einsteina k housličkám je notoricky známa. Nebyl ale sám, řada vynikajících badatelů měla vřelý vztah k hudbě a někteří na vysoké úrovni hráli na nějaký nástroj či dokonce skládali. Alespoň hrstka příkladů:

Zřejmě nejvýznamnějším hudebníkem mezi vědci byl Alexandr Porfirjevič Borodin, povoláním profesor chemie na lékařské fakultě v Petrohradu (kde už jako student založil amatérskou kapelu). Ve dne přednášel a bádal (objevil řadu chemických reakcí, jeden rozklad organických solí stříbra dodnes nese jeho jméno), po práci komponoval. Velkolepá opera Kníže Igor, premiérovaná tři roky po Borodinově předčasné smrti v roce 1887, dodnes patří k arcidílům světové hudebně-dramatické tvorby.

Nejlepší astronomický pozorovatel konce 18. století William Herschel se přes dvacet let živil jako dirigent, skladatel a učitel hudby; teprve po objevu planety Uran v roce 1781 se u něj astronomie vyhoupla na první místo.

Nejvýznamnější český chirurg konce 19. st. Karel Maydl miloval sborový zpěv, dlouhá léta účinkoval v pražském Hlaholu.

První ze zakladatelů kvantové teorie Max Planck byl vynikajícím klavíristou, během vysokoškolských studií působil v akademickém pěveckém sboru jako sbormistr, sólista a skladatel (v roce 1876 kolegové studenti provedli jeho operetu Láska v lese). Profesuru teoretické fyziky na univerzitě v Berlíně zahájil výzkumem nového typu harmonia. Prací s tímto složitým nástrojem si natolik vytříbil sluch, že jistou dobu mu poslech hudby nepřinášel obvyklé potěšení, protože byl schopen slyšet i ty nejmenší chybičky. Časem tato přecitlivělost (k jeho velké radosti) vymizela.

Na Planckových pravidelných hudebních večírcích zpíval tenor chemik Otto Hahn a na housle hrál Albert Einstein. Všichni tři jmenovaní dostali později Nobelovu cenu.

Nejvýznamnější chemik meziválečného Československa Emil Votoček byl výborným violoncellistou a složil řadu písní a komorních skladeb.

Nu a astronom Bohumil Šternberk, který na sebe upozornil prvním evropským snímkem Pluta po jeho objevu v roce 1930, o pár let později pro Československý rozhlas po svém zhudebnil světlo Vegy, nejjasnější to hvězdy souhvězdí Lyry.