Tři generace matematicko-fyzikálních Bernoulliů

Loni uplynulo 300 let od úmrtí jednoho váženého obchodníka v Basileji. Žil bohabojně podle protestantských zásad, o vědu se nezajímal a přál si, aby z jeho synů vyrostli teologové, právníci, lékaři nebo zdatní obchodníci. Přesto pak s jeho jménem chodilo po světě více slavných a úspěšných vědců – vesměs matematiků a matematických fyziků – než s kterýmkoli jiným. Ten obchodník se jmenoval Nicolaus Bernoulli, žil v letech 1623–1708 a pocházel z rodiny protestantského emigranta z Antverp Leona Bernoulliho, který v 16. století uprchl do Švýcarska před inkvizicí.

Obchodník s kořením a jeho nadané děti

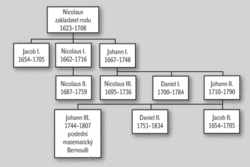
Jacob I. (1654–1705) byl páté dítě svých rodičů a rodiče mu předurčili studium teologie a filozofie. Vzepřel se jejich vůli a vybojoval si možnost studovat astronomii, a hlavně matematiku, které pak věnoval větší část života. Kromě jiných úspěšných výsledků také propočetl křivku nazývanou řetězovka, ¹⁾ jako vůbec první použil (při práci na Newtonově a Leibnizově infinitezimálním počtu) ²⁾ slovo „integrál“ a jako jeden z prvních užíval polární souřadnice. ³⁾ Jako první dokázal zákon velkých čísel, jednu z nejslavnějších vět teorie pravděpodobnosti, jejíž platnost intuitivně tušili nejen matematici, ale i karbaníci a vrchcábníci už dost dávno předtím. Mezi jeho žáky na univerzitě – studenty teologie (!) – byl i mladík jménem Paul Euler, který u Jacoba I. dokonce bydlel v podnájmu. Po vystudování se pastor Euler oženil a měl syna Leonharda. Rodiny Eulerů a Bernoulliů se dál úzce přátelily, a když Leonhard Euler dospěl a začal také studovat teologii, byli to právě mladší Bernoulliové, kteří mu ukázali krásy matematiky a poradili mu změnit obor studia. Otec Paul byl naštěstí rozumný, synovi jeho rozhodnutí nerozmluvil, a tak svět získal jednoho z největších matematiků historie (viz rámeček „Leonhard Euler“ 1 ).

Vraťme se ale k první generaci Nicolausových potomků. Druhý, který se dal na matematiku, byl Nicolaus I. (1662–1716). Ví se toho o něm poměrně málo. Po absolvování univerzity v Basileji se stal profesorem v Sankt Petěrburku. Tím jako první otevřel cestu, po které se alespoň na čas vydala nejen část Bernoulliů, ale i Euler. Nicolaus I. byl sice výborný matematik, věnoval ale skoro všechen čas přednášení, významnějších vědeckých výsledků odvodil jen poměrně málo a věhlasu svých bratrů nedosáhl.

Třetí z matematických Bernoulliů první generace byl Johann I. (1667–1748). Narodil se jako desáté dítě a přes poměrně velký věkový rozdíl přilnul k svému bratrovi Jacobovi I. Podle Jacobova příkladu se i on vzepřel naléhání rodičů a studoval raději matematiku než etiku a teologii, do kterých ho nutili. Zkoumal odraz a lom světla, počítal rovnice složitých křivek a také počítal plochy složitých obrazců sčítáním ploch malých čtverečků, které do nich vepisoval (v době těsně po zvládnutí limit to bylo přitažlivé téma).

Druhá generace slavných

Nicolaus II. (1687–1759), syn Nicolause I., nejspíš studoval a také kromě matematiky vystudoval i práva – soudě podle toho, že jeden čas vedl jejich katedru v Basileji. Mnohem víc ho ale zajímala matematika, které se intenzivně věnoval. Dokonce několik let (před nástupem do Basileje) vedl na univerzitě v Padově katedru založenou kdysi Galileem Galileim. Jako student byl v Basileji pod přímým vlivem obou svých strýců, kteří tam přednášeli. Byl talentovaný, ale nepříliš produktivní autor – jeho objevy je nutné vyhledávat většinou v soukromé korespondenci, kterou vedl hlavně se svým přítelem Leonhardem Eulerem a se slavným Leibnizem (její katalog zahrnuje 560 položek). Zabýval se geometrií a diferenciálními rovnicemi a nezávisle na svém strýci Jacobovi I. a na Leibnizovi odvodil jeden ze vzorců pro výpočet desetinných hodnot čísla π pomocí nekonečných číselných řad.

Nejmladší ze tří bratrů první generace, Johann I., přispěl k matematické dynastii hned třemi potomky. Je pozoruhodné, že se Johann I. nepoučil z vlastní zkušenosti a všechny své syny přiměl vystudovat vedle matematiky i „praktičtější“ obory. Právě jeho by nemělo překvapit, že je hned po absolvování víceméně pověsili na hřebík.

První z jeho synů, kteří se proslavili, byl Nicolaus III. (1695–1726). Byl prý Johannovým nejoblíbenějším synem a zřejmě byl mimořádně nadaný – na univerzitu (do přípravky) nastoupil už ve třinácti letech a současně s matematikou studoval také práva. Po absolvování pak nastoupil jako otcův asistent. V té době ještě mezi matematiky probíhala vzrušená diskuse o prvenství v objevu diferenciálního a integrálního počtu (viz rámeček „Spor o prvenství“ 3 ) které se Nicolaus III. zúčastnil a při shromažďování argumentů postupně objevoval zajímavé vlastnosti složitých křivek a trajektorií funkcí. Několik nových vět přidal i k teorii pravděpodobnosti. Krátce před třicítkou přijal profesorské místo v Sankt Petěrburku, nepochybně i pod Eulerovým vlivem. Poměrně brzy po nástupu ale onemocněl a zemřel dřív, než mohl svůj nesporný talent rozvinout naplno.

Další Johannův syn, Daniel I. (1700–1784), by mohl být hodně vážným kandidátem na pozici nejslavnějšího z Bernoulliů. Otec ho sice nutil k dráze kněze nebo obchodníka, on si ale prosadil vstup na univerzitu a stejně jako jeho starší bratr na ni byl přijat ve třinácti letech. Po filozofické přípravce nastoupil studium medicíny, ve skutečnosti ho ale mnohem víc zajímaly matematika a fyzika. Když se otec Johann I. smířil se synovou vzpourou, začal ho sám oba obory učit a přibral ho i ke svým výzkumům kinetické energie. Tak se stalo, že Daniel úspěšně dokončil studium medicíny prací o energii dýchání. Jako matematik byl pozoruhodně všestranný. Ještě pod otcovým vlivem dokázal, že chvění struny je součtem nekonečně mnoha harmonických kmitů. Bývá také označován za „otce matematické fyziky“ a známý Bernoulliho zákon o proudění kapalin a plynů je jeho objevem. Podstatně přispěl k rozvoji teorie pravděpodobnosti ⁴⁾ a jeho článek o takzvaném „petěrburském paradoxu“ (viz rámeček „Petěrburský paradox“ 2 ) vlastně založil matematickou teorii užitku, a tím i výzkum matematických modelů ekonomických jevů. Několik let působil v Sankt Petěrburku, kde sice rád spolupracoval s rodinným přítelem Eulerem, ale zároveň na něj tísnivě působila vzpomínka na bratra, který tam před časem zemřel. Proto se raději vrátil do Basileje a získal tam uvolněné profesorské místo. Byl vystudovaný lékař, a tak nás ani moc nepřekvapí, že bylo na biologii – všestrannosti na to měl dost. Stejně ale zaměřil hlavní pozornost na matematické modely fyzikálních jevů, hlavně na hydrodynamiku se vztahem k zákonu zachování energie. Zajímal se také o elektrické jevy, které tehdy začínaly budit pozornost, a dokonce odvodil matematický vzorec pro Coulombův zákon, do té doby pozorovaný jen experimentálně.

Třetí z Johannových synů, kteří se uplatnili v matematice, byl Johann II. (1710–1790). Některými životopisci bývá za nejúspěšnějšího člena rodu pro změnu označován on, patrně měřeno společenským postavením a poctami. I on začal tím, že úspěšně vystudoval práva, ale nezůstal u nich a prakticky hned po absolvování přeběhl k matematice. Byl to skoro jistě on, kdo měl největší zásluhu na získání Leonharda Eulera pro matematiku. Jeho vlastní matematický výzkum měl hodně blízko k fyzice. Nějakou dobu i on spolupracoval s otcem, pak po něm zdědil katedru matematiky a v klidu se zabýval diferenciálním počtem a jeho využitím v modelech šíření tepla a světla. Ze tří synů Johanna I. byl jediný, který po sobě zanechal matematicky nadané potomky.

Poslední Bernoulliové

Jacob II. (1759–1789) se nedožil vysokého věku. Po vzoru otce vystudoval práva, a pak se věnoval matematické fyzice. Ucházel se o vedení katedry uvolněné v Basileji strýcem Danielem (po jeho odchodu do Sankt Petěrburku), ale o místo se losovalo a Jacob II. prohrál. Brzy nato i on dostal nabídku na lukrativní místo v Petěrburku. Lákala ho možnost pracovat spolu se strýcem a s Eulerem, a tak ji přijal. Pilně pracoval, publikoval články o matematické fyzice, hlavně o pružnosti, hydrodynamice a balistice, a dokonce se i oženil – vzal si Eulerovu vnučku, čímž se přítel Leonhard stal příbuzným Bernoulliů. Jacob II. byl nejspíš fyzicky zdatný a otužilý člověk – pravidelně chodil plavat do Něvy, která v Petěrburku není příliš teplá ani v létě. Jednou přecenil své síly a v nedožitých třiceti letech se utopil.

Zbývá Johannův poslední syn. Johann III. (1744–1801) se sice narodil jako první z bratrů, ale přežil Jacoba II. a při značné spornosti matematických zásluh Daniela II. je všeobecně považován za posledního žijícího matematika s příjmením Bernoulli. Jeho život budí trochu rozpaky a trochu i nostalgii nad soumrakem slavného rodu. Přitom začínal velmi slibně – byl považován za zázračné dítě, ve čtrnácti letech byl přijat na univerzitu a v devatenácti ji dokončil. Je skoro zbytečné dodávat, že jako doktor práv, ale že se i on začal hned po absolvování věnovat matematice. Rychle získal dobrou pozici v berlínské Akademii a byl považován za slibný matematický talent, kterým nejspíš také byl. Tehdy se na něj obrátil pruský král Bedřich I. s žádostí, spíš pokynem, aby oživil berlínskou astronomickou observatoř. Johann byl poslušný a věrný poddaný a pustil se do práce, která svou podstatou moc neladila s jeho naturelem. Observatoř skutečně uvedl do chodu a organizoval astronomický život ve větší části Německa. Články, které publikoval, byly vesměs o astronomických pozorováních a jejich matematickém zpracování. Sepsal je pečlivě a přesně, ale nebyla to ta věda, která by ho lákala. Teprve v zbývajícím čase psal matematické publikace, vesměs o teorii rovnic a rekurentních desetinných zlomcích. Nebyly bezvýznamné, ale od člověka s jeho jménem se čekalo víc. Dnes jsou z jeho pozůstalosti nejvíce ceněny zápisky z cest po německých hvězdárnách – využívají je historici vědy. Johann III. byl dost inteligentní na to, aby pochopil, že jím se matematický věhlas rodu Bernoulliů uzavírá, a dovedl z toho vyvodit závěry. Věnoval hodně sil hledání korespondence, kterou vedli jeho předci a příbuzní. Shromáždil několik tisíc dopisů, které pak prodal Švédské akademii věd. ⁵⁾

Sklony k matematice se přenášejí

Dvojic matematiků tvořených otcem a jeho potomkem (většinou synem, ale někdy také dcerou) je v historii zaznamenáno poměrně hodně – sklony k matematice se často mezi generacemi přenášejí. Po Bernoulliových tvořili druhou největší „rodinnou skupinu“ asi Pythagoras, jeho žena Theano a jejich dcery Myia a Damo. Je sporné, i když možné, že k nim patřil i Pythagorův tchán Milon, několikanásobný olympijský vítěz a král Krotonu. Zdá se to být dost lidí, ale vedle tří generací Bernoulliů se taková skupina nutně vytrácí, a chceme-li sáhnout i mimo matematiku, pak i rodiny Straussů v hudbě nebo Mánesů ve výtvarném umění vypadají najednou trochu vylidněné.