Kvazikrystaly

Co je to krystal

Pro většinu z nás je typickým znakem krystalu jeho tvar. Krystaly jsou omezené krystalovými plochami. Různé látky krystalizují v různých, ale pro jednotlivé látky typických tvarech. Například sůl krystalizuje téměř vždy v krychlích, ledové krystaly známe zase v podobě šesticípých vloček. Tyto tvary jsou ale odrazem vnitřní stavby krystalu, a z hlediska chemického a fyzikálního je právě vnitřní stavba na úrovni atomů tím, co odlišuje krystaly od jiných forem látek.

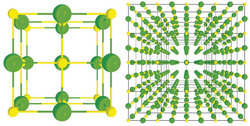Pro pochopení struktury krystalů byl klíčový objev rentgenového záření na sklonku 19. století. Nedlouho poté, v roce 1912, provedl Max von Laue se svými dvěma spolupracovníky W. Friedrichem a P. Knippingem průlomový experiment, při kterém nechal na krystal síranu měďnatého dopadat rentgenové záření. Analýzou obrazce vzniklého rozptylem záření na krystalech dokázal, že ozařovaný krystal je tvořen trojrozměrně periodickým opakováním obrovského množství maličkých jednotek, tzv. základních buněk. Každá taková buňka má velikost okolo jednoho nanometru (připomeňme 1 nm = 10^–9 m, je to tedy tisícina mikrometru), a není to pevné těleso, ale pouze myšlená část prostoru vyplněná přesně definovaným seskupením jednotlivých atomů (obr. 1).

Opakování tohoto experimentu na dalších krystalech ukázalo, že tento princip je univerzální, a zdálo se, že takto lze popsat všechny krystaly a že právě tato vlastnost je odlišuje od jiných způsobů uspořádání látek, jako jsou například sklo nebo vosk. Sklo a vosk patří mezi látky označované jako amorfní a uspořádání atomů a molekul v nich není přesně určeno jako v krystalech, ale je do značné míry náhodné.

Trojrozměrně periodické uspořádání atomů bylo tedy považováno za základní princip výstavby krystalických látek. Pro názornost si jej demonstrujme na dvojrozměrném příkladu. Obr. 2 ukazuje několik různých způsobů, jak periodicky vyplnit plochu pomocí jedné „dlaždice“, tedy jedné základní buňky. Poslední obrázek ukazuje, že ne každým geometrickým tvarem lze plochu beze zbytku vyplnit. Pokud chceme použít základní buňku tvaru pětiúhelníku, zbudou nám při vyplňování plochy prázdná místa, a výsledný obrazec navíc nebude periodický. Je možné dokázat, že z pravidelných mnohoúhelníků lze plochu beze zbytku vyplnit pouze čtvercem, trojúhelníkem a šestiúhelníkem. Proto krystaly nemohou mít pětičetnou a více než šestičetnou souměrnost, přestože pětičetná souměrnost je tak běžná v rostlinném světě.

Není to periodické, ale není to neuspořádané – co to je?

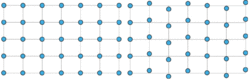Kvůli malým rozměrům základních buněk běžných krystalů dlouho neexistoval způsob, jak strukturu krystalů pozorovat přímo, a proto vždy byla a dodneška je základní metodou jejich výzkumu difrakce (tedy rozptyl a následná interference) rentgenového záření, neutronů nebo elektronů na krystalech. Jak už bylo řečeno, analýzou difrakčních obrazců bylo možné dokázat, že krystaly jsou periodické, a pomocí difrakce je také možné zjistit přesné uspořádání atomů v základních buňkách. Po nějakém čase byly objeveny krystaly, jejichž difrakční obrazce naznačovaly, že jejich struktura není přesně periodická. Těmto strukturám se dnes říká modulované, a přestože se o jejich existenci vedly diskuse a teorie umožňující jejich přesný popis byla vyvinuta až na sklonku sedmdesátých let 20. století, neznamenal jejich objev zásadní ránu pro paradigma periodicity krystalů. Tyto struktury si totiž lze představit jako periodické struktury s dodatečným malým, přesně definovaným narušením (obr. 3). Zásada, že krystaly nemohou mít pětičetnou a více než šestičetnou symetrii, zůstala platná i pro modulované struktury a zdála se být neotřesitelným pravidlem rovným bezmála fyzikálnímu zákonu.

Dan Shechtman se ve svém výzkumu zabýval slitinami kovů vzniklých náhlým ochlazením jejich taveniny. Protože rozměry takto vzniklých krystalů byly příliš malé pro výzkum rentgenovým zářením, zkoumal je pomocí difrakce elektronů v elektronovém mikroskopu. V roce 1982 ke svému překvapení nalezl ve slitině hliníku s manganem opakovaně krystaly, jejichž difrakční obraz obsahoval desetičetné osy a ukazoval na ikosaedrickou souměrnost krystalu (obr. 4).

To bylo natolik v rozporu s obecně uznávanými principy, že tomu nejprve ani sám Shechtman nechtěl věřit. Proto provedl sérii experimentů, jimiž se pokusil nalézt alternativní vysvětlení, ale výsledkem bylo pouze potvrzení dřívějších závěrů: tento materiál je perfektně uspořádaný, ale obsahuje „zakázanou“ pětičetnou souměrnost, a proto nemůže být periodický. Své závěry publikoval v roce 1984.

Není překvapivé, že s takto zásadním tvrzením Dan Shechtman u ostatních vědců z krystalografické komunity narazil. Trvalo nějakou chvíli, než jej alespoň někteří začali brát dostatečně vážně na to, aby se pokusili jeho výsledky potvrdit nebo vyvrátit. K překvapení všech se ukázalo, že Danem Shechtmanem objevené materiály, které byly nazvány kvazikrystaly, nejen existují, ale že jich existuje mnoho typů a lze je nalézt v mnoha slitinách, a to jak binárních, jako jsou namátkou Mn–Si, Al–Mg, Cd–Yb nebo Cr–Ni, tak ternárních, například Al– Co–Ni, Al–Mn–Pd nebo Pd–U–Si. Některé kvazikrystaly jsou metastabilní, ale jiné jsou za určitých podmínek termodynamicky stabilní a lze z nich vypěstovat i několik centimetrů velké, perfektně vyvinuté krystaly (obr. 5).

Jak vypadá struktura kvazikrystalu?

Kvazikrystaly jsou charakteristické tím, že jsou perfektně uspořádané, ale neperiodické. Uspořádaná struktura je – volně řečeno – vystavěna podle určitého předpisu tak, že známe- li tento předpis a jistou malou část struktury, jsme schopni určit, jak bude struktura vypadat na kterémkoli jiném místě krystalu. Periodické krystaly tuto podmínku splňují. Známe-li základní buňku, víme, že celý krystal můžeme „postavit“ naskládáním těchto buněk vedle sebe ve všech třech rozměrech. Lze ale dosáhnout uspořádanosti bez periodicity?

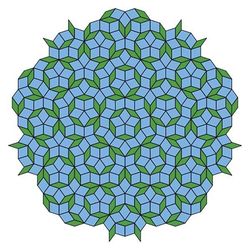
Odpověď na tuto otázku není zdaleka zřejmá a byla předmětem teoretických úvah matematiků dlouho před objevem kvazikrystalů samotných. Podařilo se dokázat, že uspořádanost bez periodicity možná je. Zřejmě nejznámějším příkladem je tzv. Penroseovo dláždění. Toto dláždění bylo objeveno britským fyzikem sirem Rogerem Penrosem (podle jeho vlastních slov se tímto problémem začal zabývat, když musel pobývat nějakou dobu v nemocnici a poněkud se tam nudil) a jeho nejznámější verze je tvořena dvěma různými kosočtverci (obr. 6). Dláždění má pětičetnou souměrnost. V trojrozměrném prostoru lze zkonstruovat analogii Penroseova dláždění, ve které dva různé klence (krychle zploštělé podle jedné úhlopříčky) vyplňují beze zbytku celý prostor. Do doby, než byly objeveny kvazikrystaly, bylo Penroseovo dláždění a podobné konstrukce považovány za pouhé matematické hříčky.

Po objevu kvazikrystalů nastal boom jejich výzkumu. Několik laboratoří po světě se snažilo nejen nalézt kvazikrystaly v dalších a dalších slitinách nebo jiných materiálech, ale především popsat a pochopit jejich strukturu. Ukázalo se, že kvazikrystaly lze rozdělit do dvou základních skupin.

Ikosaedrické kvazikrystaly, mezi které patří i „Shechtmanovy“ kvazikrystaly v systému Al–Mn, jsou neperiodicky uspořádané ve všech směrech a mají ikosaedrickou souměrnost, tedy stejnou souměrnost, jako má ikosaedr nebo dvanáctistěn pětiúhelníkový (obr. 5). Dalším typem jsou kvazikrystaly s neperiodickým uspořádáním pouze ve dvou rozměrech. Takovéto kvazikrystalické roviny jsou potom periodicky naskládány na sebe, a v rámci kvazikrystalické roviny mají osmičetnou, desetičetnou nebo dvanáctičetnou souměrnost. Struktury všech těchto kvazikrystalů lze popsat pomocí dvou nebo více základních buněk, které jsou poskládány tak, že vyplňují prostor nebo rovinu uspořádaně, ale neperiodicky, podobně jako Penroseovo dláždění. Alternativně lze tyto struktury popsat pomocí pouze jedné „základní buňky“ – přesněji atomového motivu – který je poskládán tak, že se části sousedících motivů překrývají.

Objev kvazikrystalů a vysvětlení jejich struktury znamenaly zásadní zvrat v našem chápání fundamentálních principů řídících uspořádání atomů v pevných látkách. Zároveň také vzbudily velká očekávání. Vědci doufali, že nové uspořádání atomů s sebou přinese nové, nečekané fyzikální vlastnosti a následně nové a nečekané aplikace těchto materiálů. S postupujícím výzkumem se ovšem ukázalo, že kvazikrystaly nemají žádnou zásadní fyzikální vlastnost, kterou by neměly i nějaké jiné materiály. Je ovšem pravda, že kvazikrystaly se mohou pochlubit velmi neobvyklou kombinací fyzikálních vlastností. Přestože jsou složeny pouze z kovů, jsou velmi dobrými tepelnými a elektrickými izolátory. Závislost jejich elektrické vodivosti na teplotě je navíc obrácená než u kovů – se vzrůstající teplotou stoupá. Na rozdíl od čistých kovů jsou také velmi tvrdé a odolné proti korozi, a mají nízký koeficient tření.

Tato kombinace vedla k návrhu několika zajímavých aplikací. Nejznámější je zřejmě využití kvazikrystalů jako materiálu pro povrchové vrstvy kuchyňských pánví. Takto ošetřené povrchy se chovají podobně jako teflonové, ale jsou odolné proti poškrábání. Výroba těchto pánví byla ale pozastavena poté, co se ukázalo, že za určitých okolností může materiál povrchové vrstvy reagovat s kuchyňskou solí a způsobovat nežádoucí uvolňování kovů do potravin.

Mezi další zajímavé aplikace patří využití kvazikrystalů místo jiných kovových slitin při ukládání vodíku do vodíkových článků. Kvazikrystaly ze systému Ti–Zr–Ni mají proti jiným kovům a slitinám (Pd, La–Ni, Mg– Ni) výhodu, že jsou relativně levné a mají relativně vysokou absorpční kapacitu. Jejich nevýhodou je, že při opakované absorpci a desorpci vodíku dochází k reakci kovů s vodíkem za vzniku hydridu a materiál se rozpadá. Zřejmě nejvýznamější a jedinou šířeji využívanou aplikací kvazikrystalů je tak jejich přítomnost ve formě mikro- a nanokrystalů ve speciálních ocelích. Kvazikrystalické částice takovýmto slitinám propůjčují tvrdost a houževnatost a obzvláštní odolnost proti korozi. Tato ocel se používá především pro výrobu chirurgických nástrojů, ale také pro výrobu břitů pro některé holicí strojky značky Philips.

Závěr

Objev kvazikrystalů zásadně změnil pohled chemiků a fyziků na základní principy uspořádávání látek na atomární úrovni. Dříve panující představa, že periodicita je univerzálním principem platným pro růst všech krystalů, musela být opuštěna a nahrazena novým, obecnějším pohledem. Situace byla podobná objevu obecné teorie relativity. I tato teorie zobecnila Newtonovy gravitační zákony a změnila náš pohled na fungování gravitační síly, o které jsme si mylně mysleli, že ji dobře chápeme. Ale stejně jako Newtonovy zákony pořád využíváme ve velké většině každodenních aplikací, i periodicita běžných krystalů nadále zůstává užitečným pomocníkem pro každodenní práci vědců s krystalickými materiály. Komplikované výpočetní postupy nutné pro analýzu kvazikrystalů – stejně jako komplikovanou teorii relativity – používáme jen tam, kde se bez nich neobejdeme. To ovšem nemění nic na tom, že objev kvazikrystalů patří k těm několika průlomovým objevům, které nás nechávají v úžasu stát nad elegancí, se kterou příroda dokáže znovu a znovu rozmetat naši naivní víru v to, že jsme už alespoň některá její tajemství úplně pochopili.