Mohou zmoknout vlny?

Položme si poněkud dětinskou otázku: Mohou zmoknout vlny? Máme na mysli vlny elektromagnetické, zvláště těch vlnových délek, které se běžně používají při provozu mikrovlnných spojů v sítích mobilních operátorů i pro mnoho služeb dalších. Odpovězme s trochou nadsázky, že vlny skutečně zmoknout mohou, a naznačme, že nám jde o rozptyl vln na jednotlivých kapkách deště, s nímž je spojena řada efektů.

Nejprve se zmíním o jevu, který mohli pozorovat již naši předkové od dob, kdy je Země Zemí. Mám na mysli obyčejnou duhu. Určitě jsme všichni nejednou viděli, jak různě se rozptylují jednotlivé vlnové délky světla – od těch nejdelších (červených) přes žluté, zelené, modré až po nejkratší viditelné (fialové). Mnohý z nás si vzpomene i na „dvojí duhu“, kdy vedle zřetelného hlavního pruhu barev objevil další, slabší, a při velkém štěstí možná někdo zahlédl i třetí barevnou „stuhu“.

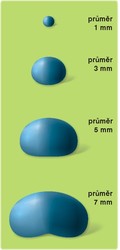
Ačkoliv nám jsou tyto jevy srozumitelné, usilovaly o jejich vysvětlení generace fyziků, včetně Isaaca Newtona. Uspokojivé vysvětlení přineslo až 20. století. Analyticky odvodil řešení diferenciálních rovnic pro rozptyl na sféře německý matematik Gustav Mie již roku 1908. Po dlouhou dobu však jeho řešení představovalo jediný možný způsob. V duchu mieovského rozptylu se nejdříve uvažovala náhrada dešťových kapek kulovými objekty různých velikostí. Teprve později bylo možné uvažovat zploštělý elipsoid, a potom i skutečné tvary dešťových kapek, jejichž model vytvořili r. 1971 na základě fotografických studií Pruppacher a Pitter (viz obr. obrázek). Odpověď na řadu otázek však byla nalezena až na základě simulací, které umožnil nástup výpočetní techniky a rozvoj numerických metod.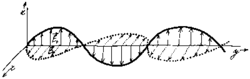

Stejně jako bylo pro fyziky minulých generací tvrdým oříškem vysvětlení dalších maxim rozptýleného světla (dalších duh), bylo možné i u radiových vln vysvětlit řadu dnes pozorovatelných jevů pouze natolik, nakolik to dovolovaly možnosti královny věd – matematiky. Také v případě mikrovlnných spojů bylo třeba vyjít ze zjednodušení, která již z principu vyřadila množství dnes známých jevů. Proč je za deště útlum horizontálně polarizovaného signálu vyšší než útlum signálu s polarizací vertikální? Proč vznikají (zvláště za silného deště, kdy je výskyt nesymetrických kapek vyšší) přeslechy mezi signálem vysílaným v jedné a druhé polarizaci? – To je jen ukázka otázek, které nelze zodpovědět, pokud zanedbáme skutečné tvary dešťových kapek.

Analogie mezi rozptylem světla s efektem duhy a rozptylem elektromagnetických vln řádu GHz je však nasnadě, přestože u světla jde o rozptyl celé škály kmitočtů (námi pozorovaných barev), kdežto u spojů mikrovlnných sledujeme kmitočet jediný. Navíc jsou vlnové délky světla mnohem kratší (400–800 nm) než u elektromagnetických vln, řádově centimetrových. Velikosti dešťových kapek jsou vzhledem k vlnovým délkám světla také mnohem větší než v případě „rádiových“ kmitočtů, kdy vzhledem k zkrácení vlnové délky uvnitř kapky může jít o rozměry řádově srovnatelné. Logicky lze proto očekávat, že i charakter (tvar) rozptýleného pole u světla (poloha jednotlivých maxim) bude jiný než u pole rozptýlené rádiové vlny.

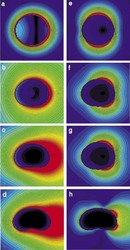
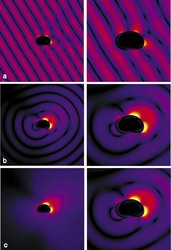
Označme však obecně rozptylem elektromagnetické vlny jev, kdy se mění charakter šířící se vlny díky interakci s anomálií prostředí (objektem kapky). Pole dopadající rovinné vlny (viz obr. ) se stává polem zdrojovým pro pole vnikající do kapky i pro pole rozptýlené, přičemž jsou respektovány podmínky na rozhraní. Prostředí kapky popisujeme permitivitou, permeabilitou a vodivostí. Pro jednoduchost si představme, jako by každá kapka byla vybuzena šířící se vlnou v jakýsi elementární dipól, jehož vyzařovací charakteristika závisí na intenzitě dopadající vlny, na tvaru a prostředí dešťové kapky a na poměru vlnové délky vzhledem k rozměrům kapky. Pro kmitočty mikrovlnných spojů platí, že v prvním přiblížení lze uvažovat vyzařovací charakteristiky jednotlivých kapek ve tvaru jakýchsi anuloidů tak, jak to známe pro elementární dipól z teorie antén či ze základů fyziky.

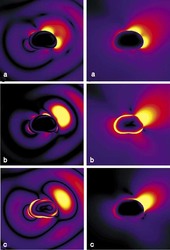
Vzhledem ke skutečnosti, že pole rozptýlené je o mnoho řádů slabší než původní pole vlny dopadající, lze zanedbat rozptyly vyšších řádů (rozptyl už jednou rozptýleného pole) a uvažovat výsledný rozptyl jako součet účinků jednotlivých dešťových kapek. Vyřešením rozptylu pro kapky všech velikostí (obr. ) se tak otevírá cesta k „makroskopickému“ pohledu na úlohu rozptylu.

Tam je podstatné především správné vymezení oblasti deště a jejího průniku s trasou spoje a co možná nejvěrnější znalost výskytu kapek různých velikostí v dešti dané intenzity, tzv. spektrum DSD (Drop Size Distribution). Pak už nic nestojí v cestě např. výpočtu interferencí mezi stanicemi jednotlivých služeb, stanovení možného úniku na trase mikrovlnného spoje nebo třeba určení odraženého výkonu v radarové meteorologii. ¹⁾