Kvantové počítače
Již od dob prvních prototypů se rychlost počítačů každým druhým rokem zhruba zdvojnásobí, a to při současném dvojím zmenšení a zahuštění elementárních součásti. Za padesát let úsilí o stále miniaturnější a kondenzovanější počítače se tak lidstvo dostalo od elektronkových obrů konce čtyřicátých let, vyplňujících (a nechtěně též vyhřívajících) prostorné sály, až k symbolu naší doby – notebooku založenému na integraci polovodičových komponent mikroskopických rozměrů. A protože počítač je ve své podstatě jen fyzikální přístroj, není divu, že snaha o další vývoj nutila a nutí počítačové technology zabývat se stále novými fyzikálními problémy. Kde dříve stačila klasická elektrodynamika s popisem založeným na spojitě se měnících hustotách nábojů a proudů, tam se nyní nelze obejít bez představy jednotlivých elektronů procházejících krystalickou mříží atomů polovodiče.
Jak víme, svět mikročástic však řídí jiná mechanika, než jakou známe z všední zkušenosti, a to mechanika kvantová. Přestože mnohé z vývodů kvantové teorie si už našly cestu i do počítačových technologií, její využití je stále spíše okrajového rázu. Hlavní idea, na níž stojí dnešní počítače, totiž zůstává od dob svého vzniku téměř nezměněna. V podstatě jde stále jen o elektrický obvod, byť nyní již velmi důmyslným způsobem ovládaný integrovanými prvky mikronových velikostí. Co se však stane, dostaneme-li se neustálým zmenšováním až na hranici tisícinásobně větší integrace, než jaké jsme schopni dosáhnout dnes? Elektronické součásti budou potom rozměrů pouze desítek až stovek atomů a kvantová teorie nabude vrchu nad obvyklým klasickým popisem. Teorie elektrických obvodů přestane na těchto škálách platit, což si v konečném důsledku vynutí přehodnocení základních principů klasických počítačů.
V čem ale spočívá ta zásadní odlišnost světa kvant od našeho makroskopického světa, která nutí konstruktéry počítačů zabývat se mezemi použití klasických přístupů? Na první pohled se jí zdá být právě kvantování fyzikálních veličin – např. energie elektronu vázaného v atomu nabývá jen určitých diskrétních hodnot na rozdíl od klasického spojitého spektra energií; nejmenším rozdílům energií hladin se říká kvanta, odtud také název kvantová fyzika. Hlubší rozdíl však tkví v existenci na klasické úrovni nepoznaných stavů hmoty, tzv. superpozic. Zkusme toto slovo, ve fyzikálním jazyce již zdomácnělé, vysvětlit na jednoduchém příkladě.
Jak jsme již řekli, elektron se může v atomu vodíku vyskytovat ve stavech, kdy je jeho energie dobře definovanou veličinou vztahující se, jak vědí čtenáři obeznámení s fyzikální chemií, k hlavnímu kvantovému číslu (vzpomeňme na hodiny chemie a na vyplňování okének šipkami, jež představují jednotlivé elektrony v obalu atomu). Kvantová teorie však pracuje též se stavy, právě zmíněnými superpozicemi, jež jsou složením nebo – řečeno více matematicky – váženým součtem několika různých stavů (odtud také slovo superpozice, superponován – naložen jeden na druhý). A zde se dostáváme k vlastnostem, jež nemají na klasické úrovni obdoby. Pro elektron v superpozici stavů s různou energií totiž nemá pojem jeho vlastní energie úplně dobrý smysl (jeho stav neodpovídá žádné z energetických hladin v atomu). To se samozřejmě projeví i při pokusech jeho energii změřit, kterými se dopracujeme tu k hodnotě jednoho, tu k hodnotě jiného stavu vystupujícího v superpozici. Výsledky měření mají přitom zcela náhodný charakter (lze je dokonce užívat jako ideální náhodný generátor), a tedy nejsou předvídatelné! Jediná předpověď, kterou je v takovém případě kvantová teorie schopna dát, se týká statistiky rozložení výsledků, jež je přitom jednoznačně svázána se způsobem smíšení uvažovaných stavů.
Podle kvantové teorie je měření náhlým a nevratným zásahem do evoluce systému. Zatímco se izolovaný kvantový systém vyvíjí hladce a deterministicky, v okamžiku měření se jeho stav nevyhnutelně drasticky změní (tzv. redukce vlnového balíku). Superponovaný stav přechází na stav odpovídající té konkrétní (nicméně jednoznačně nepředvídatelné) hodnotě, která byla v experimentu změřena. Jak uvidíme dále, tato vlastnost kvantového měření má pro počítače využívající kvantových principů velmi závažné negativní důsledky.
Obraťme se však nyní zpět do světa výpočetní techniky a povězme si, co bylo kromě úvah technologů o hranicích použitelnosti tradičních konceptů příčinou zájmu počítačových teoretiků o kvantovou mechaniku. V principu šlo o dva hlavní zdroje. Na počátku prvního z nich stály jisté termodynamické úvahy o energetické bilanci výpočetního procesu, které postupně vykrystalizovaly v názor, že se během každého elementárního kroku (tj. základní logické operace), který data během výpočtu podstupují, nutně vyloučí určité minimální množství tepla (či přesněji vzroste entropie systému o jistou minimální hodnotu). Vyloučené teplo musí být odváděno, aby se předešlo poškození choulostivých součástí elektrických obvodů. To však pro příliš rychlý či příliš integrovaný počítač není z principu možné, což může vést k výraznému omezení další miniaturizace.Zmíněné pesimistické předpovědi byly vyvráceny teprve až na konci sedmdesátých let návrhem počítače, jenž pracuje fyzikálně vratným způsobem (připomeňme, že vratnost znamená, že i obrácený fyzikální děj je možný – film běžící pozpátku pak ukazuje jevy stejně logické jako film normální). Je zajímavé, že práce popisovaného modelového stroje byla založena na tak jednoduchých fyzikálních jevech, jakým je ráz kulečníkových koulí (odtud také název billiard-ball computer), jehož reverzibilita je evidentní. Je zcela přirozené, že úvahy o systematickém využití vratnosti fyzikálních zákonů klasické mechaniky vedly posléze k jejich rozšíření i na mechaniku kvantovou.
Druhý podnět k zapojení kvantové fyziky do výpočetních procesů dal americký fyzik Richard Feynman, který si při rozboru teoretických aspektů simulací kvantových systémů na klasických počítačích všiml, že nároky na výpočetní čas rostou geometrickou řadou v počtu stupňů volnosti kvantového systému (každý stupeň volnosti odpovídá jedné z nezávislých souřadnic systému – např. jedna klasická částice má 3 stupně volnosti, dvě částice pak 6, tři 9 atd.). S jasnozřivostí jemu vlastní vyslovil Feynman obrácenou hypotézu, že simulace výpočtu klasického počítače pomocí cílené evoluce nějakého vhodného kvantového systému může vést k podstatnému urychlení běhu některých algoritmů.
Od výše zmíněných pionýrských prací byl už jen krok k definici kvantového počítače, předložené oxfordským matematikem Davidem Deutschem v práci z r. 1985 (tenkrát ještě zcela osamocené). Podle ní je kvantovým počítačem fyzikální systém, jehož určité kvantové stavy (např. stavy odpovídající energetickým hladinám) kódují klasické logické (booleovské) hodnoty (nuly a jedničky) a jehož spontánní časový vývoj odpovídá provádění určitého výpočetního algoritmu. Na první pohled se Deutschův počítač nezdá být příliš odlišný od klasických (vratných) strojů, hlubší rozbor však odhalí podstatné rozdíly:
Kvantový počítač je svébytný kvantový systém, jehož logické stavy nejsou jenom typu ANO – NE, jak jsme zvyklí, ale též jejich libovolné superpozice. To vede k pojmu kvantový bit – qubit, jakožto analogie klasického dvouhodnotového bitu. Ve stejné paralele odpovídají klasickým hradlům provádějícím operace NOT, X-OR apod. hradla kvantová, která mění stavy qubitů prostřednictvím spontánní kvantové evoluce. Zmíněná spontánnost časového vývoje znamená především jeho nerušenost – při výpočtu na kvantovém počítači např. nelze odečítat mezivýsledky (tj. měřit okamžitý stav počítače), aniž by se tím samotný výpočet drasticky neovlivnil!
Přes všechen teoretický průlom popsaný v předchozích odstavcích by celá problematika zřejmě nikdy neopustila pole akademických diskusí, kdyby nebylo práce z přelomu roků 1993/94, potvrzující Feynmanovu hypotézu o nečekaných výpočetních schopnostech kvantových počítačů. Tato práce, v níž Peter Shor z Bellových laboratoří v New Jersey předložil řešení klasického problému faktorizace velkých čísel na prvočíselný rozklad pomocí kvantového počítače, odstartovala skutečnou explozi článků na téma kvantových počítačů a jejich praktické realizace, jíž jsme v posledním dvouletí svědky.Oč v problému faktorizace jde? Představme si, že někdo vynásobí dvě prvočísla, oznámí nám svůj výsledek, a pak nám dává hádat, jaká prvočísla to byla. Přes jednoduchost zadání je tato úloha již od klasických dob (vzpomeňme Erathosténovo síto, viz J. Fiala, Vesmír 72, 605, 1993/11) tvrdým oříškem, a to zvláště, jsou-li obě prvočísla velká. Nejlepší současný klasický algoritmus dokáže nalézt jednoho z dělitelů takového složeného čísla o L cifrách za čas úměrný exp(L1/3), tj. za exponenciálně dlouhý čas (jak o tom psal Pavel Pudlák ve Vesmíru 74, 305, 1995/6), kdežto Shorův algoritmus je téhož schopen za čas velikosti La, kde a je malé přirozené číslo větší než dvě, tj. za čas pouze polynomiální v počtu cifer L. Srovnání obou časů vede pro velká L (tj. L větší než řádově tisíc) k přesvědčivému vítězství kvantového počítače.
Byť se to asi nezdá, celá věc má i jeden velmi praktický aspekt: údajná nemožnost rozkladu velkých čísel v rozumném čase totiž umožnila takzvané veřejné kódy: k zašifrování informace se používá prvočíselného dělitele čísla o řádově stovce platných míst, který z veřejně přístupného součinu odvodí (a s jeho pomocí např. uskuteční bankovní převod mezi tímto kódem chráněnými účty) jen ten, kdo zná druhý faktor. Je tedy jasné, že popsaná kryptografická metoda je zajímavá nejen pro Pentagon, ale třeba i pro velké banky1). Díky Shorově řešení tak kvantové počítače vlétly takřka po hlavě přímo do problematiky nezanedbatelné praktické důležitosti.
 Proč jsou však kvantové počítače potenciálně výkonnější než jejich klasické protějšky? Řešení se skrývá v zachovávání vah stavů v superpozicích během kvantového výpočtu, vyplývajícím z linearity kvantové evoluce. Předpokládejme, že máme před sebou tabulku čísel, pro něž máme za úkol provést určitou proceduru. Klasicky bychom museli procházet tabulku a výsledky vyčíslovat hodnotu po hodnotě. Kvantová evoluce nám naopak umožňuje provést tuto kalkulaci pro všechny vstupní hodnoty najednou. Připravíme-li totiž na vstup počítače stav, jenž je lineární kombinací stavů kódujících všechny hodnoty z tabulky, a provedeme výpočet, obdržíme stav, který je obdobnou lineární kombinací všech výstupních hodnot! Popsaná vlastnost, tzv. kvantový paralelizmus, nemá obdoby v klasickém světě, jelikož se podstatně opírá o existenci kvantových superpozic.
Proč jsou však kvantové počítače potenciálně výkonnější než jejich klasické protějšky? Řešení se skrývá v zachovávání vah stavů v superpozicích během kvantového výpočtu, vyplývajícím z linearity kvantové evoluce. Předpokládejme, že máme před sebou tabulku čísel, pro něž máme za úkol provést určitou proceduru. Klasicky bychom museli procházet tabulku a výsledky vyčíslovat hodnotu po hodnotě. Kvantová evoluce nám naopak umožňuje provést tuto kalkulaci pro všechny vstupní hodnoty najednou. Připravíme-li totiž na vstup počítače stav, jenž je lineární kombinací stavů kódujících všechny hodnoty z tabulky, a provedeme výpočet, obdržíme stav, který je obdobnou lineární kombinací všech výstupních hodnot! Popsaná vlastnost, tzv. kvantový paralelizmus, nemá obdoby v klasickém světě, jelikož se podstatně opírá o existenci kvantových superpozic.
Ještě však není vyhráno. Jak víme z předchozího, je principiálně nemožné obdržet úplnou informaci o stavu kvantového systému z jednoho měření. Abychom však získali přístup k výsledkům kvantového počítání, musíme nutně nějaké měření provést. Zda se nám podaří dosáhnout radikálního urychlení výpočtu oproti klasickým postupům, tedy nezávisí jen na efektivitě přípravy výstupního stavu počítače, ale též na zvoleném způsobu čtení výsledku. Obecný návod, jak takové čtení provést, neexistuje. Jedním ze základních principů se zdá být maximální využití jevů konstruktivní a destruktivní interference – vzájemné „nakládání“ stavů na sebe v kvantových superpozicích může při běhu výpočetního algoritmu výrazně posílit jedny a zároveň oslabit druhé. Pro optimálně navržený algoritmus lze potom kýžený výsledek odvodit z příspěvků právě těch členů superpozice, které byly interferencí zesíleny. Výpočet je sice nutné několikrát opakovat, počet opakování nutný ke stanovení správného výsledku však není velký (srovnej Shorovu proceduru v rámečku na str. 254).
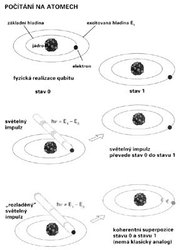
Poté, co jsme si vyložili, jak kvantové počítače pracují a v čem se skrývají výhody i záludnosti jejich použití, se nabízí otázka, proč již velké průmyslové giganty (třeba IBM) nezaplavily svět jejich prvními komerčními exempláři. Důvod je prozaický. Kvantové počítače existují zatím pouze ve stadiu prvních laboratorních pokusů, které vylučují jakékoli praktické použití. Popišme si pro zajímavost jeden z nadějných postupů konstrukce kvantového hradla, o němž se v poslední době diskutuje na stránkách vědeckých časopisů.Jak jsme vysvětlili v předchozích odstavcích, běh kvantového výpočtu se uskutečňuje přirozeným časovým vývojem počítače jakožto fyzikálního systému (mimochodem, proto se někdy o kvantových počítačích mluví jako o analogových přístrojích). Aby bylo možno snadno interpretovat stavy počítače z hlediska kvantové logiky, je nezbytné, aby se počítač skládal z fyzických nosičů jednotek logické informace, tj. qubitů. V jednom z navrhovaných kvantových počítačů jsou nosiči qubitů ionty (uvězněné studené ionty, z angl. cold trapped ions) vázané na lineární mřížce, kterou si lze představit jako řetízek potenciálových jam, v nichž ionty vykonávají kvantové oscilace. Iontům je odebírána energie pomocí laserového ochlazování, čímž se jejich pohyb zpomalí natolik, že relevantní kmitavé stavy jsou pouze stav základní (tzv. nulové oscilace) a první stav excitovaný (přítomnost jednoho kvanta zvukových kmitů – fononu). Aktuální logická informace je zapsána do vnitřních excitačních stavů, přičemž logická kvantová nula odpovídá hladině iontu o nejnižší energii, logická jednička hladině následující (srovnej obr. v předchozím rámečku).
Jak je možno cíleně ovlivňovat časový vývoj stavu série popsaných iontů, a tak například simulovat činnost kvantového hradla? Každý iont je vystaven řízenému působení laserového paprsku, který při přesném nastavení frekvence (energie kvant je rovna rozdílu energií vnitřních stavů) umožňuje díky mechanizmům absorbce a emise měnit logický stav jednotlivých qubitů (tj. řízeně převádět nuly na jedničky apod.). Při určitém rozladění frekvence laseru jsou přechody mezi vnitřními stavy spojeny též se změnami v kmitavých módech systému iontů (interakce pak vlastně mění kvanta světla — fotony v kvanta zvuku — fonony a naopak). Šíření fononu podél řetízku iontů zprostředkovává komunikaci mezi jednotlivými qubity – vhodně načasovaným působením laserů je tak možno měnit vnitřní stav jednoho iontu v závislosti na stavu iontů ostatních. Ukazuje se, že činnost libovolného kvantového hradla lze reprezentovat výše naznačeným způsobem, což činí konstrukci kvantového počítače myslitelnou.
Je tedy jen otázkou času, než se kvantová hradla přenesou z laboratoří do světa komerčního využití? Samozřejmě lze těžko předvídat další vývoj, nicméně faktem zůstává, že na cestě k sestrojení osobního kvantového počítače stále stojí vážné překážky. Kromě technických potíží vynucujících si nejmodernější metody fyziky pevné fáze a nízkých teplot jde i o principiální záležitost, jíž je destruktivní vliv okolního prostředí na hladký průběh kvantového výpočtu.
Problém vměšování se okolních vlivů do výpočtu na počítači je samozřejmě přítomen i na klasické úrovni (kdo někdy hořekoval nad daty smazanými z diskety, kterou si položil na reproduktor, ví, co tím myslíme, řekneme-li, že vnější magnetické pole ovlivňuje nosiče informace), nicméně vzhledem k tomu, že klasickou logickou jedničku dělí od nuly napěťový rozdíl 5V, jsou klasické počítače vůči takovému vměšování poměrně stabilní. Kvantové počítače jsou v tomto ohledu mnohem choulostivější: není-li kvantový systém zcela izolovaný od svého okolí (a to není nikdy), provážou se v kvantových superpozicích navzájem stavy systému a prostředí. Ukazuje se, že toto provázání (angl. entanglement) vede k postupnému a nekontrolovatelnému vychylování výpočetního stavu od stavu předpokládaného při sestavování kvantového algoritmu (zde se spojitá struktura kvantových superpozic projevuje ke škodě věci). V důsledku toho je výsledek výpočtu zatížen chybami narůstajícími s časem exponenciálně a naděje na účelné využití kvantových počítačů se hroutí.
Abychom byli konkrétnější, např. jen pro věrohodné uchování kvantové informace po dobu nezbytnou k faktorizaci tisícimístného čísla (mez výhodnosti kvantového algoritmu před klasickým) by bylo nutné, aby náš počítač pracoval na optických frekvencích (cca 1015 Hz, přičemž takt nejnovějšího mikroprocesoru Pentium je 2.108 Hz). Tato hodnota je a samozřejmě dlouho bude daleko za možnostmi současné techniky, a proto se v poslední době hojně diskutuje o metodě, která by umožňovala účinně se bránit drsnému vměšování prostředí do kvantového výpočtu a oslabit tak meze na takt kvantového počítače. Je zajímavé, že u jejího zrodu stál opět P. Shor, známý již svým řešením faktorizačního problému. S odvoláním na zmíněné pesimistické odhady navrhl zapojit do kvantového výpočtu korekční proceduru, která bude účinně vyvažovat změny vzniklé v důsledku interakce s prostředím. Základem Shorovy metody je využití redundance, tedy uchování logické informace v nadbytečném počtu qubitů. To umožňuje restaurování původní informace, dojde-li k nějakým poruchám. Klasická myšlenka klonování, tj. vytvoření několika identických kopií, však nemohla být přímo použita, neboť linearita kvantové teorie vytvoření kopie daného stavu vylučuje. Kódování redundantních stavů tedy muselo být řešeno rafinovanějším způsobem.
Stejně jako řešení problému rozkladu na prvočísla, tak i tato Shorova práce způsobila zvrat v teorii kvantových počítačů a vyústila v sérii článků, které zpřesňují, zobecňují a kvantifikují původní Shorovu myšlenku. Přestože vývoj v této oblasti ještě není zdaleka u konce, výsledky usilovné činnosti vědců vzbuzují naději, že přinejmenším základní prvky kvantových počítačů již brzy (tedy během několika let) spatří světlo světa.
Literatura
A. Ekert, R. Jozsa: Quantum computation and Shor‘s factoring algorithm, Rev. Mod. Phys. 68, 733–753, 1996C. H. Bennett: Quantum information and computation, Physics Today, March 1995
S. Lloyd: Quantum mechanical computers, Scientific American 273/4, str. 44-50, October 1995
A. Barenco et al.: L´ordinateur sous le charme quantique, La Recherche No. 292, str. 52–57, Novembre 1996
a jako výchozí bod k „brouzdání“ Internetem může posloužit adresa:
eve.phys.ox.ac.uk/QChome.html
Zpět k základům
Schopnost kvantových stavů sdružovat se do libovolných superpozic připomíná geometrické vlastnosti vektorů. V matematické formulaci kvantové teorie je proto fyzikální stav systému reprezentován nějakým vektorem |ψ> abstraktního vektorového prostoru (tzv. Hilbertova prostoru). Každý vektor|ψ> lze vyjádřit jako lineární kombinaci (superpozici) bázových vektorů |φi>,
|ψ> = Σi Αi |φi>
s komplexními koeficienty αi splňujícími podmínku ∑i |αi|2 = 1. Dimenze (počet bázových vektorů) stavového prostoru dané fyzikální soustavy může být různá, třeba 2 nebo také ∞. Například energetické stavy elektronu|nlms) ve vodíkovém atomu (n, l , m a s zde označují po řadě hlavní, vedlejší, magnetické a spinové kvantové číslo) tvoří množinu bázových vektorů ve stavovém prostoru elektronu. Dimenze je v tomto případě nekonečná. Ve fyzikálních situacích však často hraje roli jen určitý omezený počet bázových stavů; efektivní dimenze prostoru stavů je potom konečná.
Jsou-li bázovými stavy |φi> stavy odpovídající jednotlivým (kvantovaným) hodnotám χi veličiny Χ, je pravděpodobnost naměření výsledku χ i ve stavu |ψ> dána výrazem
P|ψ>(χi) = |αi|2
Tak například, pro elektron ve stavu |ψ> = |n=1> – |n=2> bude s pravděpodobností 3/4 naměřena hodnota energie odpovídající hlavnímu kvantovému číslu n = 1 a s pravděpodobností 1/4 hodnota odpovídající n = 2.
Časový vývoj kvantového systému si můžeme představit jako spojitý pohyb stavového vektoru v prostoru stavů, při němž se jednotková délka vektoru zachovává. Důležitou vlastností kvantové evoluce je její linearita: Jestliže se stav |ψ0>za čas t vyvine ve stav |ψt> a stav |χ0) ve stav|χt), pak superpozice α|ψ0> +β|χ0> se vyvine v α|ψt> + β |χt>.
Tyto skutečnosti se v matematické řeči vyjadřují tvrzením, že transformace |ψ0> to |ψt> je unitárním lineárním operátorem.
QUBIT A LOGICKÉ OPERACE
 Klasickými booleovskými stavy se obvykle myslí stavy N klasických bitů, tzn. řady jedniček a nul. Jak jsme již zmínili, kvantová teorie předpokládá i existenci lineárních kombinací těchto stavů. Pro jeden bit tak kromě stavů |1> a |0>, odpovídajícím klasickým logickým hodnotám ANO a NE, musíme uvažovat i libovolné superpozice typu α|0> + β|1>. Přestože si jako logická jednotka bit uchová svou dvouhodnotovou charakteristiku (jeho prostor stavů je stále dvoudimenzionální), nelze už mluvit o klasickém bitu, nýbrž o bitu kvantovém, tzv. qubitu. Ostatně existuje ekvivalentní popis stavů jednoho qubitu jako bodů na (dvourozměrném) povrchu koule. Viz obrázek, kde body na povrchu jsou charakterizovány dvěma úhly ψ a θ, pomocí kterých jsou dány výše uvedené koeficienty α a β, α = eiψ sinθ a β = cosθ.
Klasickými booleovskými stavy se obvykle myslí stavy N klasických bitů, tzn. řady jedniček a nul. Jak jsme již zmínili, kvantová teorie předpokládá i existenci lineárních kombinací těchto stavů. Pro jeden bit tak kromě stavů |1> a |0>, odpovídajícím klasickým logickým hodnotám ANO a NE, musíme uvažovat i libovolné superpozice typu α|0> + β|1>. Přestože si jako logická jednotka bit uchová svou dvouhodnotovou charakteristiku (jeho prostor stavů je stále dvoudimenzionální), nelze už mluvit o klasickém bitu, nýbrž o bitu kvantovém, tzv. qubitu. Ostatně existuje ekvivalentní popis stavů jednoho qubitu jako bodů na (dvourozměrném) povrchu koule. Viz obrázek, kde body na povrchu jsou charakterizovány dvěma úhly ψ a θ, pomocí kterých jsou dány výše uvedené koeficienty α a β, α = eiψ sinθ a β = cosθ.
Obecný stav N-bitového kvantového logického stavu je vektorem 2N-rozměrného prostoru a lze jej vyjádřit formulí
|ψ> = ∑ αn|n>
 kde sčítání probíhá přes všechny klasické booleovské stavy n. Logické operace budou reprezentovány unitárními operátory na příslušném Hilbertově prostoru booleovských stavů. Pro zajímavost si uveďme, jak bude vypadat jednobitové hradlo NOT. Protože má podle své definice převracet nuly na jedničky a naopak, snadno nahlédneme, že je reprezentováno maticí
kde sčítání probíhá přes všechny klasické booleovské stavy n. Logické operace budou reprezentovány unitárními operátory na příslušném Hilbertově prostoru booleovských stavů. Pro zajímavost si uveďme, jak bude vypadat jednobitové hradlo NOT. Protože má podle své definice převracet nuly na jedničky a naopak, snadno nahlédneme, že je reprezentováno maticí
Ta vektor  reprezentující superpozici α|0> + β|1> převede na
reprezentující superpozici α|0> + β|1> převede na  tj. β|0> + α|1>. Dvoubitová hradla budou reprezentována maticemi 4 x 4, tříbitová 8 x 8 atd. Obecně, hradla pracující s N qubity operují mezi 2N-dimenzionálními Hilbertovými prostory, čemuž bude odpovídat i dimenze příslušných operátorů (tj. řád příslušných matic).
tj. β|0> + α|1>. Dvoubitová hradla budou reprezentována maticemi 4 x 4, tříbitová 8 x 8 atd. Obecně, hradla pracující s N qubity operují mezi 2N-dimenzionálními Hilbertovými prostory, čemuž bude odpovídat i dimenze příslušných operátorů (tj. řád příslušných matic).
LASEROVÉ OCHLAZOVÁNÍ
Princip laserového chlazení lze kvalitativně vysvětlit na základě Dopplerova jevu. Uvažme dvouhladinový atom, který vykonává kvantové oscilace v iontové pasti. Oscilační pohyb vede k rozšíření (rozmazání) spektrálních čar. Lze si to představit tak, že v důsledku dopplerovského posuvu kmitá i (jediná) relevantní čára ve spektru. Naladíme-li nyní laser na frekvenci odpovídající pohybu atomu směrem k nám a nasměrujeme-li jeho paprsek proti směru pohybu atomu, dojde (v určitém procentu případů) k absorbci jednoho kvanta energie. Protože toto kvantum nese impulz, jenž je protiležící hybnosti kmitajícího atomu, dojde tak k zbrždění kmitavého pohybu, které se projeví přechodem na nižší oscilační hladinu. Posléze atom vyzařuje energii pohlceného fotonu procesy spontánní emise. Toto vyzařování má však všesměrový charakter, a tedy neovlivňuje módy kmitavého pohybu.
Metodou laserového chlazení lze dosáhnout ultranízkých teplot (např. nedávný teplotní rekord činí několik nanokelvinů), což umožňuje studium chování látek s téměř úplně zamrzlými kmitavými stupni volnosti. Posledním experimentálním úspěchem této techniky byla příprava tzv. Boseho-Einsteinova kondenzátu, jak o tom referoval Vesmír 74, 614, 1995/11, a zcela nedávná realizace tzv. atomového laseru, jak jsme se mohli dočíst i v denním tisku.
FAKTORIZACE
Místo problému faktorizace řešil P. Shor jiný problém klasické vyčíslitelnosti, a to problém hledání periody funkce, jenž je s původním problémem ekvivalentní. Ukažme si, jak se hledá perioda dané funkce na kvantovém počítači.
Předpokládejme, že máme funkci f(x) na diskrétním definičním oboru {0,1, ..., 2N1}. Řekneme, že funkce je periodická s periodou p, kde p dělí 2N, je- li f(x) = f(x + p mod 2N). Funkci f(x) zakódujeme do stavu |ψ >= 2–N/2 ∑ |x,f(x)>, kde se sčítá přes celý definiční obor. Představujeme si zde dva kvantové registry, jeden s N qubity pro registraci proměnné x a druhý pro registraci hodnot f(x) (pro řešení problému faktorizace jde o funkce s danou diskrétní množinou funkčních hodnot.) Vektor |x,f(x)> je pak stavem obou registrů současně a výše uvedený stav |ψ> je rovnoměrnou superpozicí takových stavů. Na stav |ψ> aplikujeme unitární operátor, v němž znalci poznají diskrétní Fourierovu transformaci prvního indexu. Původní stav se tak transformuje
Nyní provedeme měření na prvním registru. Jak jsme již předjímali, takové měření má nutně pravděpodobnostní charakter. Nicméně, pro pravděpodobnost toho, že změříme hodnotu k = a, platí úměra
kde m = 2N/p. Pravá strana je rovna nule kromě případů, kdy a je celočíselným násobkem m. Ze vzájemného rozdílu naměřených hodnot prvního indexu lze dělením snadno vysoudit velikost čísla m. K získání relativně přesného výsledku tedy stačí provést několik málo měření (jak mnoho, závisí samozřejmě na velikostech čísel N a p).
Ke stažení
 Článek ve formátu PDF [311,83 kB]
Článek ve formátu PDF [311,83 kB]




























