Velké umění astronavigace: Od astrolábu po sextant
| 1. 10. 2018Staří mořeplavci prý určovali polohu své lodi podle hvězd. Tato rozšířená romantická představa je ale nesprávná. Metoda astronavigace nikdy nebyla hlavním způsobem, jak navigovat svou loď.
Vyvrácení tohoto mýtu a popisu řízení lodí ve staletích před satelitní navigací se věnuje článek v tištěném říjnovém Vesmíru. Astronavigace a přístroje pro ni používané veřejnost fascinují, podívejme se na obojí trochu detailněji.
První použití astronavigace si vyžádaly plavby přes oceán, pro evropskou mořeplavbu to představuje druhou polovinu patnáctého století. Dva přístroje, tehdy používané k tomuto účelu, byly astroláb a kvadrant. V obou případech šlo o jednoduchá zařízení sloužící k měření úhlové vzdálenosti mezi objektem na obloze (nejčastěji Polárkou nebo Sluncem) a horizontem nebo vertikálním směrem. Těmto úhlům říkáme úhlová výška a zenitová vzdálenost (protože vertikála míří do zenitu, bodu na obloze, který je přímo nad hlavou).
Astroláb a kvadrant
Astroláb je těžký kruh se stupnicí po obvodu, okolo jehož středu se otáčí rameno se dvěma průzory. Přístroj je nahoře opatřen dvěma na sebe kolmými závěsy a váha přístroje zajišťuje, že nula na stupnici míří vždy nahoru. Otáčením ramene tak, aby světlo hvězdy nebo Slunce procházelo oběma průzory naráz, zjistíme jejich úhlovou výšku nebo zenitovou vzdálenost (podle toho, kde má stupnice nulu).
Přístroj zde popsaný bychom měli správně označovat jako námořní astroláb. Kromě něj existuje ještě astroláb astronomický, jehož konstrukce se připisuje starověkému astronomu Hipparchovi. Jde o jakéhosi předchůdce otočné mapy oblohy – kulatá mříž s hroty, kde každý představuje nějakou jasnou hvězdu na obloze, je otočná na pozadí souřadnicové sítě – výšek nad obzorem a azimutů. Po obvodu mříže jsou časové značky a po obvodu desky v pozadí značky datové. Pootočením mříže tak, aby aktuální čas příslušel aktuálnímu datu, bylo možné zjistit výšky a azimuty hvězd. Častější se přístroj používal opačně – změřením výšky zvolené hvězdy (k tomu sloužilo rameno s průzory na jeho zadní straně) a příslušným otočením mříže se pro aktuální datum zjistil místní čas.
Astronomický astroláb má s navigací jen málo společného, protože souřadnicová síť v pozadí funguje pouze pro pevně danou zeměpisnou šířku. Každá jiná šířka by vyžadovala svou vlastní síť a zeměpisná šířka se samozřejmě během plavby průběžně mění. Astronomický astroláb byl přístrojem značně rozšířeným, ale pouze v hvězdárnách na souši.
Kvadrant tvoří obvykle dřevěná čtvrtina kruhu se stupnicí po obvodu a dvěma průzory na jedné z hran. Úhel mezi objektem a horizontem či vertikálou ukazuje šňůrka se závažím, zavěšená ze středu kruhu.
Určení zeměpisné šířky
Úhlová výška objektu je doplněk jeho zenitové vzdálenosti do 90°. Protože jde o triviální přepočet, budeme v další části článku pracovat pouze s úhlovou výškou. Až do závěru 18. století umožňovalo měření úhlové výšky objektů stanovit pouze zeměpisnou šířku. Již od 15. století se k tomuto účelu užívalo buď měření výšky Polárky, nebo polední výšky Slunce.
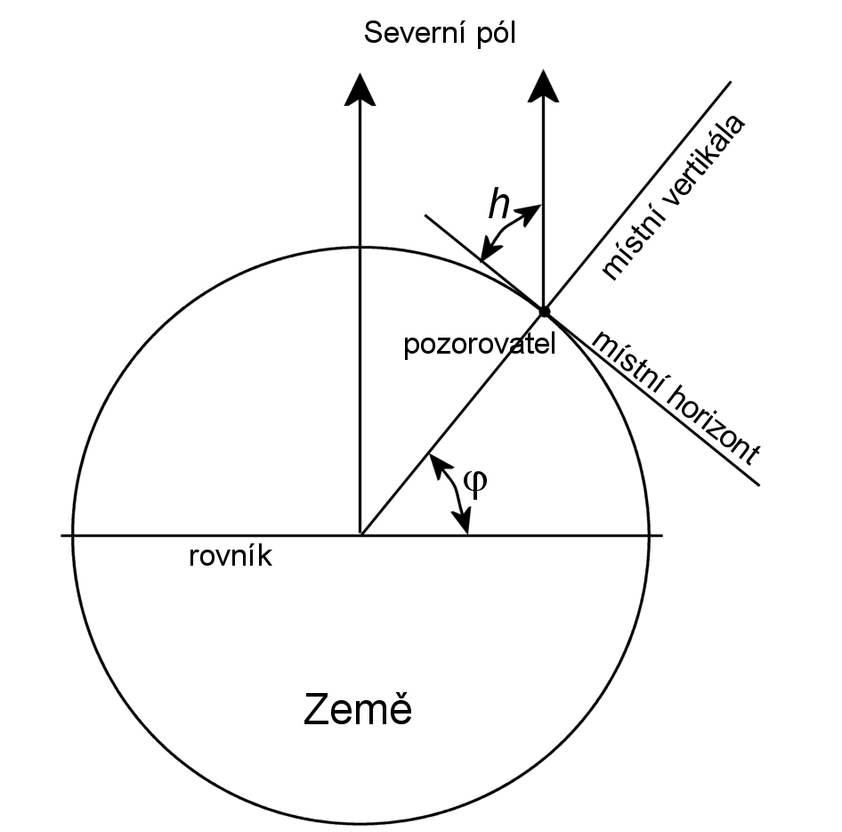
Polárka leží na obloze velice blízko od místa, okolo nějž se zdánlivě otáčí obloha. Toto místo, takzvaný nebeský pól, leží ve směru rotační osy Země. Zeměpisná šířka pozorovatele na povrchu Země je rovna úhlové výšce nebeského pólu nad horizontem, což plyne z obrázku, v němž jsou úhly h (úhlová výška pólu) a j (zeměpisná šířka) totožné.
Změření úhlové výšky pólu a Polárky není ovšem jedno a totéž – Polárka je pouze poblíž pólu. Její úhlová vzdálenost od pólu se navíc v důsledku precese zemské rotační osy mění. V dnešní době je to necelý stupeň, v 15. století to byly stupně tři.
Polárka během „otáčení oblohy“ opisuje okolo vlastního pólu malý kroužek a výšky stejné jako pól dosahuje pouze dvakrát za 24 hodin. Kvadranty používané na moři byly proto často doplněny obrázkem hvězdného okolí Polárky, který ukazoval, jak natočená musí být obloha, aby výška Polárky byla identická s výškou pólu. Případně byla k přístrojům dodávána volvella – otočný disk z tvrdého papíru, který pro okamžité natočení hvězdného okolí udával opravu, kterou bylo třeba ke změřené výšce Polárky přičíst nebo odečíst.
Protože je výška pólu rovna zeměpisné šířce, při plavbě k rovníku klesá severní pól k obzoru a při překročení rovníku na jižní polokouli zmizí za obzorem. Nad jihem se pro změnu vynořuje jižní nebeský pól. Ten má ovšem tu nevýhodu, že poblíž něj se nenachází žádná dostatečně nápadná hvězda.
Oceánské plavby na jižní polokouli tedy přinutily mořeplavce využívat dalšího objektu k určení zeměpisné šířky – Slunce.
Výška Slunce se však v průběhu dne mění, proto je k tomuto účelu použitelná pouze výška maximální – v době kulminace neboli pravého poledne. Jenže polední výška se mění i v průběhu roku. Pokud by Slunce po celý rok stálo přímo nad zemským rovníkem, pak zeměpisná šířka určená z jeho polední výšky bude doplňkem této výšky do 90° (j = 90° – h), což plyne z toho, že směr rovníku je kolmý na směr k pólu (obr. 3). Slunce však nad rovníkem nestojí, jeho zeměpisná šířka, kterou nazýváme deklinace, se mění v průběhu roku od obratníku Raka k obratníku Kozoroha a zpět. O tuto deklinaci musíme výpočet opravit, dostáváme tedy vzorec j = 90° – h + Dec.
Tabulky sluneční deklinace pro každý den v roce sestavovali již antičtí astronomové. V 15. století je stačilo přizpůsobit potřebám mořeplavců.
Jakubova hůl a sluneční kruh
Několik dalších pomůcek pro měření výšek přineslo navigátorům 16. století. Nejznámější z nich je pravděpodobně Jakubova hůl, v jiných jazycích označovaná jako cross-staff nebo ballastella. Její původ sahá opět k antickým astronomům, ale doporučení pro používání na moři se připisuje norimberskému astronomovi Johannovi Wernerovi (1514).
Jde o tyč se stupnicí, po níž se posouvá kolmo upevněná příčka. Konec tyče se přikládá k oku a příčka se posune tak, aby mořský horizont a měřený objekt na obloze byly na jejích koncích. Použití přístroje v praxi pro měření kulminace Slunce popisuje William Bourne v knize A Regiment for the sea z roku 1574.
Aby navigátor neminul okamžik, kdy je Slunce na meridiánu, doporučuje Bourne sledovat jej pomocí kompasu a měření zahájit poté, co je Slunce čárku (cca 11°) na východ od jihu. Jeden konec Jakubovy hole se přiloží do jamky oka, a příčka se posouvá tak, aby její dolní konec byl v jedné linii s horizontem a horní konec se středem Slunce. Toto se provádí tak dlouho, dokud výška Slunce není maximální.
Bourne podotýká, že měřit výšku Slunce pomocí Jakubovy hole je nejlepší, pouze pokud je výška menší než 50°, a to z několika důvodů. Dělení Jakubovy hole je pro menší výšky podrobnější; nad 50° je obtížné sledovat zároveň horizont i Slunce; a ve vyšších výškách je záření Slunce tak intenzivní (píše Bourne), že je obtížné se do něj dívat nechráněným okem. Pro výšky nad 50° doporučuje použít astroláb nebo Mariners’ Ring (viz níže).
Bourne zmiňuje i použití slunečního filtru na Jakubově holi, bohužel k němu neudává žádné další podrobnosti. Píše, že pokud hůl není vybavena filtrem a chceme si chránit oko, použijeme ji tak, že horním koncem příčky zakryjeme celý disk Slunce a pak od měřeného údaje odečteme úhlový poloměr Slunce, který činí 15 úhlových minut (správná hodnota je 16 úhlových minut).
Bourne také popisuje způsob, jakým lze opravit výšku z měření astrolábem, pokud tento nevisí zcela svisle: změříme výšku, otočíme astroláb okolo svislé osy o 180° a změříme ji opět. Zaznamenáme rozdíl obou měření a jeho polovinu odečteme od většího z údajů, nebo přičteme k menšímu (jde o výpočet průměru z obou měření).
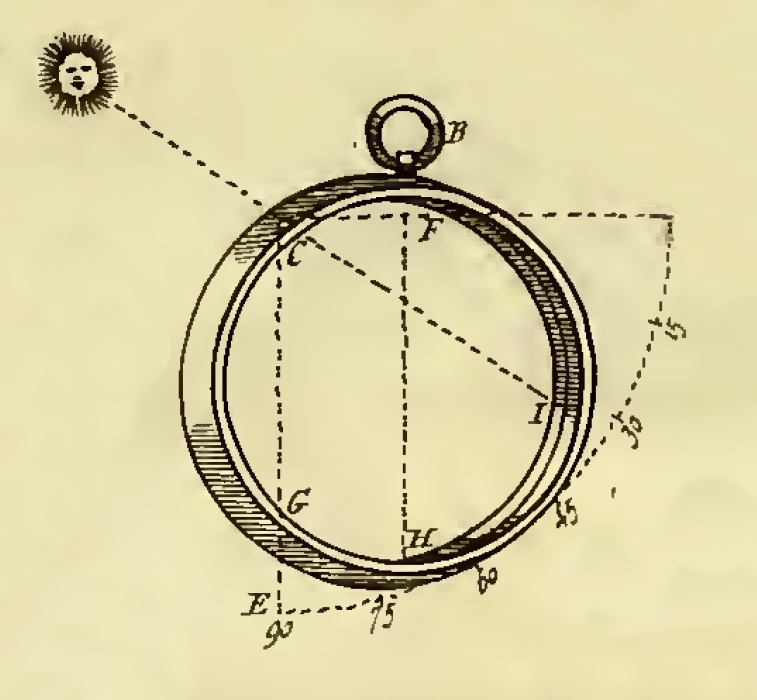
Druhý z přístrojů zmíněný v této části článku se objevuje pod tolika označeními, že bylo obtížné zvolit jeho správný český překlad: Mariners’ Ring, Altitude Ring, Nautical Ring nebo Sun Ring a sloužil výhradně k měření výšky Slunce. Nápad je připisován Pedrovi Nunesovi (De arte adque ratione navigandi, 1573, dnes je známější spíše pod jménem Petrus Nonius), a objevuje se i v pozdějších navigačních manuálech. Jde o svisle zavěšený kruh se stupnicí na vnitřní straně a otvorem ve třech čtvrtinách výšky strany protější. Přístroj se namíří na Slunce otvorem, který se jako světlý bod promítne na stupnici. Kromě dvojnásobné velikosti stupnice oproti astrolábu (při stejné velikosti přístroje) bývají uváděny jeho další výhody – pozorovatel nemusí hledět přímo do Slunce a jasný bod na stupnici se objeví i tehdy, když je Slunce v mírném oparu.
Davisův kvadrant neboli back-staff
Přístroj nesoucí tento název je jeden z mála, u něhož jednoznačně známe autora. Je jím anglický mořeplavec John Davis, který jej poprvé navrhl a popsal v knize Seaman’s secrets (1594). Stal se nejrozšířenějším astronavigačním přístrojem 17. a velké části 18. století. Davis sám jej označuje jako back-staff, protože jde o modifikaci Jakubovy hole (cross-staff).
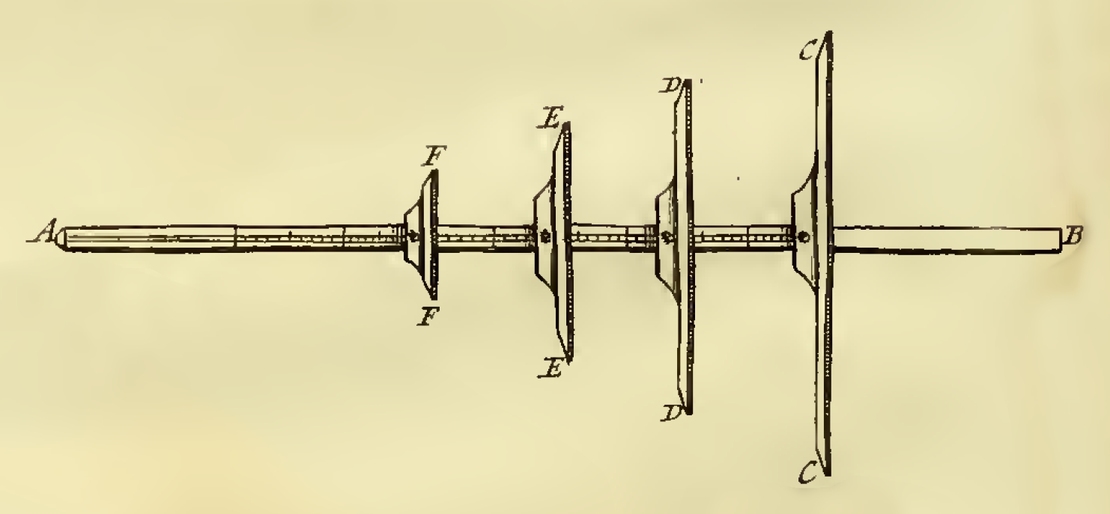
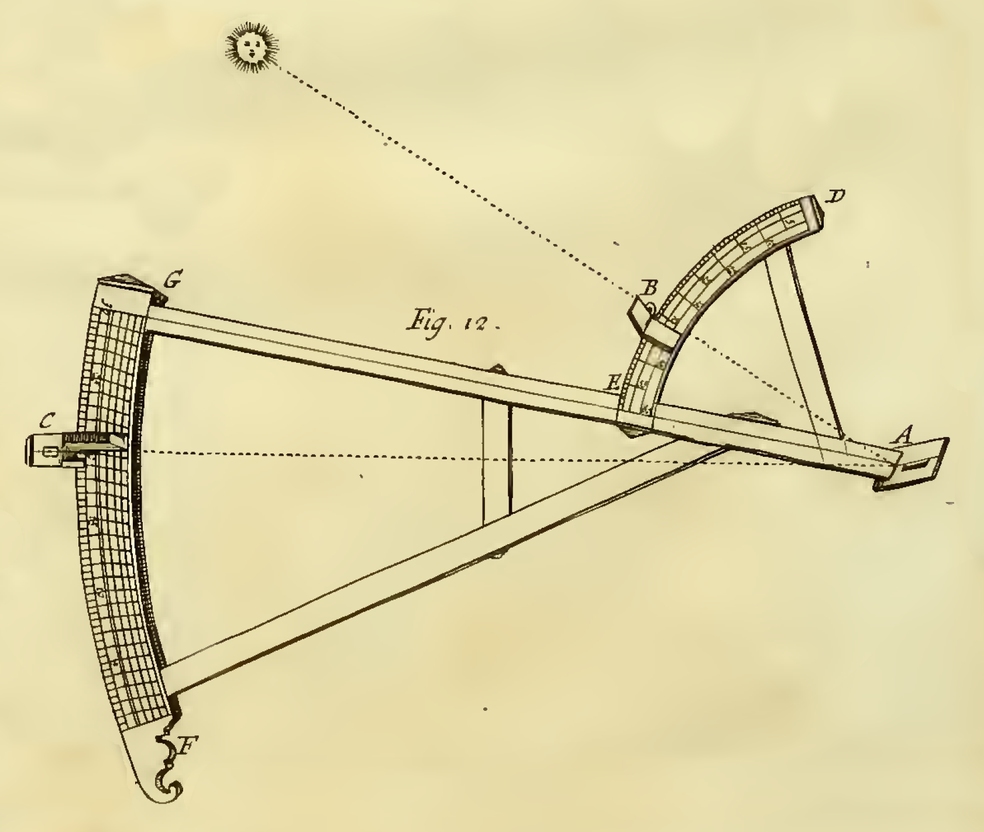
Při popisu konstrukce a použití Davisova kvadrantu se již neobejdeme bez obrázku. Navigátor uchopil přístroj v místě F, okem se díval od ukazatele C přes štěrbinu A na mořský horizont. Ukazatel B se poté nastavil do takové pozice, aby stín jím vržený dopadal na štěrbinu A. Součet úhlů nastavených ukazateli C a B na příslušných stupnicích pak představoval úhlovou výšku Slunce nad horizontem.
Navigátor stál při měření zády ke Slunci, které ho tudíž neoslňovalo. Tato konfigurace dala také přístroji název (back – zadní či pozadu).
Původní Davisův návrh byl ovšem jednodušší – obsahoval pouze jednu stupnici s pohyblivým ukazatelem. Přístroj v dalších staletích prošel nejrůznějšími obměnami; jedné se mu dostalo i od anglického astronoma Edmonda Halleye, jenž navrhl ukazatel B doplnit čočkou, která sluneční paprsky soustředit do ostrého bodu na štěrbině a tím umožní přesnější měření.
Oblibu Davisova kvadrantu mezi mořeplavci dokládá například Andrew Wakely v knize The Mariner’s Compass Rectified z roku 1763, když o něm píše, že je nejrozšířenějším navigačním přístrojem, i když jej již pomalu nahrazuje Hadleyho oktant.
Zrcátkový oktant a sextant
Sextant se stal patrně nejznámějším symbolem astronavigace. Zřejmě zaslouženě, protože umožnil měření výšek objektů nad obzorem do té doby s nebývalou přesností a zůstal v podstatě jediným přístrojem používaným na moři k tomuto účelu dodnes.
Oktant a sextant jsou identické přístroje, které se liší pouze velikostí stupnice a rozsahem měřitelných úhlů. Protože pro většinu aplikací měříme úhlovou výšku, která nemůže přesáhnout 90°, spatřil jako první světlo světa oktant, který umožňuje měřit úhly do této hodnoty (sextant až do 120°).
Princip oktantu vymyslel již Isaac Newton koncem 17. století. Protože jej ale nepublikoval, připisuje se vynález anglickému matematikovi Johnu Hadleymu a americkému optikovi Thomasu Godfreyovi, kteří jej nezávisle na sobě navrhli okolo roku 1730. Oktanty byly původně vybaveny pouze průzorem, až pozdější verze přístrojů začaly být osazovány také dalekohledem, který výrazně zpřesňuje měření.
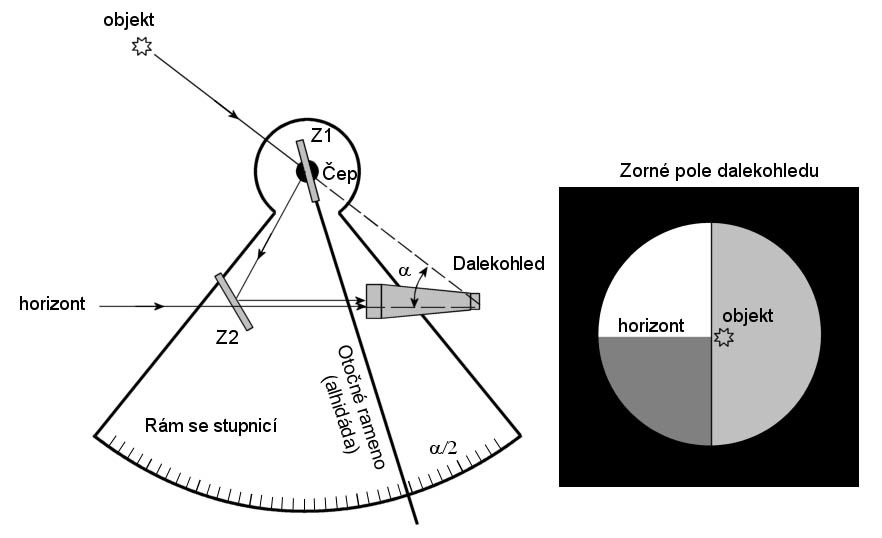
Princip přístroje ukazuje obrázek výše. Základní částí je rám tvořící kruhovou výseč se stupnicí na jeho obvodu. Na rámu je připevněno zrcátko Z2 a dalekohled (případně pouze průzor). Zrcátko Z2 sahá pouze do takové vzdálenosti od rámu, aby zabíralo zhruba polovinu zorného pole dalekohledu. Nahoře je umístěn čep, okolo kterého se otáčí rameno – alhidáda. Spolu s alhidádou se okolo tohoto čepu otáčí i otočné zrcátko Z1.
Paprsek jdoucí od horizontu prochází nalevo od zrcátka Z2 přímo do dalekohledu. Paprsek jdoucí od objektu (např. Slunce nebo hvězdy) se odráží od zrcátka Z1 a poté od zrcátka Z2 a dopadá rovněž do dalekohledu. Při pohledu do dalekohledu sextantu uvidíme zorné pole svisle rozdělené na dvě poloviny. V levé polovině vidíme přímý obraz horizontu, v pravé polovině vidíme odraz oblohy. Sextant ukazuje úhlovou výšku objektu v okamžiku, kdy se podaří otáčením alhidády dostat objekt i horizont v zorném poli do koincidence (na jednu úroveň).
Geometrie odrazu od zrcátek způsobuje, že úhel natočení alhidády (tj. úhel, který svírají vůči sobě roviny zrcátek Z1 a Z2) je roven polovině úhlové vzdálenosti objektu od horizontu. Stupnice přístroje je však konstruována tak, že na ní čteme přímo úhlovou vzdálenost. Vytíná-li tedy rám a stupnice sextantu šestinu kruhu (tj. 60°), lze sextantem měřit úhlové vzdálenosti až do 120°. Stupnice oktantu vytíná pouze osminu kruhu (tj. 45°) a měřit s ním lze úhly do 90°.
Sklon obou zrcátek je možné seřídit pomocí stavěcích šroubků, což kromě vlastností získaných při výrobě činí z oktantu/sextantu velice přesný přístroj. První dřevěné oktanty dosahovaly přesnosti několika úhlových minut, pozdější kovové sextanty až jedné desetiny minuty.
Rozšíření sextantu se překrývá s další novinkou zcela zásadní pro navigaci – námořním chronometrem – hodinami udržujícími přesný čas i za náročných podmínek panujících při plavbě na moři. Chronometr, na němž si navigátoři „vezli“ referenční čas (dnes bychom řekli světový), umožnil porovnáním s místním časem měřit rozdíl zeměpisných délek mezi lodí a referenčním poledníkem. A právě sextant sehrál v tomto nemalou úlohu. Máme-li přesný referenční čas (ukazovaný chronometrem), musíme přesně změřit také místní čas. Nejpřesnějším způsobem určování místního času je jeho přepočet z úhlové výšky Slunce a na její změření potřebujeme přesný přístroj. Chronometr se sextantem umožnily navigátorům stanovit z astronomického pozorování zeměpisnou délku lodi.
Vynález sextantu uzavřel vývoj astronavigačních přístrojů. I když také prošel řadou vylepšení, principiálně nic nového již vymyšleno nebylo. A vzhledem k tomu, že astronavigaci prakticky nahradila satelitní navigace, nedá se ani očekávat, že by se v budoucnu na tomto tvrzení něco změnilo.
Metoda Intercept
Než však uzavřeme tento článek, popišme si ještě jednu astronavigační metodu, objevenou v druhé polovině 19. století, která umožnila stanovit z několika měření současně zeměpisnou šířku i délku lodi. Tato metoda se v astronavigaci stala nejrozšířenějším způsobem určování polohy.
Nejdřív si musíme definovat důležitý pojem – substelární bod (v případě Slunce jej označujeme jako bod subsolární, v případě Měsíce jako sublunární). Je to místo na povrchu Země, které se nachází přímo pod objektem (hvězdou). Pokud bychom se v tomto místě nacházeli, uvidíme daný objekt přímo nad hlavou. Zeměpisné souřadnice tohoto bodu pro libovolné datum a čas v daném roce tvoří hlavní náplň každoročně vydávané publikace zvané Námořní almanach.
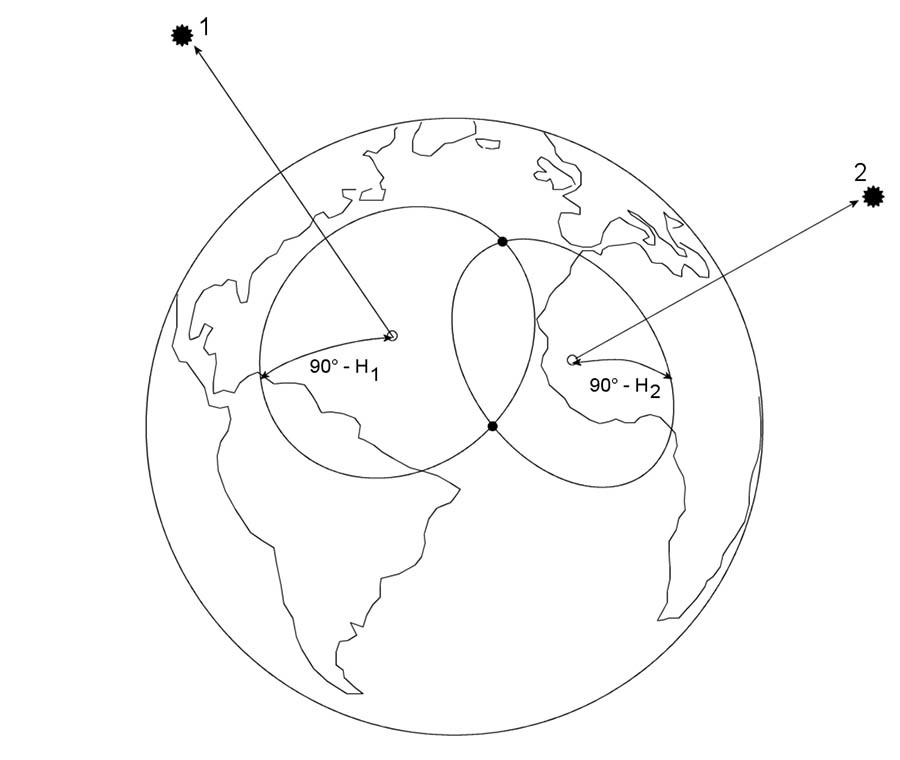
Pro metodu Interceptu měříme vždy výšky minimálně dvou objektů nad horizontem. Začněme prvním z objektů, pro který jsme v čase T1 naměřili výšku nad obzorem h1. Pro čas T1 nalezneme v almanachu zeměpisné souřadnice substelárního bodu objektu. Protože substelární bod leží na povrchu Země přímo pod objektem, pokud bychom se nacházeli v tomto bodě, objekt by byl nad naší hlavou.
Jeho výška nad obzorem by tedy byla 90°. My jsme však změřili výšku jinou: h1. Naše úhlová vzdálenost od substelárního bodu na povrchu Země je tedy 90° – h1. Všechna místa na povrchu Země s touto vzdáleností leží na kružnici se středem v substelárním bodě. Tuto kružnici nazýváme poziční kružnicí a někde na ní je naše poloha. Obdobně provedeme měření výšky h2 pro druhý objekt. Získáme tak druhou poziční kružnici se středem v substelárním bodě druhého objektu a poloměrem 90° – h2. Naše poloha je pak na průsečíku těchto dvou kružnic.
Podle metody Intercept se však v praxi nepostupuje, a to z několika důvodů:
1. Poziční kružnice bychom mohli kreslit na zemském glóbu, ale ten má tak malé měřítko, že výsledný průsečík bychom získali pouze s velmi malou přesností.
2. Na mapě kreslit poziční kružnice nelze, protože mapové zobrazení nezachovává délky a kružnice se na mapě zobrazí jako složitější křivky. Navíc poloměry kružnic jsou obrovské a jejich středy budou většinou ležet mimo mapu, takže by ani nebylo kam „zapíchnout kružítko“.
Tyto nesnáze se řeší tak, že namísto pozičních kružnic se do mapy kreslí jejich tečny – poziční přímky. Vzhledem k velkým poloměrům je nahrazení kružnic jejich tečnami velmi dobrou aproximací. Tečny se konstruují poblíž průsečíku obou kružnic, který ale dopředu neznáme, proto je základním předpokladem pro metodu Intercept alespoň přibližná znalost naší polohy. Podrobný popis nalezení pozičních linií, které se řeší pomocí vzorců ze sférické trigonometrie (buď výpočtem, nebo pomocí tabulek), už je nad rámec článku.
Zájemci o hlubší porozumění astronavigace a její praktické použití na moři mohou navštívit kurzy, které autor článku pořádá v Praze, viz http://www.marine4u.cz/Kurzy-a-skoleni, nebo pro bližší informace kontaktujte autora pomocí emailu: petr.scheirich@gmail.com.
O autorovi
Petr Scheirich