Symetrie ve výpočetní složitosti

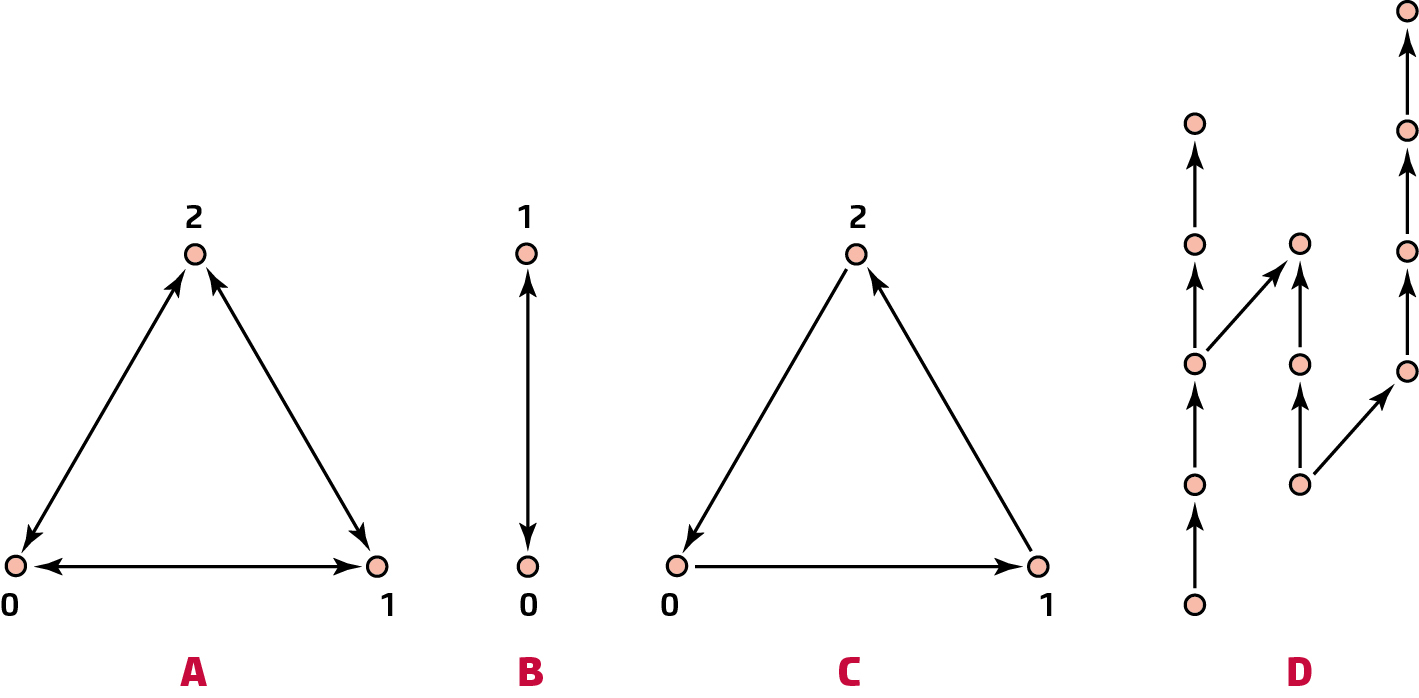
Který z objektů na obrázku 1 je nejméně symetrický? Jak rychle lze rozdělit nějaké množství lidí do tří skupin tak, aby žádní dva nepřátelé nebyli ve stejné skupině? A jak to spolu souvisí?

Odpověď na první otázku se zdá být jasná. Obrázek 1A se nezmění, jakkoliv proházíme puntíky 0, 1 a 2, symetričtější už být ani nemůže. Stejně tak obrázek 1B je tak symetrický, jak jen může být. Na druhou stranu obrázek 1D je zcela asymetrický – cokoliv s puntíky uděláme, obrázek se změní. Obrázek 1C je někde mezi těmito dvěma extrémy: cyklické prohození všech puntíků (0 → 1 → 2 → 0 nebo 0 → 2 → 1 → 0) obrázek zachová, kdežto například prohození puntíků 0 a 1 obrázek nezachová, změní se totiž orientace šipek. Odpověď na otázku je tedy zřejmě 1D.

Na otázku se ale dá, jak uvidíme, správně odpovědět i jinak: nejméně symetrický je objekt na obrázku 1A!

Symetrie

Objekty na obrázku 1 znázorňují tzv. grafy. Graf tvoří množina vrcholů a množina hran, přičemž hranou se myslí uspořádaná dvojice vrcholů.¹⁾ Na obrázku 1 jsou vrcholy nakresleny jako puntíky a hrany jako šipky. Například graf na obrázku 1A má množinu vrcholů {0,1,2} a množinu hran {01,10,02,20,12,21}; graf na obrázku 1C má množinu vrcholů {0,1,2} a množinu hran {01,12,20}. Příkladem grafu „ze života“ je graf, jehož vrcholy jsou lidé, přičemž AB je hrana, pokud člověk A má rád člověka B. Obecnější pojem „hypergraf“ se definuje podobně, ale hrany jsou uspořádané „vícetice“ (trojice, čtveřice, …) vrcholů.

Intuitivní představu symetrie grafu dobře zachycuje pojem automorfismu. Automorfismem nějakého grafu se rozumí zobrazení f přiřazující každému vrcholu x nějaký vrchol f (x), které je vzájemně jednoznačné a zachovává hrany. Vzájemná jednoznačnost znamená, že každý vrchol y má právě jeden vzor, tj. vrchol x takový, že f (x) = y. Zachovávání hran znamená, že je-li xy hrana, pak f (x)f (y) je také hrana. Příkladem automorfismu grafu na obrázku 1C je zobrazení f definované předpisem f (0) = 1, f (1) = 2, f (2) = 0 (tj. cyklické prohození vrcholů zmíněné výše). Skutečně f je vzájemně jednoznačné, protože např. 0 má jediný vzor, a to 2, ap. Zachovává také hrany, protože f (0)f (1) = 12, f (1)f (2) = 20 i f (2)f (0) = 01 jsou hrany.

Grafy (a mnohé jiné druhy objektů) tak můžeme porovnávat podle symetričnosti: graf H můžeme považovat za alespoň tak symetrický jako graf G, pokud každý automorfismus grafu G je také automorfismem grafu H. Takové porovnání objektů podle jejich symetrií je užitečné v mnohých, velmi různorodých partiích matematiky. Konkrétnější příklad: čtenář možná slyšel o tom, že neexistuje vzoreček na řešení algebraických rovnic 5. stupně. Důvodem je, velmi zhruba, že některé rovnice 5. stupně mají příliš složitou množinu symetrií.

Pojem polymorfismu zobecňuje pojem automorfismu dvěma směry: vzdáme se požadavku vzájemné jednoznačnosti a – což je podstatnější – povolíme zobrazení f více proměnných. Přesněji polymorfismus r proměnných grafu G je zobrazení přiřazující každé r-tici (ne nutně různých) vrcholů x₁x₂ …x_r vrchol f (x₁x₂ …x_r), přičemž zachovává hrany, tzn. jsou-li x₁y₁, x₂y₂, …x_ry_r hrany, pak f (x₁x₂ …x_r)f ( y₁y₂ …y_r) je také hrana. Příkladem zajímavého polymorfismu tří proměnných grafu na obrázku 1B je zobrazení, které trojici x₁x₂x₃ přiřadí nejpopulárnější hodnotu mezi x₁, x₂, x₃, tedy f (000) = 0, f (100) = 0, f (101) = 1 ap. Zobrazení f skutečně zachovává hrany, stačí ověřit podmínku pro všech 2 × 2 × 2 = 8 trojic hran, např. 01,01,10 jsou hrany a skutečně platí, že f (001)f (110) = 01 je také hrana (zvládnete ověřit podmínku lépe?). „Nezajímavým“ příkladem polymorfismu jedné proměnné je jakýkoliv automorfismus. Pro graf na obrázku 1B jde o zobrazení definované předpisem f (x) = x a zobrazení definované předpisem f (x) = 1 – x. Existují také polymorfismy, které mají více proměnných (r > 1), ale jsou to jen zamaskované automorfismy (např. f (x₁x₂ …x₁₇) = 1 – x₂ pro tentýž graf), a rovněž je považujeme za nezajímavé. Graf na obrázku 1B má i zajímavé polymorfismy, jak jsme viděli na prvním příkladu. Zajímavé polymorfismy mají i grafy na obrázku 1C a 1D (najdete nějaké?). Na druhou stranu, graf na obrázku 1A žádné zajímavé polymorfismy nemá (zkuste ověřit, není to úplně snadné).

Automorfismy jsou, alespoň pro malé struktury, vidět z obrázku téměř na první pohled. Na druhou stranu polymorfismy většinou vidět nejsou ani pro malé struktury, a to ani na pohled druhý nebo třetí. Můžeme na ně nahlížet jako na složitější, skrytější či hlubší symetrie.²⁾

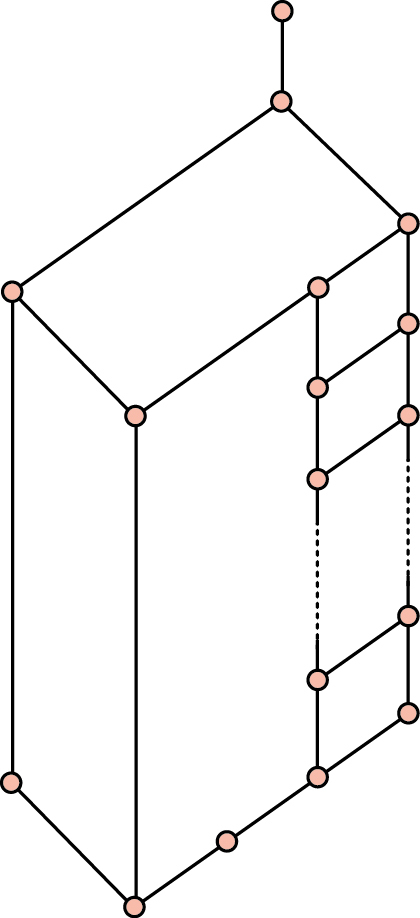
O tom, nakolik jsou polymorfismy složitější než automorfismy, si lze vytvořit představu porovnáním hypergrafů s malým množstvím vrcholů podle polymorfismů. Pro případ dvou vrcholů je výsledek (který vyplývá z prací E. Posta a dalších) znázorněný na obrázku 2. Případ tří vrcholů ještě nikdo nevyřešil a možná ani nevyřeší. Na druhou stranu, pokud použijeme porovnání podle automorfismů, pak obdobné obrázky pro malé počty vrcholů (jako dva a tři) lze vytvořit snadno.

Polymorfismy jsou tedy složitější symetrie. Jsou také k něčemu dobré? Uvidíme, že ano, pojďme se ale nejprve podívat na druhou otázku z úvodu.

Hypergrafy podle polymorfismů. Čáry z nějakého hypergrafu k jinému, který leží výše, značí, že každý polymorfismus prvně zmíněného hypergrafu je polymorfismem onoho výše položeného. Stejně symetrické hypergrafy nejsou na obrázku rozlišeny.

Výpočetní složitost

Výpočetní problém je úloha pro počítač: máme specifikovány povolené vstupy a pro každý vstup očekávaný výstup. Příkladem jednoduchého výpočetního problému je násobení čísel, kdy na vstupu očekáváme dvě čísla (řekněme přirozená) a výstupem má být jejich součin. Dalším příkladem je výpočetní problém, jehož vstupem je soustava lineárních rovnic (řekněme s racionálními koeficienty) a výstupem nějaké její řešení, případně sdělení, že soustava řešení nemá. Ještě jiným příkladem je problém z úvodu článku, kdy vstupem je seznam lidí spolu s informacemi, kdo je koho nepřítel, a výstupem má být rozdělení do tří skupin tak, aby žádní nepřátelé nebyli ve stejné skupině (případně sdělení, že takové rozdělení neexistuje). Tento problém budeme nazývat „problém 3 skupin“,³⁾ podobně budeme mluvit o problému 2 skupin, 4 skupin atd.

Výpočetní složitost je obor na pomezí matematiky a informatiky, který zkoumá, jak efektivně lze nebo nelze výpočetní problémy řešit. Jedním z důležitých měřítek složitosti výpočetního problému je jeho tzv. časová složitost, kde nám jde zhruba o to, kolik nejvýše kroků výpočtu, v závislosti na délce vstupu, potřebuje „nejlepší“ korektní algoritmus.

Podívejme se nejprve na problém násobení čísel. Délka vstupu n je zde přibližně rovna celkovému počtu číslic vstupních čísel. Jedním z korektních algoritmů je školské násobení „pod sebe“, které potřebuje řádově n² kroků (přesný počet závisí na tom, co přesně rozumíme krokem ap.). Časová složitost násobení je tedy nejvýše n². Pro zajímavost uveďme, že ve skutečnosti je složitost nižší, jsou známy algoritmy, kterým stačí pro velká n kroků daleko méně.

Pro problém řešení soustav lineárních rovnic známe například eliminační algoritmus, který ukazuje, že složitost tohoto problému je nejvýše n³ (a opět je ve skutečnosti nižší). Pro problém 2 skupin existuje algoritmus, který vyžaduje řádově n kroků (najdete ho?). Obecně problémy, které lze vyřešit v nejvýše nk krocích pro nějakou konstantu k, považujeme za efektivně řešitelné.

Pro problém 3 skupin je situace horší. Naivní algoritmus, který postupně vyzkouší všechny možnosti rozdělení do skupin a pro každou možnost zkontroluje podmínku na nepřátele, je zoufale pomalý, potřebuje v nejhorším případě řádově 3ⁿ kroků. Číslo 3ⁿ je pro velká n daleko větší než n³, je dokonce daleko větší než nk pro jakoukoliv konstantu k. Je možná překvapivé, že žádný podstatně rychlejší algoritmus na tento problém neznáme. Ve skutečnosti otázka, zda jde problém 3 skupin efektivně řešit, je jedním ze sedmi matematických tzv. problémů tisíciletí. Za vyřešení každého z těchto sedmi hlavolamů vypsal v roce 2000 Clayův matematický institut odměnu milionu dolarů. Odpověď na druhou otázku z úvodu článku je tedy jednoduchá: „Nevíme.“ Většina informatiků by si spíše vsadila na zápornou odpověď.

Výpočetní problémy si můžeme uspořádat tak, že problém P prohlásíme za nejvýše tak těžký jako problém Q, značíme P ≤ Q, pokud lze problém P převést na problém Q v nejvýše nk krocích, pro nějakou konstantu k. Problémy P a Q prohlásíme za stejně těžké, pokud platí, že P je nejvýše tak těžký jako Q a současně Q je nejvýše tak těžký jako P (tedy P ≤ Q a Q ≤ P). Jedním z cílů teoretické informatiky je poznat, kde který výpočetní problém v tomto uspořádání leží. Viděli jsme, že násobení, soustavy lineárních rovnic a problémy 2 skupin jsou stejně těžké výpočetní problémy, totiž nejlehčí – efektivně řešitelné. Zda je problém 3 skupin také efektivně řešitelný, nevíme, ale lze ukázat, že je stejně těžký jako problém k skupin pro jakékoliv k ≥ 3 (zkuste to!).

Hypergrafy podle zjednodušených polymorfismů.

Problémy splnitelnosti omezujících podmínek

Problém 3 skupin lze také přeformulovat následujícím způsobem. Vstup tvoří proměnné x₁, …x_m (jedna proměnná v této formulaci odpovídá jednomu člověku v původní formulaci) spolu s omezujícími podmínkami, které požadují, aby některé dvojice proměnných (odpovídající nepřátelům v původní formulaci) byly hrany grafu na obrázku 1A. Očekávaným výstupem je přiřazení hodnot 0, 1, nebo 2 všem proměnným (odpovídající tomu, do jaké skupiny koho zařadit), aby všechny omezující podmínky byly splněny.⁴⁾ V tomto smyslu je problém 3 skupin totéž jako problém splnitelnosti omezujících podmínek (zkráceně CSP z anglického Constraint Satisfaction Problem) určený grafem na obrázku 1A. Podobně bychom definovali CSP určený jakýmkoliv jiným grafem (nebo obecněji hypergrafem). Pro každý (hyper)graf tak dostáváme jeden výpočetní problém a celkově máme nekonečnou třídu výpočetních problémů. Tato třída je zajímavá z mnoha důvodů, například proto, že obsahuje důležité výpočetní problémy: kromě problémů k skupin jsou to různé varianty splnitelnosti výrokových formulí nebo řešení soustav rovnic nad konečnými obory (ale např. problém násobení čísel ani problém řešení soustav rovnic nad racionálními čísly takto formulovat nelze).

Průlom ve studiu složitosti CSP se podařil koncem 20. století. A. Bulatov, P. Jeavons, A. Krokhin a další zjistili, že složitost CSP určeného nějakým grafem závisí pouze na polymorfismech daného grafu:

Pokud je graf H aspoň tak symetrický jako graf G (ve smyslu polymorfismů), pak CSP určený grafem H je nejvýše tak těžký jako CSP určený grafem G. Po tomto průlomu následoval rychlý rozvoj oboru, který vyvrcholil v roce 2017, kdy A. Bulatov a D. Zhuk dokázali tzv. dichotomii: CSP určený grafem G je buď efektivně řešitelný (a to v případě, že G má dostatečně zajímavé polymorfismy), nebo stejně těžký jako problém 3 skupin (v opačném případě). Tento výsledek nám dává téměř úplnou informaci o pozici CSP při uspořádání diskutovaném výše, zbývá „jen“ vyřešit zmíněný milionový problém.

Co dál

Viděli jsme, že pro jistou, dost velkou třídu výpočetních problémů je složitost určena symetriemi: čím je problém symetričtější, tím je lehčí. Je ale potřeba místo klasických symetrií (automorfismy) používat liberálnější definici symetrií (polymorfismy).

Jedním z aktivních směrů výzkumu je snaha rozšířit tento poznatek na širší třídy výpočetních problémů a použít jej pro klasifikaci složitosti, tak jak se to podařilo pro CSP. Takovou širší třídou jsou například tzv. CSP s příslibem.

Příkladem je problém rozdělení lidí do k skupin (kde k ≥ 3 je nějaké pevně zvolené číslo), máme-li slíbeno, že rozdělení do 3 skupin je pro daný vstup možné. Pro k = 3 jde v podstatě o problém 3 skupin. Docela nedávno se podařilo ukázat, že volba k = 4, dokonce ani k = 5 problém nezlehčí. Už pro k = 6 ale časovou složitost neznáme. Je tento problém stále stejně těžký?

Souvisejícím směrem výzkumu je snaha symetrie zjednodušit, ale tak, aby stále zachycovaly časovou složitost. Příkladem nedávného pokroku je zjednodušení obrázku 2 do podoby na obrázku 3.

Dlouhodobou vizí je rozšířit platnost hesla „čím symetričtější, tím lehčí“ na všechny výpočetní problémy, a dát tím uspokojivou a krásnou odpověď na fundamentální otázku teoretické informatiky: Co způsobuje, že je výpočetní problém lehký, nebo těžký?