Molekulární krystaly v počítači

O kvantové mechanice se často mluví s nádechem mystiky a s důrazem na paradoxy, příkladem budiž neživá-nemrtvá Schrödingerova kočka. Podobné příklady ale často zastiňují skutečný význam kvantové mechaniky. Schrödingerova rovnice nebo její relativistické zobecnění, Diracova rovnice, nám totiž nabízejí způsob, jak vysvětlit atomární strukturu látek a získat jejich další vlastnosti (barvu, pružnost atd.). Není tedy divu, že kvantová mechanika je využívána nejen pro pochopení nebo ověření experimentálních dat, ale také pro předpovědi vlastností ještě neexistujících materiálů.

Pro studium látek na atomární úrovni je často postačující tzv. nečasová Schrödingerova rovnice, HΨ = EΨ, ve které navíc uvažujeme, že polohy atomových jader jsou fixované a kvantově se chovají jen elektrony. Hamiltonián H popisuje fyzikální vazby mezi částicemi v systému a jejich pohybovou energii. Řešením získáme energii E a vlnovou funkci Ψ. Energie nám udává stabilitu daného systému, přičemž s klesající energií stabilita roste. Energii tak můžeme využít pro nalezení optimální struktury systému. Uvažujeme-li například systém se dvěma vodíky a jedním kyslíkem, můžeme jádra umisťovat různě v prostoru a pro každou konfiguraci vypočítat energii ze Schrödingerovy rovnice. Nejnižší energii potom nalezneme pro strukturu molekuly vody.

Z vlnové funkce Ψ můžeme získat elektronovou hustotu, tedy pravděpodobnost výskytu elektronů. Ta nám konkrétně pro molekulu vody ukáže, že elektrony se částečně od vodíků přesunou ke kyslíku. Celkově potom okolí vodíku vykazuje kladný náboj, okolí kyslíku náboj záporný. Molekula má tedy dipólový moment a je polární.

V klastrové expanzi vytvoříme z celého systému všechny možné dvojice, trojice atd. molekul a vazebnou energii celého systému vypočteme z vazebných energií těchto malých částí.

Ze Schrödingerovy rovnice můžeme také získat informaci o tom, jak spolu budou interagovat dvě nebo více molekul. Tedy zda se budou „přitahovat“, nebo „odpuzovat“. Pokud budeme uvažovat různé vzájemné polohy dvou molekul a vypočteme pro každou polohu energii ze Schrödingerovy rovnice, získáme opět informaci o tom, které konfigurace jsou pro molekuly energeticky více a které méně výhodné. Ty první budou mít energii nižší, druhé vyšší. Změnu energie po seskupení molekul nazýváme vazebnou energií. Například pro dvě molekuly vody je výhodné takové vzájemné uskupení, ve kterém je vodík jedné z molekul nasměrován na kyslík druhé molekuly. Tomuto uspořádání říkáme vodíkový můstek.

Struktura dimeru kyseliny dinitrobenzoové (vlevo) a kyseliny nikotinové (vpravo) vyňatá z jejich kokrystalu. V něm dochází k přesunu jádra vodíku mezi molekulami, které tak získají záporný a kladný náboj.

Kvantová mechanika prakticky

Ačkoliv nám kvantová mechanika nabízí úžasné možnosti pro pochopení světa na úrovni atomů, její použití naráží na několik problémů. Přesné analytické řešení Schrödingerovy rovnice je možné jen pro velmi jednoduché systémy. Nejsložitější z nich je molekula H₂⁺, tedy molekula obsahující jeden elektron. Jakmile je v systému více elektronů, je možné nalézt jen přibližné řešení. Důvodem je vzájemné odpuzování elektronů, které rovnici komplikuje. Zjednodušeně řečeno, elektrony se v systému nepohybují nezávisle, ale chování každého je navzájem provázané (korelované) s chováním ostatních elektronů. Důsledkem je potom velmi složitá vlnová funkce.

Jeden z možných způsobů přibližného řešení Schrödingerovy rovnice spočívá vtom, že se provázanosti zbavíme a místo jedné vlnové funkce pro mnoho elektronů hledáme sadu funkcí, každou pro jeden elektron. Těmto funkcím říkáme orbitaly a této aproximaci jednoelektronová. Elektrony v orbitalech potom v nejjednodušším případě interagují pouze s celkovou elektronovou hustotou a vzhledem k nerozlišitelnosti elektronů si mohou navzájem orbitaly vyměnit. Toto přiblížení nazýváme Hartreeho-Fockova metoda. Započtením efektů provázaného pohybu elektronů (korelace) je možné na základě zjednodušeného řešení získat přesnější energii. Tyto výpočty jsou často o několik řádů výpočetně náročnější než zjednodušené řešení, ale jsou nutné, pokud chceme získat velmi přesnou hodnotu energie nebo jiných vlastností.

Na jednočásticové aproximaci jsou také založeny metody vycházející z teorie funkcionálu hustoty (anglicky density functional theory, DFT). V nich jsou efekty korelace a výměny elektronů přibližně popsány členy v hamiltoniánu. Tento přístup je velmi efektivní a výpočty využívající DFT jsou velmi rozšířené. Jelikož jsou ale efekty korelace a výměny popsány přibližně, v některých případech nemusí být přesnost dostatečná. Například u elektronových korelací na větší vzdálenosti, důležitých například pro vazby mezi atomy nebo molekulami.

Pro použití na reálné systémy musíme Schrödingerovu rovnici zjednodušit. Kromě toho ji ale také musíme „přeložit“ počítači. I v jednoelektronové aproximaci jsou totiž orbitaly dány jako funkce a rovnice pro ně obsahují derivace a integrály, což není formulace vhodná pro počítače. Elegantní (a přibližné) řešení tohoto problému spočívá v tom, že použijeme sadu vhodných funkcí, říkáme jim bázové, a orbitaly hledáme jako kombinace těchto funkcí. Jejich použitím získáme rovnice, které může počítač vyřešit. V současnosti existuje řada počítačových programů, které řeší rovnice kvantové mechaniky pro atomární a molekulové systémy. Pro zajímavost dodejme, že použití těchto programů často zabírá největší podíl výpočetního času na superpočítačích.

V jednočásticové aproximaci se elektrony pohybují ve vystředovaném (zprůměrovaném) potenciálu ostatních elektronů (tzv. střední pole - mean field, A). Pro získání přesnějších energií je třeba započítat korelace mezi elektrony, například po párech (B), nebo (pro vyšší přesnost) zahrnující všechny elektrony (C).

Molekulární krystaly

Počítačové simulace jsou často využívány pro studium molekulárních krystalů. Jedná se například o vodní nebo suchý led a také o krystaly léčiv.

Jaké vlastnosti molekulárních krystalů nás mohou z hlediska výpočtů zajímat? Základním problémem je struktura systému, tedy jak jsou molekuly vůči sobě navzájem uspořádané. Další vlastnosti souvisejí s dynamikou systému, tedy jak se atomy a molekuly v krystalu pohybují – vibrují. Tyto pohyby, tedy hlavně frekvence vibrací, je totiž možné měřit experimentálně, a lze tedy výsledky výpočtu a experimentu porovnat. Podobně je možné vypočítat a porovnat další experimentálně měřitelné veličiny, jako jsou optická spektra (excitace elektronů) nebo spektra nukleární magnetické rezonance.

Jedním z problémů studovaných v naší skupině je výpočet vazebné energie molekulárních krystalů, což je energie uvolněná vytvořením krystalu ze samostatných molekul. Tyto výpočty jsou relativně snadné pomocí metod DFT, ale jejich přesnost nemusí být dostatečná. Pro velmi přesné metody je zase výpočet kvůli jejich výpočetní náročnosti složitý nebo nemožný. Zabýváme se využitím a testováním metod, které jsou výpočetní náročností i přesností mezi DFT a vysoce přesnými metodami.

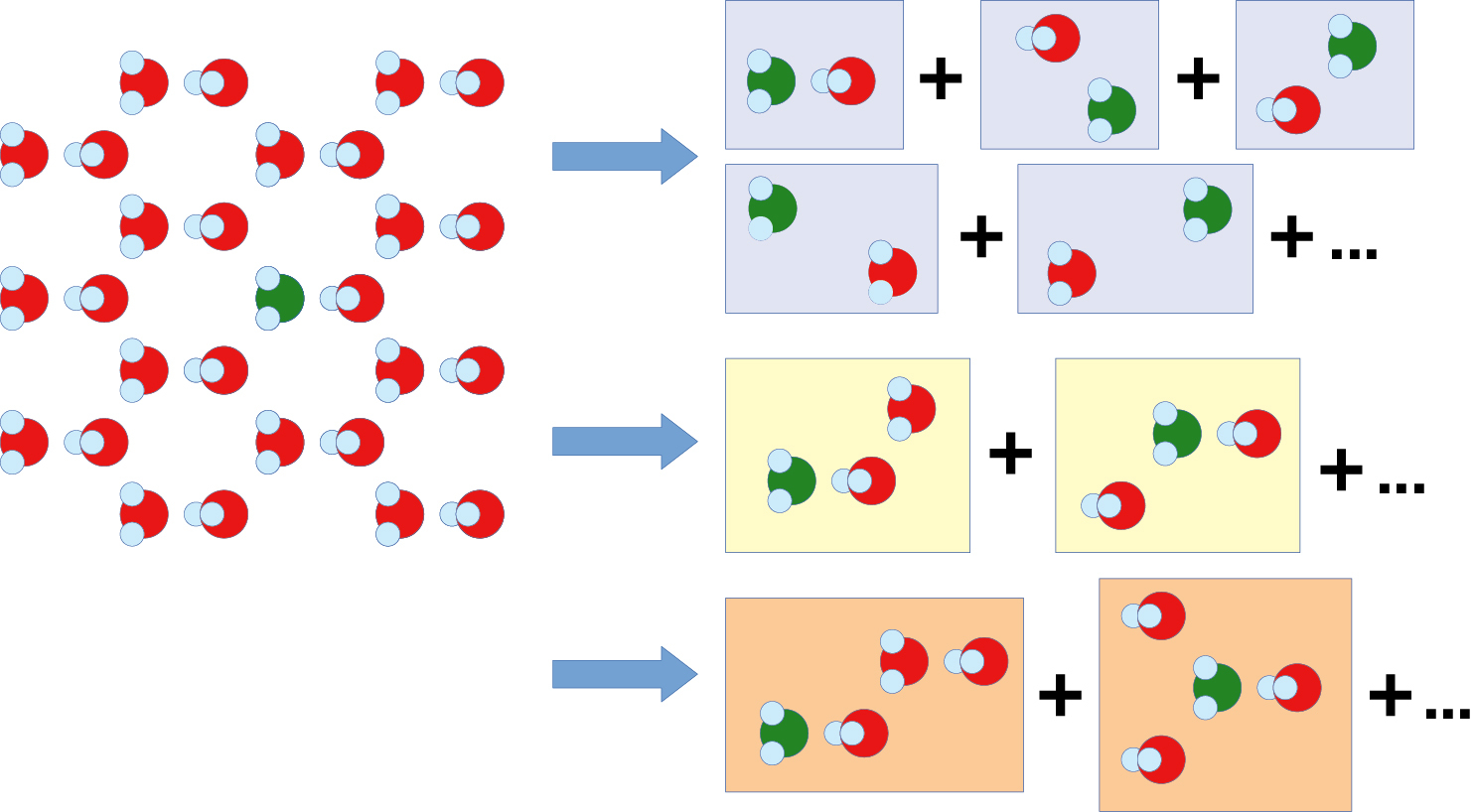
Pro velmi přesné metody lze vazebné energie krystalů vypočítat pomocí tzv. klastrové expanze (obr. 1). Krystal si rozdělíme do dvojic, trojic atd., vypočteme vazebné energie těchto částí a celkovou vazebnou energii z nich poskládáme. V tomto přístupu je ale problém určit, kolik jednotlivých dvojic nebo trojic je potřeba započítat, a které už můžeme zanedbat, neboť jejich příspěvek je mizivý. Této otázce jsme se věnovali v naší loňské publikaci, ve které jsme pro jednodušší metodu zahrnující korelace porovnávali výsledky přímého výpočtu vazebné energie a její klastrové expanze [1]. Ačkoliv jsme ukázali, že shodné výsledky lze získat, také jsme narazili na několik nečekaných problémů. Například přesnost některých výpočtů se s rostoucím počtem bázových funkcí nezvyšovala, jak je tomu obvykle, ale snížila se kvůli numerickým chybám.

Vysokotlaká fáze vodního ledu VII.

Kokrystaly a soli

Molekulární krystaly nemusejí být tvořeny pouze jednou látkou, ale mohou obsahovat dvě nebo více složek. Tyto tzv. kokrystaly jsou zajímavé například pro farmaceutický průmysl. První složkou je léčivo a vhodnou volbou druhé složky je možné měnit vlastnosti jako rozpustnost. Stejně jako jednosložkové molekulární krystaly jsou i molekuly v kokrystalu vázány nekovalentními vazbami, tedy pomocí vodíkových můstků, dalších elektrostatických interakcí a elektronových korelací. Velmi zajímavé jsou kokrystaly s vodíkovými můstky mezi kyslíkem a dusíkem, tedy vazbami O–H … N. V případě této vazby může někdy dojít k odštěpení jádra vodíku z první složky a jeho přesunu na složku druhou. Jelikož se přesouvá jen kladně nabité jádro, a ne i elektron, získá jedna složka náboj záporný a druhá kladný, čímž vznikne krystal soli. Zajímavost těchto systémů spočívá v tom, že není jednoduché určit experimentálně, zda k přenosu došlo, a také teoretické metody nejsou pro předpověď přenosu prozatím spolehlivé.

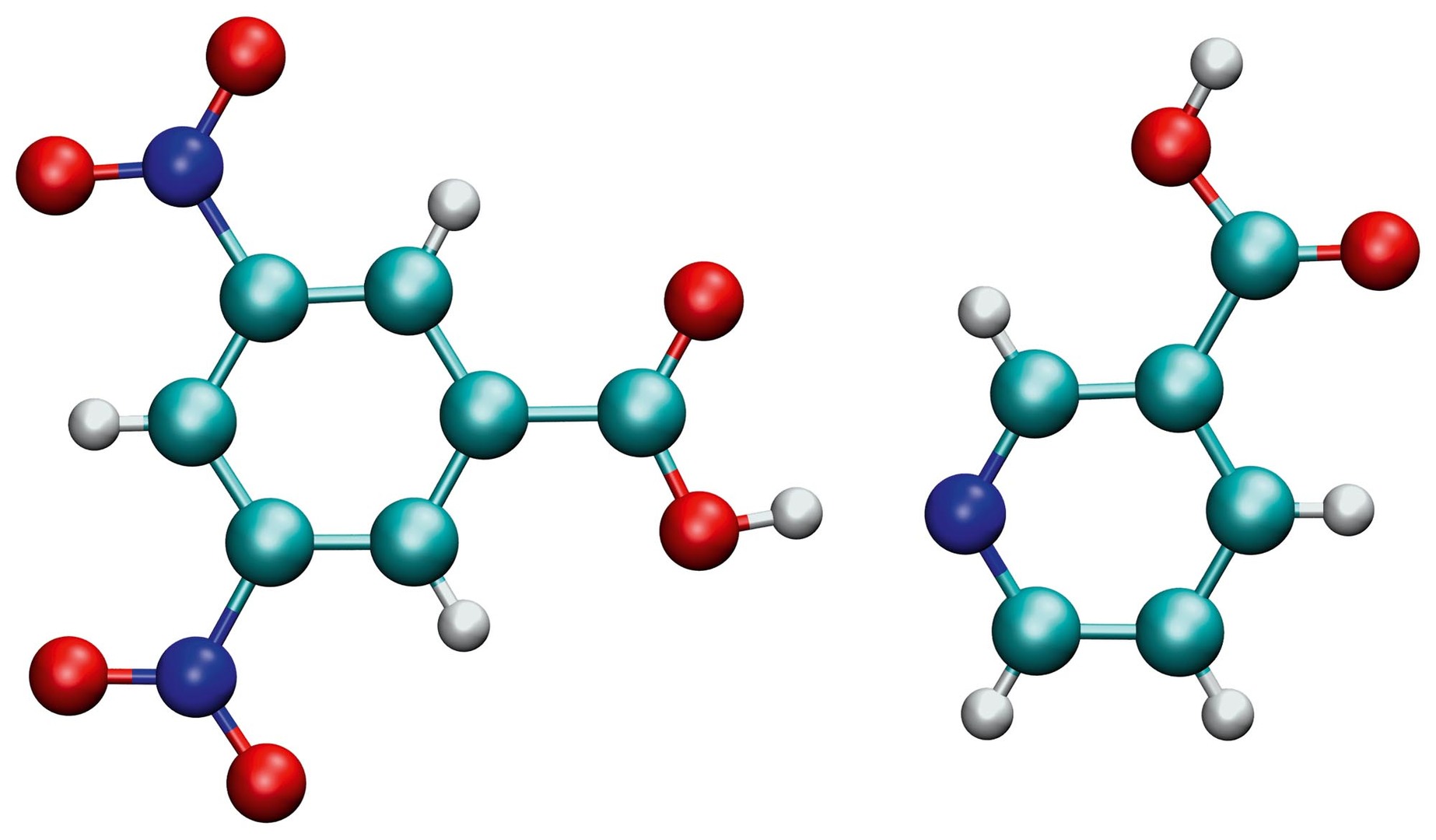
Příklad vodíkové vazby, u které může v krystalu dojít k přenosu, je na obr. 2. Molekula vlevo je kyselina dinitrobenzoová, molekula vpravo kyselina nikotinová (niacin). Na základě dat z rentgenové krystalografie byl tento systém klasifikován jako kokrystal, tedy bez přenosu jádra vodíku. Pozdější práce využívající neutronovou krystalografii, která umožňuje lépe zjistit polohu vodíku, a další měření [2] ale určily, že k přenosu jednoznačně dochází. Tato situace byla nepříjemná pro tvůrce teoretických metod, kteří se snažili, aby jejich metoda přenos nepředpovídala.

Jednou z velkých výhod počítačových simulací je možnost plně udat strukturu systému. Pro kokrystaly tedy můžeme vodík postupně přesouvat z molekuly první složky na druhou molekulu a při každém kroku vypočítat energii systému. Z těchto dat můžeme zjistit, která pozice je pro vodík výhodnější, tedy zda má nižší energii kokrystal, nebo sůl. Dále zjistíme, zda mezi kokrystalem a solí existuje energetická bariéra. Problém je ale v tom, že různé teoretické metody dávají pro energetickou závislost přenosu vodíku různé předpovědi. Pokud uvažujeme metody založené na jednočásticové aproximaci, tak standardní přístupy DFT energeticky zvýhodňují přenos vodíku, tedy vznik soli, zatímco Hartreeho-Fockova metoda preferuje kokrystaly. Rozdílnost předpovědí patrně souvisí s tím, že aproximace DFT mají problém lokalizovat elektrony, zatímco metoda HF lokalizaci preferuje. V praxi se často využívají metody kombinující oba přístupy a ty by měly být vhodné i pro řešení problému pozice vodíku.

Fáze molekulárních krystalů

Ze školy nebo ze života známe čtyři skupenství hmoty: pevné, kapalné, plynné a plazmu. Nicméně mnoho molekul má více pevných fází existujících za různých tlaků a teplot a navzájem se lišících strukturou. Například pro vodu jich je známo přes deset. Předpověď stabilních fází a rozsahu teplot a tlaků, za kterých budou existovat, je jedním z otevřených problémů současných simulací, i když ne neřešitelným [3].

Obecně platí, že se vzrůstajícím tlakem se snižuje objem připadající na jednu molekulu, tedy zvyšuje se hustota. U vody se to děje zajímavým způsobem. V každé fázi tvořené molekulami se každá z nich stále účastní čtyř vodíkových vazeb, ale při změně fáze se vzdálenost mezi kyslíky tvořícími vodíkovou vazbu nezkracuje. Naopak vzdálenost mezi sousedními kyslíky při změně fáze trochu roste. Snižuje se ale vzdálenost k dalším molekulám, což je výhodné z hlediska elektronových korelací.

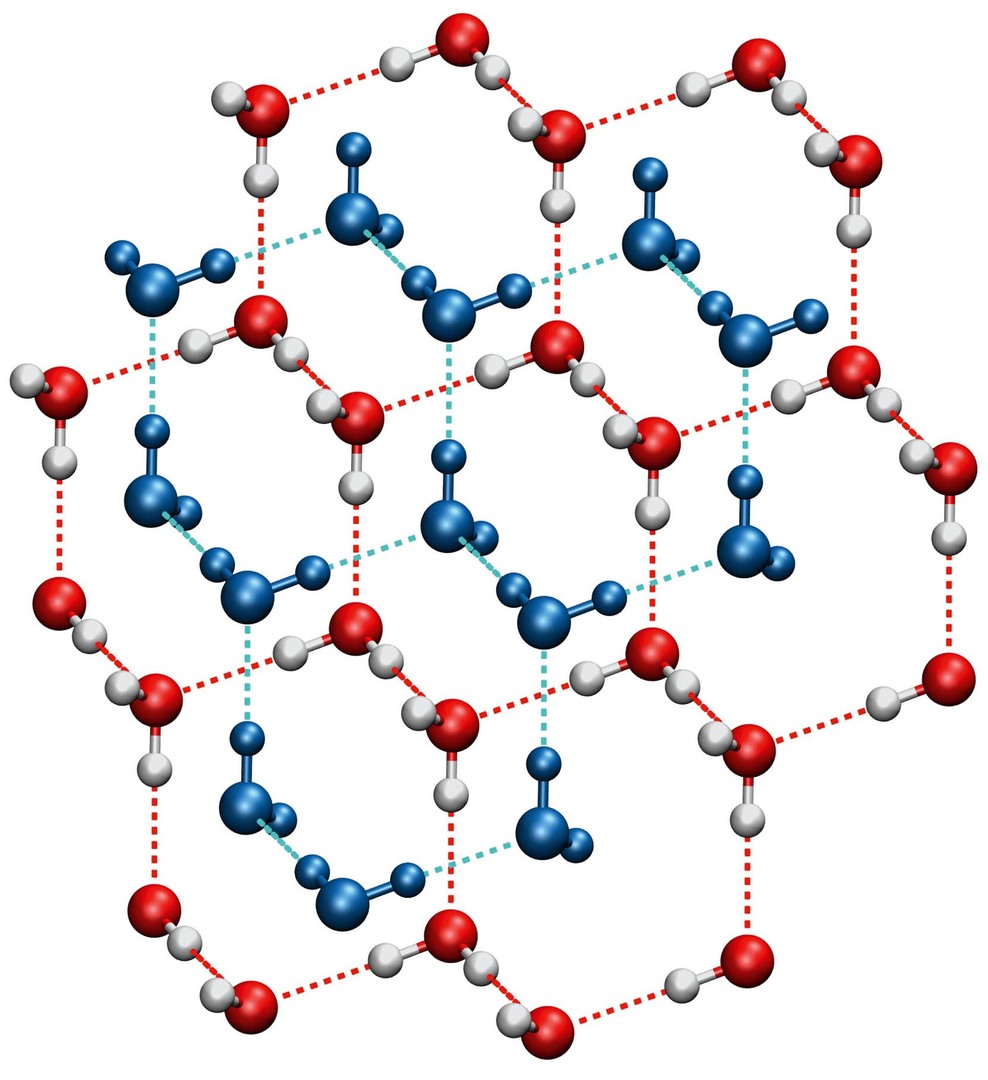
Nám známý led je označován jako fáze Ih. Ve své struktuře obsahuje molekuly uspořádané přibližně do tvaru šestiúhelníků tvořících jakousi trojrozměrnou síť [4]. V ní je hodně volného místa, což není se vzrůstajícím tlakem výhodné. Pro vodní led existuje zajímavá vysokotlaká fáze VII, stabilní při tlacích vyšších než přibližně 2 GPa. Struktura ledu VII je tvořena dvěma do sebe vnořenými strukturami ledu Ih (obr. 4). Volné místo je tedy využito další sítí molekul.

K další zajímavé změně struktury dojde při zvýšení tlaku přes 62 GPa. Při těchto tlacích jsou vzdálenosti mezi kyslíky tvořícími vodíkový můstek tak malé, že přestane existovat bariéra pro pohyb vodíku mezi oběma kyslíky. Atom vodíku se poté nachází uprostřed mezi oběma kyslíky. Nejedná se už potom o fázi tvořenou molekulami vody, ale o jakousi trojrozměrnou mříž atomů kyslíku, které sdílejí vodíky.

Experimenty provedené v poslední dekádě navíc naznačují, že při dalším zvýšení tlaků a teplot se kyslíková mříž zachová, ale vodíky se v ní začnou volně pohybovat. Takovéto fázi potom říkáme superionická a pro vodu nebo amoniak může existovat na vnějších planetách sluneční soustavy.

Z hlediska výpočtů je popis různých fází molekulárních krystalů obtížný, neboť vyžaduje velmi přesné výpočty pro systémy s mnoha atomy. Navíc energetické rozdíly mezi různými fázemi jsou velmi malé v porovnání s vazebnou nebo celkovou energií. Pro představu: u dvou extrémů u vodního ledu, tedy fází Ih a VIII, poklesne vazebná energie z hodnoty 59 kJ/mol jen o cca 3 kJ/mol. Tento malý rozdíl energií přitom není způsoben jen poklesem síly vodíkové vazby se vzrůstajícím tlakem. Pro fáze stabilní za vyšších tlaků roste důležitost elektronových korelací, které pokles síly vodíkových vazeb kompenzují. Pro přesné určení rozdílu energií mezi fázemi je tedy nutné použít metody, které popisují přesně jak vodíkové vazby, tak elektronové korelace.

Od teorie k praxi

Molekulární krystaly jsou velmi rozšířené systémy a jejich studium umožňuje pochopit přesnost teoretických metod a jejich počítačových implementací. Spolehlivější metody potom umožňují ověření nebo vysvětlení experimentálních pozorování a přírodních nebo průmyslových procesů, ve kterých molekulární krystaly vystupují.