Co je to kinetické Monte Carlo

Bereme jako samozřejmost, že jakoukoliv barvu, kterou člověk vnímá, lze složit ze tří základních barev (červená, zelená, modrá – stačí se podívat lupou na obrazovku počítače nebo televize). Přitom naši vzdálení příbuzní, plazi a ptáci, vidí (zpravidla) barvy čtyři, většina savců však jen dvě. Čtyřbarevné vidění je evolučně starší. Savci totiž v průběhu skrytého nočního života ve stínu krvelačných praještěrů dva pigmenty ztratili. My a většina primátů Starého světa vidíme barvy tři, protože dlouhovlnný pigment se v důsledku mutace rozdělil na dva. Obě varianty mají sice překrývající se křivky citlivosti s blízkými maximy, takže hardwarově na tom nejsme nijak slavně, náš mozek však disponuje softwarem, který si s tím poradí. Oba geny jsou na pohlavním chromozomu X, takže pokud dojde k závadě, jsou na tom ženy lépe, protože mají tyto chromozomy dva. Proto je také červenozelená barvoslepost rozšířenější u mužů.

Evoluce u opic Nového světa se prodírala jinými cestičkami.¹⁾ Samci nerozlišují červenou a zelenou vůbec a jedna třetina samic také ne. Pouze asi dvě třetiny samic mají plné trichromatické vidění. Je to proto, že v populaci se u jediného genu pro dlouhovlnný pigment (opakuji, že my máme tyto geny dva) vyskytují tři alely, jejichž spektrální citlivosti se poněkud liší. Samci mají jeden chromozom X, a proto jen jednu variantu pigmentu a nemohou vidět tříbarevně. Samice mají pohlavní chromozomy X dva, a pak záleží na tom, jaké alely se sejdou. Pokud se sejdou dvě stejné, je opička také barvoslepá. Pokud se sejdou dvě různé, rozlišuje opice červenou a zelenou; to nastane ve dvou třetinách případů.

Z tohoto líčení není ale zřejmé, jakým mechanismem se po dobu desítek milionů generací udržuje v populaci rovnoměrné zastoupení tří alel (označme je A, B a C). Zřejmě je jistou výhodou být schopen rozlišit červené a žluté ovoce, ale jak se tato výhoda projeví na potomstvu? Problém mi vrtal hlavou, a tak jsem se rozhodl využít počítačových simulací, metodu nazvanou po slavném kasinu Monte Carlo. Živím se totiž simulováním molekul, a ono je z technického hlediska skoro jedno, jestli nahradím molekuly opicemi.

Nejjednodušší typ modelu pracuje po generacích. V jedné generaci se jedna samice spáří s náhodně vybraným samcem a může porodit jednoho potomka. Aby počet opic nerostl exponenciálně nade všechny meze, což by vedlo k ekologické katastrofě (v přírodě i na počítači), nemohou se narodit všechna mláďata. Předpokládejme, že limitující je množství potravy a že potomek s určitou pravděpodobností úměrnou celkovému počtu žravých opic zahyne hlady. Evoluční výhoda barevného vidění je reprezentována tím, že pravděpodobnost přežití potomka lépe vidoucí opice je o malinko větší než u opice barvoslepé.

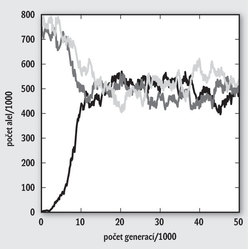
Na obrázku je ukázán vývoj počtu jednotlivých alel v populaci milionu opic, jestliže na začátku byla alely A jen desetina procenta, B a C byly zastoupeny stejně a pravděpodobnost přežití potomka trichromatické opice je o pouhých 0,1 % větší než dichromatické. Opice žije deset generací. Vidíme, že po počátečním váhání dojde k rovnoměrnému rozprostření alel v populaci. Pro uvažované počáteční podmínky a velmi malou výhodu barevného vidění je začátek kritický, ve ¾ případů (z 50 simulací) dokonce došlo k vymizení alely a jen ¼ se ujala. Příroda musí trpělivě zkoušet několikrát. Není-li však barevné vidění žádnou výhodou, vymizí alela ve 100 % případů.

Kvalitativně se výsledky modelu dají vysvětlit uvažováním z hlediska genu, který je, jak známo, sobecký. Je-li např. málo alely A, pak s velkou pravděpodobností narazí při páření na B nebo C a usadí se v úspěšnější opici s kombinací alel AB nebo BC. Je-li alely A hodně, zvyšuje se pravděpodobnost, že se setká s A.

Model je maximálně zjednodušený a jistě ho lze libovolně zesložitit, např. realističtějšími pravidly přežívání opic v závislosti na zdrojích, modelováním proměnného přísunu potravy, výběrem partnera z okolí a zavedením migrace atd. Avšak čím jednodušší model, tím lépe pochopíme, jak vlastnosti jednotlivce vedou k chování komplexního systému.

Simulační metody založené na pojmu náhodné události, ke které dojde za určitých podmínek s určitou pravděpodobností, se ve fyzice a chemii nazývají kinetické Monte Carlo. Lze jimi studovat třeba růst krystalu po jednotlivých atomech či postup polymerace (monomery přidifundují a zreagují), hromadnou obsluhu (zákazníci přijdou a jsou obslouženi) a vůbec ekonomii (ale pozor, na rozdíl od fyziky, kde máme zákon zachování energie, zde žádný zákon zachování peněz neplatí), vznik dopravní zácpy a mnoho dalších jevů. Obecně nás zajímá chování složitého systému v průměrném (statistickém) smyslu, jestliže známe mechanismy vzájemného působení jednotlivých částí.