Jedenapůlrozměrný prostor

Jedním z mocných prostředků, jichž matematici používají k objevování nových zákonitostí i teorií, je zobecnění. Běžnější podobu zobecnění sdílí matematika s jinými vědami: na základě nějakého počtu případů (konečného i nekonečného) se formuluje obecná zákonitost, hypotéza. Připomíná to indukci, ale na rozdíl od jiných věd se matematici nikdy nespokojí se sebevětším počtem potvrzení (verifikací), nýbrž usilují o důkaz nebo vyvrácení pomocí protipříkladu.

Tak třeba Pierre Fermat (1601–1665) usoudil, že rovnice xⁿ + yⁿ = yⁿ nemá celočíselná řešení pro n > 2, a zřejmě tak učinil na základě velmi malého počtu příznivých případů.

V dalších staletích se nahromadila obrovská evidence ve prospěch této hypotézy a nedařilo se najít protipříklad. Všichni byli přesvědčeni o platnosti této hypotézy, jenže přesvědčení matematikům právem nestačí. Ulevilo se jim, až když před nějakými deseti lety tuto hypotézu řádně dokázal Andrew Wiles (viz Vesmír 73, 31, 1994/1).

Týž Fermat se domníval, že 2²ⁿ + 1 je prvočíslo pro každé n:

2²¹ + 1 = 5, 2²² + 1 = 17, 2²³ + 1 = 257, 2²⁴ + 1 = 65537,

a všechno to skutečně prvočísla jsou. Příběh této hypotézy byl kratší, ne však tak krátký, jak bychom snad čekali. Trvalo nějakých dalších sto let, než Leonharda Eulera (1707–1783) napadlo vyzkoušet hned další případ:

2²⁵ + 1 = 4294967297,

který tuto hypotézu vyvrátil; toto číslo je dělitelné 641, přijít na to ovšem vyžaduje jistou vynalézavost.

Někteří matematici a filozofové (zvláště pak Imre Lakatos) z takových případů soudili, že matematika má „kvaziempirickou“ povahu, že aspoň k některým objevům se dochází podobně jako v empirických vědách indukcí z jednotlivých případů. V obou případech je to klam, protože skutečný objev předchází použití indukce: napřed musíme mít hypotézu, abychom vůbec věděli, na co máme indukci použít. Klam pochází ze zpětné rekonstrukce: předvede se řada příznivých případů a „každý hned vidí“ – podobě jako v testech IQ – jak to bude pokračovat a jak to zobecnit. K tomu, abychom to jako klam rozpoznali, stačí si jen položit otázku: tak proč na to přišel až Fermat, Euler…

Matematika však používá zobecnění i jiným způsobem, který se v jiných vědách nevyskytuje a který by bylo možno nazvat spíše rozšíření. Tím se zde myslí rozšíření na větší oblast platnosti, na oblast „obecnější“. Taková zobecnění neslouží jen k projasnění předpokladů (například co je skutečně zapotřebí předpokládat k důkazu nějaké věty), nýbrž napomáhají – téměř zázračně – k vyřešení problémů, které se v původní zúžené podobě zdály být obtížně řešitelné. Příkladů takových úspěšných (a začasté neobyčejně krásných) zobecnění je v matematice mnoho, nikdy jsem však nenašel žádné kloudné vysvětlení úspěšnosti takových zobecnění; říci, že se při nich potlačí nepodstatné konkrétnosti, které mohly působit jako zábrana, mi připadá spíše jako odbytí. Někdy je takové zobecnění nejen krásné a pomůže vyjasnit a vyřešit dřívější problémy, nýbrž otevře zcela novou oblast poznání. Jedno takové zobecnění zde chci vyložit. Je to zobecnění matematikům a duším spřízněným dobře známé; jim ovšem tento článek určen není. Určen je spíše těm, kteří z tohoto zobecnění znají jen některé vedlejší důsledky, mámivé obrázky, a cílem je ukázat, že se za těmito obrázky, pod jejich povrchním povrchem, skrývá něco mnohem krásnějšího. Zkrátka poukázat na rozdíl mezi krásou, která sousedí s pravdou, a mámivostí, která je hned vedle mamu a klamu.

Začneme příkladem dobře známých zobecnění. Vlastně, jsou opravdu dobře známá? Je jasné, že třeba a⁵ je zobecněním? Přece není nic jednoduššího: a·a značíme a², součin tří a pak a³ a obecně aⁿ součin n čísel či veličin a. A hned je také jasné, že součin n čísel a vynásobený součinem m čísel a je totéž jako součin (n+m) čísel a: aⁿ · a^m = a^(m+n). To je vše samozřejmé. Opravdu? Tak jak je možné, že neschopnost udělat takové zobecnění dokázala zablokovat rozvoj geometrie na téměř dvě tisíciletí? Proč se muselo čekat až na Descarta? Za okamžik se k tomu vrátím. Teď se podívejme na další zobecnění: co by mohlo být třeba a^1,5? Nemůžeme na to jít otázkou: co to znamená vynásobit 1,5krát a samo sebou. Lepší je říci si: mocniny s neceločíselnými exponenty by měly splňovat táž pravidla, která splňují mocniny s celočíselnými exponenty. Tak by mělo platit a^1,5 · a^1,5 = a^1,5 + ^1,5 = a³. Pak ovšem mám hned důsledek: a^1,5 = √a³ Odtud je už jen krůček k obecnému případu: (a^m/n)ⁿ = a^m/n.n = a^m, takže a^m/n = ⁿ√a^m Pokračování je v učebnicích.

Vraťme se k původnímu zobecnění – mocninám s libovolným celočíselným exponentem. Mocniny se vykládaly geometricky: je-li x délka úsečky, je x² plošný obsah čtverce se stranou x a x³ je objem krychle. Co je ale x⁴? Měl by to být objem čtyřrozměrné krychle, jenže tomu nic v přirozené geometrii neodpovídá. To byl problém řecké geometrie, kterou trápil i obecnější problém, totiž jak geometricky interpretovat „součin“ čtyř úseček. Takový součin se v geometrii vyskytl jen jednou, a to ve slavném Hérónovu vzorci pro plošný obsah trojúhelníku (připomenu: má-li tento trojúhelník strany a, b a c a polovinu jeho obvodu si označíme s =1/2( a + b + c), pak je plošný obsah roven √s(s-a)(s-b)(s-c)).

Descartova revoluce v matematice spočívala v nastoupení přesně obrácené cesty: z x², x³, x⁴ atd. udělal úsečky a začal s nimi algebraicky počítat. Tak vytvořil algebraickou geometrii (nikoli analytickou, jak se stále chybně opakuje). Toto zobecnění mu nejen dovolilo vyřešit problémy, které trápily řeckou geometrii, ale i otevřít cestu k obrovskému rozvoji jak geometrie, tak matematiky vůbec.

Současně to však dovolilo se vrátit (ovšem až v 19. století) k původní interperetaci a tu zobecnit, tj. zobecnit pojem prostoru. Můžeme-li ztotožnit rovinu s uspořádanými dvojicemi reálných čísel (souřadnic bodů) a vytvořit prostor s trojicemi, můžeme n-rozměrný prostor ztotožnit prostě s uspořádanými n-ticemi reálných čísel a přenést tam i ostatní pojmy z rovinné a prostorové geometrie. (Občas někoho napadne, že by se v takovém čtyřrozměrném prostoru dobře kradlo z uzavřených skladů, nenapadne ho však, že by se v takovém prostoru změnila i fyzika – a mimochodem, že by takto krást mohl jen maximálně třírozměrné předměty, které mu ve čtyřrozměrné zastavárně nevezmou.)

Potud to bylo vše dobře známé a bylo to spíše jen připomínkou, jak se v matematice zobecňuje a jak nám připadá samozřejmé to, co vůbec samozřejmé nebylo. A také to byla příprava na následující otázku. Co je x^1,5 v Descartově algebraické geometrii, víme (je to opět úsečka). Ale co by to mohlo být v druhé interpretaci, v níž exponent n v xⁿ je dimenze prostoru (či geometrického útvaru)? Existuje nějaký jedenapůlrozměrný útvar a jak by mohl vypadat? A lze tomu vůbec dát nějaký smysl? Uvidíme, že ano, ale že budeme muset nejprve nalézt nějakou jinou charakterizaci dimenze, která by se pak dala zobecnit. Bude to ovšem muset být nějaká hodně neobvyklá charakterizace – a přitom charakterizace, která – až bude prozkoumána – nám bude připadat „přirozená“.

Tato charakterizace se zakládá na tom, že při změnách měřítka zůstává něco nezměněno. Začněme úsečkou. Zmenšíme-li ji k-krát, dostaneme úsečku, která se podobá úsečce původní, do níž se vejde N-krát; zde je ovšem N = k. „Vejde“ zde znamená, že původní úsečku bezezbytku pokryjeme N-zmenšenými úsečkami. U obdélníku je tomu podobně: dostaneme menší obdélník, který je podobný původnímu, do nějž se vejde N = k²-krát (obrázek). U kvádru bude N = k³. A mohli pokračovat obecně n-rozměrným prostorem, bylo by tam N = kⁿ.

Všimněme si dvou věcí, které jsou zde tak samozřejmé, že se upozornění na ně zdá být ostudné. Zaprvé tento postup můžeme opakovat; výsledný útvar (třeba mřížku výše) můžeme opět zmenšit (na obrázku výše bylo zmenšení 1 : 4, teď bude 1 : 4²) a výsledkem pokrýt opět výchozí obdélník – teď bude mřížka mnohem hustší. Zadruhé dimenze n vystupuje jako exponent ve vztahu N = kⁿ.

Právě tyto dvě vlastnosti nabízejí cestu k zobecnění, které by nás přivedlo k útvarům s neceločíselnou dimenzí. Jak by takový útvar musel vypadat? Zaprvé by musel splňovat podmínku, že po (vhodném – to ještě upřesníme) zmenšení jím bude možné „pokrýt“ původní útvar, a navíc že to budeme moci opakovat donekonečna (pro stále menší zmenšeniny) – tedy že výsledný útvar bude „soběpodobný“, jeho sebemenší části budou podobné původnímu útvaru. A zadruhé by měl platit vztah mezi počtem N zmenšenin nutných k pokrytí a zmenšením k samým, totiž vztah N = k^d, v němž by d už nebylo celé číslo. Toto d bychom pak mohli nazvat dimenzí výsledného útvaru. To je ovšem jen hrubá idea a její popis, ale následující příklad do toho (snad) vnese jasno. Vyjdeme z úsečky, kterou rozdělíme na čtyři stejné části a prostřední dvě části „zalomíme“ tak, jak je to ukázáno na následujícím obrázku:

Výsledek nyní zmenšíme třikrát (k = 3):

Touto zmenšenou kopií dokážeme pokrýt původní útvar (musíme použít N = 4 kopií):

Zmenšený původní útvar můžeme znovu zmenšit třikrát (tj. výchozí útvar devětkrát) a opět jím pokrýt druhý výsledný (už jednou pokrytý) útvar. Budeme k tomu potřebovat N = 4² = 16 podruhé zmenšených útvarů:

Tak můžeme pokračovat do nekonečna. Ukážeme si ještě jednu iteraci, u níž potřebujeme N = 4³ = 64 zmenšenin:

Každý jednotlivý útvar v této řadě iterací je obyčejná lomená čára a má přirozeně dimenzi 1. Žádný z nich nesplňuje naši podmínku, že sám se uvnitř opakuje donekonečna, že je „soběpodobný“. Tuto podmínku splňuje až limita těchto křivek, tedy výsledek iterací dovedený myšlenkově „donekonečna“, a teprve pro tento výsledný útvar můžeme počítat dimenzi. Máme N = 4 a k = 3 (při dalších zmenšeních je N = 4ⁿ a k = 3ⁿ) a podle našeho zobecnění je dimenze tohoto útvaru exponentem d ve vztahu N = k^d, tj. 4 = 3d. Numerickou hodnotu d dostaneme jednoduše logaritmováním: d = logN/logK = log4/log3 = 1,26186...

Zobecněná dimenze této limitní křivky je tedy neceločíselná (dokonce je iracionální a snadno se to dokáže). Podle očekávání je menší než 2, protože jde o útvar v rovině. Kdyby tomu tak nebylo, mohli bychom naše zobecnění rovnou hodit do koše. Je však větší než 1: limitní křivka je tak jemňounce „hrbatá“, že je mírně rozmazaná – jak moc, to říká právě číslo 1,26186… Kdybychom za výchozí útvar („generátor“) vzali analogický „dvouhrbý“ útvar (měli tak N = 7, k = 5), dostali bychom méně rozmazanou křivku (s menší dimenzí); se zvětšováním počtu hrbů by se limitní křivka stávala stále méně rozmazaná (dimenze by se blížila 1), až by to v limitě byla prostě úsečka. Právě experimentování s různými generátory nás postupně přesvědčuje, že takové zobecnění vyjadřuje něco hlubšího a není to jen nějaká hříčka. Můžeme se vydat také obráceným směrem a křivky stále více rozmazávat, tj. jejich dimenze zvětšovat až k 2. Uvedeme si hned jeden takový příklad. Výchozím útvarem (generátorem) je tato lomená čára, za ní pak následují první dvě iterace: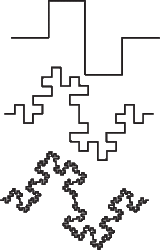

Máme zde N = 8 (prostřední svislá úsečka generátoru je tvořena dvěma úsečkami) a k = 4, takže dimenze limitní křivky je d = logN/logk = log8/log4 = 1,5.

Dimenze můžeme zvyšovat až do 2; slavná Peanova křivka zaplňující čtverec má dimenzi přesně 2.

Předcházející výklad byl tak trochu rekonstrukcí. Historicky zde byly nejprve některé podivné křivky, teprve daleko později přišel pojem zlomkové či fraktální dimenze. První křivka pochází z roku 1904, kdy ji sestrojil H. von Koch jakožto elementární geometrickou konstrukci křivky (funkce), která nemá v žádném bodě tečnu (i když je spojitá, nemá v žádném bodě derivaci). Takovou křivku (jinými prostředky, ne tak elementárními) sestrojil Karl Weierstrass a před ním i Bernard Bolzano. Von Kochova křivka (to byl náš první příklad) se pro větší vizuální působivost kreslívá většinou tak, že se tři její generátory spojí do trojúhelníku, a pak se všechny současně zjemňují; dostane se něco jako „sněhová vločka“ (výsledek si račte představit sami).

Von Kochova křivka má řadu dalších zajímavostí. Například je nekonečně dlouhá. Má-li výchozí úsečka délku 1, má generátor délku 4/3. Další iterace se skládá ze 4 částí, z nichž každá je předchozí křivkou třikrát zmenšenou, takže její délka je 4 .1/3.4/3 = (4/3)². n-tá iterace má pak délku (4/3)ⁿ a tato délka roste s n do nekonečna. Nekonečná je i vzdálenost kterýchkoli dvou bodů této křivky (je mezi nimi vždy jedna celá zmenšená limitní křivka, jejíž délka je ovšem také nekonečná, neboť zmenšením nekonečna dostaneme zase nekonečno). A nakonec je zde vlastnost „soběpodobnosti“: jakkoli malý kousek křivky obsahuje v sobě část, která je věrnou zmenšenou kopií původní křivky.

Takové křivky byly dlouho vnímány jako monstra či patologické případy, které měly přinejlepším nabádat k opatrnosti při důkazech matematických vět a nespoléhat se na názorné představy a obrázky. Do vlastní matematiky však nepatřily. Známá jsou slova Charlese Hermita (v dopisu Thomasu J. Stieltjesovi), jimiž se s „hrůzou a odporem odvrací od funkcí bez derivace“.

Taková „monstra“ se čas od času objevovala v různých oblastech vědy, bývala však považována v souladu s panující tradicí za něco okrajového a spíše výjimečného. Systematicky je začal rehabilitovat, jak je dobře známo, až Benoît Mandelbrot, který pro ně vymyslel název fraktály. A nejen je rehabilitoval, nýbrž přišel i s myšlenkou, že by tomu mohlo být zcela naopak, totiž že monstry by mohly být spíše přímky, kružnice a dokonale hladké křivky, protože sama podstata přírody je fraktální. Začal pak hovořit o fraktální geometrii přírody. K tomu, aby byl takový obrat úspěšný, je zapotřebí souhry přiznivých okolností a také jisté propagace (či dokonce propagandy). V případě fraktálů k tomu přispěly počítače, které je dovolily barevně vizualizovat. Všichni známe pestrobarevné obrázky podivuhodných útvarů, jimiž lze cestovat do hloubky, abychom tam objevovali další a další podivuhodné útvary. Podmalováno vhodnou hudbou je to velice působivé – až do okamžiku, kdy zjistíme, že je to velmi nudné.

Pro značnou část matematiků jsou fraktály stále něčím na okraji matematiky; tak silná je jistá tradice (či paradigma). Nepochybně k tomu přispěl i Mandelbrotův styl výkladu: velmi neformální (nikdy se netajil svým odporem k formalizované matematice), plný metafor.

Mandelbrotovu původní a stále znovu vydávanou knihu o fraktálech (Les objets fractales – Forme, hasard et dimension) jsem přeložil ¹⁾ a před časem ji vydalo nakladatelství Mladá fronta. V „poznámce překladatele“ jsem napsal právě něco k tomuto „nepřesnému“ Mandelbrotovu stylu a dovolím si to tady na závěr zopakovat:

Méně srozumění vyvolává Mandelbrotův odpor vůči přesnosti a přísnosti – jak jsme na ni zvyklí v matematice. „Nematematický“ čtenář by si zde mohl s úlevou pomyslet: „Díky Bohu, aspoň tomu budu lépe rozumět.“ Bohužel opak je pravdou: Mandelbrotův styl toho vyžaduje od čtenáře více, než kdyby dodržoval některé zvyklosti. Mnohokrát jsem měl pocit, že leccos mohl říci jasněji (tj. přesněji), někdy jsem měl pokušení napravit to; zůstal jsem ale loajálním překladatelem, a navíc jsem si na víc netroufal. Jenže z druhé strany: právě takovou povahu měla většina „paradigmatických“ matematických (a nejen matematických) děl. Příkladem může být Descartova Geometrie, která jeho učené současníky rozčilovala (zvláště asi jeho opakované „už mne nudí podrobně vše vykládat, dodělejte si to sami“) tak, že mu nikdy neotevřeli brány Sorbonny. Dodělali to, udělali z toho učebnice, rozvíjeli to dál, velice to obohatili. Jen Descartes však otevřel zcela nové vidění světa.

Dnes jsme tolerantnější. Zpřesňující práce jsou v chodu, jejich výsledek však asi už nebudeme číst s tím potěšením, které nám připravil Mandelbrotův „esej“.

Mandelbrot nám také chce otevřít radikálně jiné vidění světa. Nechce nás něčemu „naučit“. Chce nám ukázat, že příroda je mnohem bohatší, než aby na ni stačila jen stará geometrie, a že tou opravdovou elementární geometrií je „fraktální geometrie přírody“. Chce změnit naše myšlení.