Benfordův zákon
| 5. 10. 1998Položme si otázku: Vezmeme-li větší skupinu dat (řekněme 1000) reprezentujících jakoukoliv přírodní veličinu (například soubor fyzikálních konstant nebo ceny zboží v místním supermarketu), jaká je pravděpodobnost, že určité číslo bude začínat jedničkou? Na první pohled je odpověď jasná: Počáteční číslovka může být 1, 2, 3,... až 9 (vyloučíme nulu, která může být libovolně přiřazena před jakékoliv číslo). Tedy pravděpodobnost výskytu jakékoliv číslovky na prvním místě je 1/9 = 0,111 neboli 11,1 %. Takže z 1000 čísel by 11,1 %, tj. zhruba 111 čísel, mělo začínat jedničkou (stejně jako dvojkou, trojkou atd.). Opravdu?
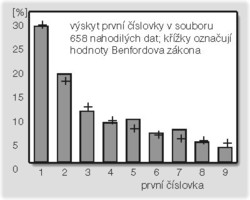
„Omyl,“ říká Benfordův zákon. Ve skupině čísel reprezentujících reálné hodnoty čehokoliv je asi 30% pravděpodobnost, že první číslovkou bude jednička! Dále pak 17,6 % čísel bude začínat dvojkou, 12,5 % trojkou a jen 4,57 % devítkou. To znamená, že z 1000 čísel v průměru 300 bude začínat jedničkou, 176 dvojkou a pouze 46 bude mít na prvním místě devítku.
Nejde o žádný matematický trik, ale o skutečný přírodní zákon, jímž se řídí soubory jakýchkoliv přirozených dat, bez ohledu na jejich podstatu nebo fyzikální jednotky. Jedinou podmínkou je, že data musí být v minimálním rozsahu tří logaritmických intervalů (tj. v minimálním rozsahu tří desítkových řádů).
V přiloženém grafu (vpravo dole) je znázorněn výskyt prvních číslovek v souboru dat obsahujících počty obyvatel v 658 světových městech. Jasně vidíme, že jednička převládá zhruba ve 30 % případů. Podle Benfordova zákona procentuální pravděpodobnost p (%) výskytu číslovky D (tj. 1, 2, 3, 4, 5, 6, 7, 8, 9) na prvním místě v libovolném souboru dat se dá vypočítat z rovnice:
p (%) = 100 log [1+ (1/D)].
Podstatu tohoto jevu lze lehce pochopit z pohledu na logaritmickou stupnici: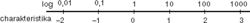 Interval odpovídající každé charakteristice má stejnou délku, ale nelineární rozdělení mantisy (desetinné části logaritmu) uvnitř intervalu:
Interval odpovídající každé charakteristice má stejnou délku, ale nelineární rozdělení mantisy (desetinné části logaritmu) uvnitř intervalu: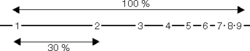
Délka intervalu v každé mantise mezi 1 a 2 je zhruba 30 % délky každého charakteristického intervalu. Skupina přirozeně nahodilých dat přesahujících několik charakteristických intervalů má tedy 30% šanci zapadnout mezi hodnotu 1–2 (tj. počáteční číslovka je 1) a pouze 4,6% možnost zapadnutí do intervalu počínajícího číslem 9.
Tuto skutečnost poprvé zveřejnil matematik Newcombe v článku nazvaném Note on the Frequency of Use of the Different Digits in Natural Numbers, který byl publikován v American Journal of Mathematics (1881) 4, 39–40. Newcombův článek ale upadl v zapomnění a tento přírodní jev znovu objevil r. 1938 fyzik Frank Benford. Všiml si zajímavé skutečnosti, že logaritmické tabulky v technické knihovně měly mnohem víc ohmatané stránky s čísly počínajícími jedničkou. Benford svá zjištění publikoval v článku pod názvem The Law of Anomalous Numbers v Proc. Amer. Phil. Soc. 78, 551–572.
Výskyt první číslovky v souboru nahodilých dat se dá graficky znázornit histogramem: Aplikace Benfordova zákona je dalekosáhlá. Máme-li větší soubor jakýchkoliv dat, můžeme poměrně jednoduchým statistickým rozborem lehce zjistit, jsou-li data skutečná (přírodní), nebo podezřelá. Například vezmeme-li vyplněný formulář daňového přiznání, správně vyplněné údaje by měly víceméně zapadat do Benfordova statistického výskytu první číslovky. Stejně tak se dají analyzovat výsledky voleb, vědecká data, ekonomické údaje apod.
Aplikace Benfordova zákona je dalekosáhlá. Máme-li větší soubor jakýchkoliv dat, můžeme poměrně jednoduchým statistickým rozborem lehce zjistit, jsou-li data skutečná (přírodní), nebo podezřelá. Například vezmeme-li vyplněný formulář daňového přiznání, správně vyplněné údaje by měly víceméně zapadat do Benfordova statistického výskytu první číslovky. Stejně tak se dají analyzovat výsledky voleb, vědecká data, ekonomické údaje apod.
Platnost Benfordova zákona si může ověřit každý, kdo má i laciné PC nebo lepší kalkulačku. Počet dat ve zvoleném souboru nemusí být velký – už i 100 číselných údajů poskytuje poměrně dobrý souhlas s výše uvedeným statistickým rozdělením. Pochopitelně ale platí základní pravidlo statistiky: Čím více dat, tím lepší souhlas s teoretickou křivkou.
Benfordův zákon se bohužel nedá použít k zlepšení šance výhry v Sazce, protože nahodile tažená čísla 1 až 9 mohou být seřazena v libovolném pořadí. V každém případě je však Benfordův zákon fascinující a je zajímavé, jak málo i renomovaných akademiků o něm ví.
Ke stažení
 Článek ve formátu PDF [75,73 kB]
Článek ve formátu PDF [75,73 kB]