Spektroskopie jednotlivých molekul

Jak asi vypadají ty molekuly? To je otázka, která napadne mnohého zvídavého školáka poté, co se dozví, že se všechno kolem nás skládá z atomů a molekul. A škola mu nejdříve odpoví, že molekuly pod mikroskopem vidět nemůžeme, protože jsou moc malé. S pokračujícím vzděláním uslyší něco o vlnové délce světla a rozlišovací schopnosti optických přístrojů, která je omezena difrakčním limitem, což znamená, že nemůžeme vidět předměty menší, než je polovina vlnové délky světla. Co se na tom dá změnit? Nic, samozřejmě. Přesto dnešní fyzika nabízí řešení, která difrakční zákon trochu obcházejí. Jaká?

Na molekuly si posvítíme!

Jedním z řešení je spektroskopie. Jak víme ze základů kvantové mechaniky, atomy a molekuly mají energetické hladiny, které jsou obsazeny elektrony. Při přechodech elektronů mezi různými hladinami je vyzařováno nebo pohlcováno světlo. A protože energetické hladiny jsou „ostré“, mělo by i vyzářené nebo pohlcené světlo mít jen jednu barvu, tedy mělo by být monochromatické. Měříme-li spektrum, monochromatické světlo se projeví jako úzká čára. Ovšem zkusíme-li změřit spektrum třeba roztoku molekul při pokojové teplotě, nikdy úzké čáry neuvidíme. Co naměříme, budou jen široké spektrální pásy. Proč tomu tak je?

Příčin je několik. Jednak molekul je v takovém roztoku zpravidla hodně a světlo vyzářené každou z nich se navzájem překrývá. Navíc, molekuly jsou v neustálém rychlém pohybu. Přesunují se z místa na místo, otáčejí se a vibrují a veškeré tyto pohyby úzkou čáru jakoby „rozmazávají“. Co kdybychom tedy ten roztok zkusili zmrazit? Potom se opravdu otáčivý pohyb a chaotický přesun molekul zastaví, a snížíme-li teplotu až k hranicím teploty kapalného helia, „zamrzne“ i většina vibrací molekul. Pak už každému přechodu elektronu mezi dvěma hladinami molekuly bude odpovídat úzká spektrální čára. Pořád je ale problém v tom, že máme ve zmrzlém roztoku obrovské množství molekul a každá z nich „zamrzla“ trochu jiným způsobem, to znamená, že každá má trochu jiné energetické hladiny, a tudíž i trochu odlišné spektrální čáry. Změříme-li spektrum takového vzorku, uvidíme zase jen široký pás, protože všechny čáry od jednotlivých molekul se navzájem překrývají.

Tady se nabízí otázka: Nemohli bychom zařídit, aby roztok zmrzl tak, že by na tom byly všechny molekuly stejně? Třeba vypěstovat monokrystal? Pak by nám překrývání čar nemuselo vadit, protože by byly všechny stejné. Ukazuje se, že i při sebepečlivější přípravě krystalu je výsledný spektrální pás sice užší, pořád ale mnohonásobně širší, než je čára jedné molekuly.

Chceme-li tedy opravdu vidět, jak vypadá čára od jedné molekuly, zbývá to nejprostší řešení – musíme dostatečně zmenšit počet molekul ve vzorku. Jak se při zmenšování počtu molekul bude měnit tvar spektrálního pásu, ukazuje jednoduchá počítačová simulace na obr. obrázek. Máme-li ve vzorku 10⁵ molekul,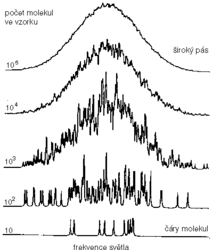 dostáváme už zmíněný široký pás, často nazývaný nehomogenně rozšířený pás. Snížíme-li počet molekul na 10³, pás zůstává široký a objevuje se navíc něco, co asi zná každý spektroskopista – velmi ošklivý šum. Ale pozor, tady nejde o klasický šum. Tomu, co pozorujeme, se někdy říká jemná statistická struktura – ta má původ v různých počtech molekul na jednotlivých frekvencích spektra a je reprodukovatelná! Všimněme si také, že na okrajích spektrálního pásu už dokážeme rozlišit čáry od jednotlivých molekul. Konečně, když dojdeme k počtu 10 molekul ve vzorku, napočítáme ve spektru 10 dobře rozlišených spektrálních čar.

Všechno tedy vypadá jednoduše. Stačí, když vzorek pořádně rozředíme, a můžeme měřit jednotlivé molekuly. Zkusme odhadnout, co znamená vzorek dostatečně rozředit. Jak už víme, potřebujeme mít ve vzorku řádově jen stovky až tisíce molekul. Kdybychom vzali kyvetu o objemu tisíciny mililitru, vyjde nám, že bychom potřebovali koncentraci přibližně 10^–15 mol/l. Jinými slovy, měli bychom rozpouštět desetiny miligramu látky v milionech hektolitrů rozpouštědla. To je, uznejme, trochu nepraktické. Nezbývá, než se nějak pokusit zmenšit objem vzorku. Tady nám pomůže, že z celého vzorku nás zajímá jen ta část, která bude ozářena měřícím laserovým světlem, a tu můžeme snadno zmenšit tak, že před vzorek umístíme malý otvor o průměru několika mikrometrů, nebo tak, že laser na mikrometrový průměr zaostříme. Tím se nám podaří zvýšit požadovanou koncentraci až na 10^–7 mol/l, tedy na docela rozumně dosažitelnou hodnotu.

Jaké molekuly můžeme pozorovat

Pořád nás ale mohou pronásledovat pochybnosti. Bude vůbec světlo vyzářené jednou molekulou dost silné na to, abychom ho dokázali zaregistrovat? V každém případě musíme světlo zachytit co nejúčinněji – nejlépe tak, že vzorek umístíme do ohniska optické soustavy s vysokou numerickou aperturou, jako je parabolické zrcadlo nebo objektiv mikroskopu. Dále musíme použít co nejcitlivější detektor světla, nejlépe fotonásobič a čítač fotonů. I tak ale zaregistrujeme přinejlepším několik procent vyzářeného světla. A vzhledem k tomu, že na výstupu z detektoru bychom potřebovali detegovat aspoň stovky impulzů za sekundu, abychom světlo molekuly odlišili od pozadí, musí být molekula schopna vyzářit za stejnou dobu desetitisíce (10⁴) fotonů, aniž by při tom prodělala jakoukoli změnu. A aby pozadí bylo co nejnižší, musí molekula měřící laserové světlo také účinně pohlcovat. Z toho všeho se nám pomalu rýsují vlastnosti, jaké bude muset molekula mít: vysoký absorpční průřez, vysoký kvantový výtěžek fluorescence, vysokou stabilitu a zanedbatelné obsazování tripletního stavu. To jsou poměrně přísné požadavky, které doposud splňuje několik málo aromatických uhlovodíků. Nejčastěji se pro spektroskopii používají pentacen a terrylen.

Zkusme tedy shrnout experimentální podmínky: potřebujeme měřit zředěný roztok (o koncentraci nejvýše 10^–7 mol/l) vhodně vybraných molekul při nízké teplotě (nejlépe pod 2 K). Signál musíme sbírat optikou s vysokou numerickou aperturou a detegovat velmi citlivým detektorem. A potřebujeme měřit excitační spektra, tzn. budeme sledovat, jakou frekvenci má světlo, které molekula pohltí, tím, že budeme registrovat světlo, které molekula po pohlcení vyzáří.

Jak bude vše vypadat ve skutečnosti?

Vezměme organickou látku terrylen a rozpusťme ji v normálním alkanu na koncentraci 10^–7 mol/l. Normální alkany jsou molekuly s dlouhým uhlíkovým řetězcem, a zvolíme-li délku řetězce tak, že bude přibližně odpovídat délce molekuly terrylenu, máme šanci, že po zmrazení se molekuly dobře zabudují do vzniklého organického krystalu. Dobrou volbou může být třeba dodekan, alkan s deseti uhlíky v řetězci. Na obr.obrázek můžeme vidět spektrum takového vzorku, které na první pohled vypadá spíš jako chaotický šum. Všimněme si ale, že ve skutečnosti jde o dvě různá spektra měřená hned po sobě, která se téměř dokonale překrývají. Podíváme-li se na obr. obrázek, připomene nám to prostřední spektrum – ano, jde o jemnou statistickou strukturu. Přestože jsme zvolili dobrý krystal, molekuly v něm zamrzly chaoticky, a výsledkem je značně rozdílný počet molekul na jednotlivých frekvencích. To je samo o sobě zajímavé, naším cílem ale jsou čáry jednotlivých molekul. Přelaďme tedy frekvenci světla laseru na okraj širokého pásu – tam bychom, jak vidíme na prostředním spektru na obr. obrázek, mohli jednotlivé čáry rozlišit. Jak to dopadlo, vidíme na obr. obrázek. 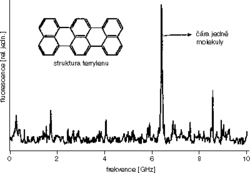Celému spektru dominuje jedna úzká intenzivní čára, která pochází od jedné molekuly. Jak si můžeme být jisti, že jen od jedné molekuly a ne od několika? K tomu se dostaneme později, pro tuto chvíli věřme, že tomu tak je.

Podívejme se dál na obr. obrázek. Tady jsou dvě spektra a hned celá série čar jednotlivých molekul, přitom každá z nich je jinak intenzivní. Proč? Jednou z příčin je, že ne všechny molekuly se nalézají přímo v bodě největšího zaostření laserového světla, jinými slovy některé molekuly jsou ozařovány silněji než jiné. Další příčinou je, že laserové světlo je polarizované. Polarizované světlo nejlépe pohlcují molekuly, které jsou orientovány (přesněji řečeno, jejichž dipólové momenty přechodu jsou orientovány) rovnoběžně s rovinou polarizace laserového světla. Naopak molekuly, které jsou orientovány kolmo k této rovině, nepohlcují světlo vůbec, a takové molekuly ve spektru vůbec neuvidíme. Při měření spekter na obr. obrázek jsme navíc použili tzv. analyzátor. Ten nám umožňuje zjistit, jak je polarizované světlo, které molekuly vyzařují. Opět nejlépe zaregistrujeme molekuly, jejichž vyzářené světlo je polarizované rovnoběžně s rovinou analyzátoru, kdežto ty, jejichž rovina polarizace je kolmá k analyzátoru, nezaregistrujeme vůbec. Podívejme se teď znovu na obr. obrázek. Spektra se liší tím, že jedno (to horní) je změřeno s analyzátorem rovnoběžným s rovinou polarizace laseru, druhé (dolní) s analyzátorem pootočeným kolmo k polarizaci laseru. Všimněme si pozorně, jak se mění intenzity jednotlivých čar. Čáry číslo 1 a 3 jsou v dolním spektru méně než poloviční, čára 2 zmizela úplně a čára 4 zůstala stejná. Co nám to říká o orientaci molekul? Zamyslíme-li se nad tím, molekula 2 musí být rovnoběžná s rovinou polarizace laseru, molekula 4 s ní svírá úhel přibližně 45 stupňů, a molekuly 1 a 3 úhly mezi 0 a 45 stupni. Abychom zjistili přesněji jaké, museli bychom provést více měření. V každém případě nám obr. obrázek ukazuje jednu z možností této metody – dokážeme poměrně přesně měřit orientaci jednotlivých molekul ve vzorku!

Pojďme zase o kousek dál a podívejme se na obr. obrázek. Tady máme detailně změřenou čáru jedné molekuly. Když budeme studovat její tvar, zjistíme, že má tzv. lorentzovský profil. To nám samozřejmě musí udělat radost, protože je to přesně to, co předpovídá kvantová teorie, a je to také jeden z argumentů, proč jde právě o jednu molekulu a ne o více. Když už máme čáru takhle pěkně změřenou, můžeme také odečíst její šířku – ta na obr. 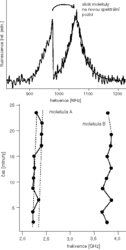má šířku 52 MHz. Tady se znovu obrátíme ke kvantové teorii, jejíž princip neurčitosti nám říká, že šířka čáry je nepřímo úměrná době života vybuzeného stavu molekuly, tedy době, po kterou v sobě molekula „udrží“ pohlcené světlo, než ho znovu vyzáří. Doba života vybuzeného stavu se dá přímo změřit a pro terrylen vychází 3,8 ns, a měla by být pro všechny molekuly stejná. Z toho pak snadno spočítáme, že všechny molekuly by měly mít stejné spektrální čáry o šířce 42 MHz. Ve skutečnosti je to jinak. Na obr. 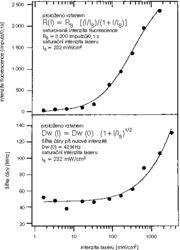je výsledek měření šířek 120 různých molekul. Histogram nám ukazuje, s jakou pravděpodobností se ve spektrech vyskytly čáry s danou šířkou. Vidíme, že oproti očekávání byla většina čar širších než 42 MHz. Čím to bude? Jediné vysvětlení (tedy kromě toho, že kvantová teorie neplatí) je, že během měření spektra se krystal nepatrně mění, že je v neustálém pohybu. To je skutečně překvapující, uvědomíme-li si, že měříme při teplotách 1,6 stupně nad absolutní nulou! Neustálé nepatrné změny struktury krystalu ovlivňují samozřejmě energetické hladiny molekul, a tedy i frekvenci vyzářeného světla, a pokud tyto změny nastávají podstatně rychleji, než dokážeme změřit čáru, měříme vlastně jakousi obálku různě pozměněných čar. Histogramy, jako ten na obr. , nám pak mohou říci hodně o dynamice krystalů, ale i skel nebo polymerů za nízkých teplot.

Struktura krystalu se mění

To, že se struktura krystalu skutečně mění, dokážeme ještě jiným experimentem. Na obr. obrázek nahoře jsme znovu měřili čáru jedné molekuly, ale během měření čára najednou zmizela a objevila se o kousek dál na vyšší frekvenci. Mimochodem, tady máme další argument pro to, že pozorujeme čáru skutečně od jediné molekuly – čára zmizela najednou, v jednom kroku. Jak si vysvětlit tento spektrální „skok“? Pravděpodobně větší změnou krystalu v bezprostřední blízkosti měřené molekuly, jejímž výsledkem je náhlá větší změna energetických hladin molekuly a skok na novou spektrální pozici. Podívejme se na tento jev trochu blíže ve spodním rámečku obr. obrázek. Tady jsme opakovaně měřili spektra dvou molekul A a B a vynesli jsme do grafu, jak se v čase mění poloha maxima jejich čar. Na první pohled vidíme, že každá molekula se chová trochu jinak. Molekula A „přeskakuje“ tam a zpět mezi dvěma definovanými polohami, zatímco molekula B „skáče“ spíše chaoticky. Příčinu možná už uhádneme: krystal se v okolí molekuly A mění tak, že jsou možné pouze dvě konfigurace. Přímo pozorujeme něco, čemu se v teorii skel říká dvouhladinový systém. V případě molekuly B je v jejím nejbližším okolí takových dvouhladinových systémů pravděpodobně více a pohybují se nezávisle na sobě. Dodejme, že oběma jevům, tj. rozšiřování čáry a spektrálním skokům, se ve spektroskopii říká spektrální difuze.

Přidejme ještě jeden argument pro to, že opravdu pozorujeme jednotlivé molekuly. Na obr. obrázek vidíme, jak se parametry čáry, tedy její intenzita a šířka, mění s rostoucí intenzitou laserového světla. Intenzita čáry nejprve mírně, a potom prudčeji roste, ale od určité hodnoty se jakoby začíná nasycovat. Souvisí to s už zmíněnou dobou života vzbuzeného stavu, označme ji t. Když ozařujeme molekulu laserovým světlem, molekula nejprve světlo pohltí, po čase t opět vyzáří a je znovu připravena světlo pohltit. Tento cyklus se během měření mnohokrát opakuje. Zvýšíme-li intenzitu laseru, molekula bude častěji pohlcovat světlo a častěji je také vyzáří, a intenzita její čáry poroste. Zvýšíme-li intenzitu ještě více, můžeme dospět k situaci, že molekula už častěji světlo pohlcovat nemůže, protože musí po dobu t zůstat ve vybuzeném stavu – jinými slovy, během jedné sekundy ji můžeme vybudit pouze 1/t krát. Proto tedy od určité hodnoty intenzity laseru je intenzita čáry nasycena – molekula nemůže vyzářit více světla, protože ho ani nemůže více pohltit. Šířka čáry se rovněž zvětšuje s rostoucí intenzitou – proč, to už bohužel nejde vysvětlit tak názorně. Budeme se muset spokojit s tím, že tento jev, stejně jako nasycování intezity čáry, jsou velmi dobře popsány kvantovou teorií, která uvažuje přechody elektronů mezi dvěma hladinami jedné molekuly. Oba experimenty nám tedy znovu potvrzují, že měříme právě jednu molekulu.

Trochu z historie i budoucnosti

Spektroskopie jednotlivých molekul nemá dlouhou historii. Jemnou statistickou strukturu pozoroval poprvé koncem 80. let W. E. Moerner z IBM a první čáry jednotlivých molekul naměřil M. Orrit z Bordeaux r. 1990. Od doby prvních experimentů je vidět značný pokrok. Kromě jevů nastíněných v tomto článku bylo pozorováno např. shlukování a „anti-shlukování“ fotonů. Jde o časové výpadky ve fluorescenci způsobené tím, že molekula nemůže vyzařovat světlo v době, kdy se nachází v tripletním nebo základním stavu. To jsou příklady jevů, jež není možné měřit na souboru více molekul. Dále jsou k dispozici výsledky řady experimentů optické magnetické rezonance na jednotlivých molekulách, byl měřen stejnosměrný a střídavý Starkův jev, vliv vnějšího tlaku na spektra molekul, vibračně rozlišená fluorescence aj. Nabízí se i otázka, má to všechno nějaký praktický význam? Pokušení odpovědět, že žádný, je pochopitelně veliké, přesto, kromě toho, že může jít o velmi citlivý nástroj pro studium pevných látek, nám určitou naději na praktickou aplikaci dává obr. obrázek. Pokud by se nám povedlo připravit takový materiál, kde by molekula přeskakovala mezi několika definovanými pozicemi tehdy, když budeme chtít, vyrobili bychom spínač na molekulární úrovni! Stejným směrem by vedla cesta i k molekulární paměti.

Přesto se zdá, že kapitola spektroskopie jednotlivých molekul při nízké teplotě se pomalu uzavírá, a budoucnost budou mít metody mikroskopie a spektroskopie jednotlivých molekul při pokojové teplotě. Tento obor se v současnosti velmi rychle rozvíjí díky použití konfokální mikroskopie a skanovací mikroskopie v blízkém poli (Vesmír 74, 236, 1995/4), a zejména aplikace v chemii a biologii vypadají nesmírně nadějně. Ale o tom snad někdy příště.