Můžeme slyšet tvar bubnu?
| 6. 12. 1995Většina pozorování a měření se děje ve vědě nepřímo. Astronomové nemají k dispozici vzorky hvězd, a tak analyzují spektrogramy, geofyzici nemohou podniknout cestu do nitra Země, a tak ‘poslouchají’ seizmogramy. Lékaři používají rentgenů, sonografů a tomografů. Nakolik si však můžeme být jisti, že nám tato nepřímá měření podávají ‘skutečný’ obraz toho, co se měřit domníváme? Můžeme si být jisti, že i v případě, kdy máme nekonečně mnoho měření s nekonečnou přesností, můžeme na jejich základě jednoznačně rekonstruovat měřený objekt? A ještě jinak: nemohly by být dva odlišné objekty, pro něž by i nekonečně mnoho měření s nekonečnou přesností dávalo tytéž výsledky? Tomuto problému rekonstrukce objektu z měření se říká inverzní problém. Podíváme se zde na jeden zvláštní případ tohoto problému: můžeme slyšet tvar bubnu?
Je to otázka matematická a velmi stará. Patří do oblasti zvané izospektrální geometrie. Napřed si ale musíme říci, co budeme rozumět (matematickým) bubnem: to je prostě oblast v rovině, která má vnitřek (to je membrána bubnu) a hranici (okraj), kde je membrána pevně uchycena. Příklady takových útvarů jsou kruh, čtverec, trojúhelník, mnohoúhelník nebo prostě nějaká skvrna s hladkým okrajem. To uchycení membrány bubnu na okraji (říká se tomu nulové okrajové podmínky) je podstatné, jinak by buben mohl vydávat jakýkoli zvuk. Kmitá jen vnitřek bubnu, okraj nikoli, ale je to okraj, který jedině rozhoduje o tom, jaké kmitočty budou slyšet. Matematika ukazuje, že z jedné strany je to jasné: známe-li tvar bubnu (jeho okraj), pak jsou kmitočty jednoznačně určeny řešením vlnové rovnice. Naše otázka je ale obrácená: známe-li naprosto přesně všechny kmitočty, můžeme pak určit jednoznačně tvar bubnu?
V roce 1911 dokázal znamenitý německý matematik Hermann Weyl, že můžeme slyšet velikost (plošný obsah) bubnu. To odpovídá dobře naší zkušenosti, protože čím větší buben, tím hlubší zvuk. O několik let později dokázal švédský matematik Ake Pleijel, že můžeme slyšet i délku okraje bubnu. A americký matematik polského původu Mark Kac vyslovil někdy v šedesátých letech domněnku, že můžeme slyšet i počet ‘děr’ v bubnu. (Představte si třeba kruhový buben s vyříznutým středem ve tvaru dalšího kruhu: membrána kruhu je ovšem pevně přichycena nejen na vnějším, nýbrž i na vnitřním kruhu – to by byl buben s jednou dírou.) Tato domněnka se ukázala být správnou, což dokázali I. M. Singer a Henry McKean.
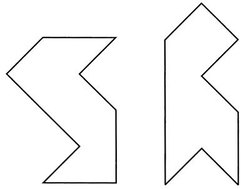Zůstával však stále otevřený problém: můžeme určit tvar bubnu? Dosažené výsledky se zdály naznačovat, že by zvuk mohl obsahovat dostatek geometrické informace k určení tvaru. V roce 1964 se však vyskytlo první mírné varování. John Milnor našel dva ‘bubny’ odlišného tvaru, které zněly naprosto stejně, byly izospektrální. Potíž byla v tom, že to nebyly bubny obyčejné, rovinné, dvourozměrné, nýbrž šestnáctirozměrné. Naděje ale zůstávala, v rovině by to mohlo vypadat všechno jinak. Na Milnora navázali další matematici, kteří zkonstruovali mnoho dalších izospektrálních ‘bubnů’, i méně dimenzionálních. Byly to však příklady dost izolované, chyběla nějaká jednotící idea.
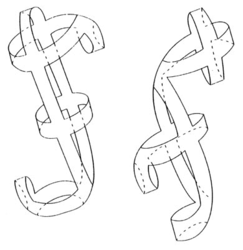
Až r. 1984 Japonec Toshikazu Sunada vymyslel metodu systematické konstrukce izospektrálních bubnů, mezi nimiž byly už i takové, jejichž model se dal vystřihnout a slepit z papíru. Rozhodující příklad sestrojil Peter Buser z Lausannské techniky. Nebyly to sice bubny rovinné, spíše to byly ‘zvony’, ale konečně zde bylo něco názorného. Stejně znějící ‘bubny – zvony’ Petera Busera jsou na obrázku.
Roku 1991 ukazovala Carolyne Gordonová na geometrické konferenci na Dukeově univerzitě tyto Buserovy modely a tehdy napadlo Scotta Wolperta z Marylandské univerzity, že by se rovinný model mohl získat prostě ‘splácnutím’ Buserových modelů. Kupodivu se ukázal tento tak prostý nápad být správný, jenže obtížné to bylo dokázat. I tak to bylo příliš složité na to, aby bylo možno zvuk těchto bubnů přesně vypočítat a srovnat. Mezitím ale Pierre Berard z Univerzity v Grenoblu zobecnil Sunadovu metodu konstrukce bubnů a zavedl klíčový pojem ‘transplantace’ řešení vlnové rovnice z jednoho útvaru na druhý. A to bylo přesně to, co Američané potřebovali. David Webb a Carolyne Gordonová celé dny stříhali a lepili, ale bezvýsledně. Nakonec se vrátili k původnímu ‘splácnutí’ Buserových zvonů. Spojili se s Berardem a Buserem, telefonovali, faxovali, použili složité matematické teorie, až nakonec sestrojili izospektrální dvojici rovinných útvarů, bubnů. A nejen to: důkaz nakonec zjednodušili tak, že se jeho schéma vešlo na trička jejich univerzity. Odpověď na prastarý problém zněla tedy: ne, tvar bubnu nelze slyšet. Jedna dvojice izospektrálních bubnů je na obrázku.
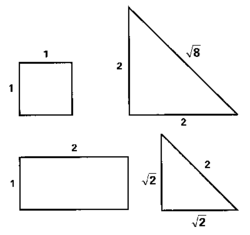Jon Chapman ze Stanfordu pak stříhal dál a našel stejně znějící dvojici ‘dvojbubnů’; najdete je na obrázku. První dvojice zní dohromady stejně jako dvojice druhá. V tomto případu jsou tvary tak jednoduché, že lze vypočítat přesně zvuk, který vydávají.
Touto zápornou odpovědí se ovšem historie Kacova problému neuzavřela, naopak se vyrojilo množství dalších problémů. Tak třeba: existuje trojice stejně znějících bubnů? Nebo: je známo, že ne všechny bubny mají dvojníky, například kruhový buben je jedinečný, není žádný jiný buben, který by zněl stejně. Takže: které bubny jsou takto jedinečné? 1)
Poznámky
Dodatek
/pro čtenáře, kteří mají více času, chuti i trpělivosti/
Naznačil jsem, že výsledný důkaz toho, že bubny na obrázku jsou izospektrální, je jednoduchý a krátký. Pokusím se naznačit jeho ideu; uvidíme přitom také v chodu ‘transplantaci’. Nejprve oba bubny rozdělíme na trojúhelníky (viz obrázek).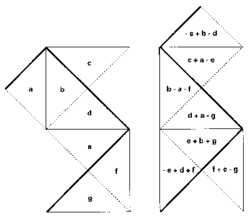 
Ty jsou všechny geometricky shodné a samozřejmě jich je i stejný počet (víme přece už, že plocha a obvod obou bubnů musí být stejné). Rozezníme-li první buben, bude jeho membrána vibrovat a vibrovat bude i každý trojúhelník. Samozřejmě tak, že na okraji nic nevibruje a na přechodech mezi trojúhelníky jsou vibrace stejné. Jde o to, jak přenést toto kmitání na druhý buben, jak je ‘transplantovat’. To se udělá tak, že první buben rozstříháme na jednotlivé trojúhelníky (představujte si, že stále kmitají) a pokusíme se je nějak poskládat do tvaru druhého bubnu, nikoli však pouhým přeuspořádáním, nýbrž tak, že vždy složíme tři původní trojúhelníky v jeden (jejich kmity sečteme). Způsob kombinování je jednak vyznačen tlustými, čárkovanými a jednoduchými stranami (to nám ukazuje, jak máme trojúhelník otočit v rovině nebo vyzvednout a obrátit na záda) a dále ‘vzorečky’, které říkají, jak se kmity mají sečítat. Minus také říká, že trojúhelník musíme nejprve obrátit na záda. První část důkazu spočívá v ověření, že se skutečně strany při těchto kombinacích shodují. Druhý krok pak v ověření, že na okraji nejsou vibrace. Vezměme například horní trojúhelník druhého bubnu, který je složen z trojúhelníků podle vzorce -c+b-d, a podívejme se nejprve na tlustý okraj. V původním bubnu trojúhelníky c a b kmitaly podle tlusté strany shodně, když tedy kmity odečteme, dostaneme nulu. V původním trojúhelníku a byla tlustá strana okrajem, takže nekmitala. Podobně to dokážeme i pro čárkovanou stranu a stejným způsobem pokračujeme dál, trojúhelník po trojúhelníku. A poslední, třetí krok důkazu spočívá v ověření, že uvnitř bubnu na sebe kmitající trojúhelníky navazují hladce. Vezměme zase jako příklad dva horní trojúhelníky druhého bubnu. c na hranici nekmitalo ani v původním bubnu, takže na něm nezáleží. a a b kmitaly shodně, podobně i b a d. Podobně pro všechny ostatní trojúhelníky. To, že vydávají stejný zvuk, vyplývá pak jednak z jednoznačnosti řešení vlnové rovnice a dále pak z toho, že kmity druhého bubnu se získaly transplantací řešení pro první buben.
O autorovi
Jiří Fiala
Doporučujeme
Se štírem na štíru
Ustrašená společnost 
