Statistiky chtějí opatrnost

Známé a často citované úsloví označuje statistiku za třetí, nejvyšší, stupeň lži (pravda, podle některých autorů bojuje o prvenství s předpovědí počasí) a dost lidí se na ni dívá s odpovídající nedůvěrou. Pro mnohé jiné je ale tvrzení podepřené statistickými údaji nezvratné a nezpochybnitelné – čísla jsou vždy jednoznačná. Jak tomu je ve skutečnosti? Může statistika vůbec lhát? Samozřejmě že může. Lhát může literatura, film, dokonce i dokumentární fotografie (a nemusí být ani retušovaná) - stačí s ní jen „správně“ zacházet. Tak proč by právě statistika měla být výjimkou. V následujících odstavcích se zmíníme o hlavních principech statistické lži a pokusíme se naznačit i základní metody sebeobrany proti ní.

Úvodem bychom si snad měli vyjasnit jednu věc. Statistika je nástroj, a to nástroj značně účinný. Při zodpovědném zacházení poskytuje nedocenitelné a jinak nezískatelné rozbory kvantitativní stránky světa. V tomto smyslu je její autorita hodně zasloužená. Lhát může jenom tehdy, je-li použita deformovaně - ať už jde o záměr, nebo o nepochopení. Možných způsobů zneužití statistiky je mnoho, vcelku ale mohou být roztříděny do tří kategorií.

Kategorie 1: Hrubá lež

Jde o nejprimitivnější typ statistického lhaní a svou podstatou do statistiky vlastně ani nepatří. Spočívá v tom, že je statistická forma sdělování užita k šíření údajů od počátku vylhaných – nesprávných čísel, nepravdivých tabulek, nesmyslných grafů. Ve společnosti bez demokratických zpětných vazeb je věcně nenapadnutelná, pokud slouží vládnoucí moci. Proto v takové společnosti ani neexistuje potřeba sahat k subtilnějším metodám statistického klamání. My se jí ale nebudeme dále zabývat - je to prostě lež jako každá jiná a se statistikou má společné jen vnější výrazové prostředky.

Kategorie 2: Odpovědi na jiné otázky

Dosti častým a snad nejúčinněji využívaným způsobem, jak klamat pomocí statistiky, je používání metod nepřiměřených danému problému.

Při tomto postupu jsou výsledky získané jinak korektními procedurami nesprávně interpretovány. Nebo, což je totéž z jiné strany, při hledání odpovědí na položené otázky jsou použity postupy, které vlastně odpovídají na otázky trochu jiné. Tato strategie má mnoho různých podob. Místo obecných charakteristik snad lépe poslouží několik příkladů.

Oblíbenou pomůckou pro statistické klamání jsou manipulace s průměrem. Záměna pojmů „průměrný“ a “nejobvyklejší“ (odůvodnitelná u statistických znaků s Gaussovým rozložením hodnot, ale jinak scestná) je poměrně častá. Tvoří podstatu třeba i známého žertu o dvou pánech, z nichž jeden snědl dvě kuřata a druhý žádné, takže v průměru se oba dobře najedli. Žaludek toho hladového dobře ví, že průměr ze dvou hodnot zdaleka není všeobecně platná hodnota. Něco podobného, i když méně nápadně, představuje tak oblíbené průměry známek ve školní klasifikaci. Má-li žák průměr z pěti známek 1,8, pak už sama záměna slov „průměr známek“ za „průměrná známka“ zavádí (známka 1,8 ani neexistuje) a zdaleka už neznamená „typická známka“. Vždyť tento průměr může reprezentovat známky 1, 1, 1, 1, 5 nebo 2, 2, 2, 2, 1 nebo 1, 3, 1, 3, 1, a vždy jde o zcela jiný obraz žáka (typického jedničkáře nebo dvojkaře s ojedinělým výkyvem, či žáka s rozkolísanými výkony). V zásadě průměr sám o sobě, jakkoli je jistě užitečnou charakteristikou polohy, vypovídá o typické hodnotě poměrně málo.

Jiný trik s průměrem je v zaměňování základních souborů, ve kterých se průměr počítá. Pamětníci časů předminulých si asi vzpomenou na doby, kdy se zvyšování cen cudně nazývalo zaokrouhlování. Stalo se tehdy, že jakési zboží se vyskytovalo ve dvou variantách, které stály řekněme 46 a 56 Kčs (čísla jsou vymyšlená – autorova paměť není absolutní). Po úpravě bylo zboží prodáváno za jednotnou cenu 50 Kčs a tisk neopomněl zdůraznit, že si spotřebitelé polepšili, protože průměrná cena by byla 51 Kčs. Průměr obou cen by skutečně takový byl, ale aby si spotřebitelé polepšili, musely by se snížit průměrné platby za toto zboží v obchodech. A to už je jiný základní soubor, ve kterém může být každý druh zastoupen v jiném poměru. Pokud se levnějšího provedení prodávalo, řekněme, 3krát více než dražšího, pak se průměrná platba zvýšila ze 48,50 na 50 Kčs, neboť

((3 x 46) + (1 x 56)) : 4 = 48,50.

Jiný, ještě půvabnější příklad odvážné manipulace se základními soubory se udál v dobách už pouze minulých. Při politickém školení o morální a jiné náročnosti lékařské práce uvedl lektor i statistické údaje. Konkrétně: průměrný věk obyvatelstva je asi 70 let, průměrný věk lékařů je 42 let – tak vyčerpávající je zodpovědná práce lékaře. (Mimochodem – auditorium tvořil zdravotnický personál, tedy lidé, kteří věděli, že lékař zkolabovavší ve čtyřiceti z přepracování není tak obvyklý jev. Přesto prý „přesné statistické údaje“ přijali jako pádný argument. Taková je síla statistiky!) A nejlepší na věci je, že ten lektor ani tak moc nelhal, pokud jde o čísla. Jen zaměnil průměrný věk dožití (tedy věk, ve kterém lidé umírají) a průměrný momentální věk žijících lékařů podle evidence ministerstva zdravotnictví.

Snad ještě oblíbenějším a tvárnějším nástrojem na matení mysli jsou procenta. Zvýšení roční výroby traktorů ze 2 kusů na 10 je zvýšení o 8 kusů, ale o 400 %. Podobné zvýšení ze 100 kusů na 140 kusů je sice o 40 kusů (5krát větší), ale jen o 40 % (10krát menší). Střední generace je, díky školním učebnicím a jejich pasážím o úspěších socialistického tábora, poměrně dobře trénovaná v sebeobraně proti takovým manipulacím. Snad. V zásadě by měl zodpovědný příjemce informací považovat za velmi podezřelé všechny procentové údaje nedoplněné o absolutní čísla.

Méně průhledné, ale o to nebezpečnější jsou triky okolo statistické indukce, tedy okolí zobecňování údajů zjištěných u části souboru na celý soubor. Nepřiměřenost položené otázky a dat užitých k jejímu zodpovězení se tam může dobře uplatnit. Průzkumy veřejného mínění například mohou někdy poskytovat dost názorných ukázek; ale nejen ony. Jistě jste už slyšeli, že alkohol za volantem je nebezpečný, protože je, statisticky, nejčastější příčinou nehod.

Aby bylo jasno, i autor je přesvědčen, že alkohol za volant nepatří a že zaviňuje mnoho (asi nejvíce) nehod. To ale vůbec neplyne z údaje, že se podílel na 40 % (řekněme) nehod a ostatní příčiny byly zastoupeny méně. Odmysleme si teď skutečnost, že i klasifikace příčin nemusí být vždy jasná a že i opilý řidič může havarovat ze zcela jiného důvodu. Výše uvedený procentuální argument lze snadno zobecnit. Například se dá soudit, že většina nehod byla způsobena řidiči s hnědými vlasy – pak ale hnědé vlasy za volant také nepatří. Snad všichni viníci nehod řídili oblečení. Pryč se šaty za volantem! Aby měl argument se 40 % nehod vinou alkoholu nějakou váhu, museli bychom vědět, že mezi všemi řidiči je méně než 40 % opilých (skoro jistě – snad s výjimkou jižní Moravy v době hodů – je). V opačném případě – kdyby podíl zalkoholizovaných mezi všemi řidiči byl vyšší než 40 %, byl by alkohol vlastně významným prostředkem pro snížení nehodovosti. Kapitolu samu o sobě tvoří

dogmatické lpění na teoretickém modelu.

Hodně statistických znaků nabývá hodnot, jejichž četnosti (a související pravděpodobnosti) jsou rozloženy podle již zmíněné Gaussovy normální křivky (viz rovněž obrázek). Je to křivka zvonovitého tvaru, souměrná podle nejvyšší četnosti (nejčastější hodnoty) a její teoretický model nikde nedosahuje přesně nulové hodnoty, i když k oběma koncům stále klesá.

Gaussovo rozložení uspokojivě popisuje četnosti hodnot řady statistických znaků – třeba tělesné výšky. To ale platí pro celkem běžné hodnoty, nepříliš vzdálené od průměru. Dogmatické lpění na doslovné platnosti teoretického Gaussova modelu by znamenalo, že nenulovou, kladnou (i když jistě velice malou) pravděpodobnost výskytu mají i výšky několik desítek metrů, nebo naopak i výšky záporné.

Před pár lety proběhla tiskem drobná perlička o tom, že v Anglii byl k placení alimentů odsouzen muž, jehož otcovství bylo možné jen v případě asi patnáctiměsíčního těhotenství. Žalobkyně přivedla znalce, kteří potvrdili, že doba těhotenství je statistický znak respektující Gaussovu křivku s průměrem 270 dnů a že Gaussovo rozložení udává pro patnáctiměsíční těhotenství sice malou, ale přeci jen kladnou pravděpodobnost. Nikoho tehdy asi nenapadlo uvést, že s naprosto stejnou pravděpodobností může normální zdravé těhotenství trvat 3 měsíce, popřípadě že podle téže logiky se může dítě s kladnou pravděpodobností narodit dříve, než bylo počato. Každý teoretický model má své meze praktické použitelnosti, jejichž překročení znamená hrubé zkreslení závěrů.

Už o něco méně časté, ale interpretačně o to svůdnější jsou statistické argumenty založené na regresi a korelaci. Regresní metody, zhruba řečeno, umožňují nalézt základní trendy vývoje (zpravidla v časové posloupnosti) číselných řad, a to i tehdy, kdy jsou narušeny značným náhodným šumem. V zásadě platí, že regresní křivka proložená náhodně rozptýlenými body popisuje chování sledovaného procesu pouze v rozsahu toho období, které je získanými body pokryto. Prodloužení regresní křivky za toto rozmezí je možné, ale jen do jisté míry a s jistým stupněm důvěryhodnosti. Současná matematická statistika disponuje metodami, které umožňují onen stupeň odvodit. O ty se ale demagogové nestarají a vesele extrapolují regresní křivky bez omezení. Příklady nám i tentokrát pomohou předchozí obecný výklad názorněji ilustrovat.

V civilizovaných zemích klesá dětská úmrtnost a v jistém období lze tento pokles graficky znázornit klesající přímkou (regresní přímkou proloženou hodnotami dětské úmrtnosti v jednotlivých letech). Je zřejmé, že taková přímka nemůže být libovolně prodloužena. Procento úmrtí prostě nemůže být záporné. V jistém okamžiku se tedy příslušná přímka zalomí v oblouk a časem se zhruba ustálí na nějaké téměř konstantní úrovni. V Británii nastal onen okamžik zlomu v době, kdy začalo hromadné očkování dětí. Odpůrci očkování, příslušníci některých extrémních náboženských sekt, tohoto faktu využili ke „statistickému důkazu“ škodlivosti očkování.

Do jisté míry podobně postupovali futurologové šedesátých let při extrapolaci křivek vzrůstu populace. Ne že by enormní vzrůst populace nebyl skutečnou hrozbou pro budoucnost lidstva. Nicméně i dnes se ukazuje, že prodloužení exponenciálních křivek růstu populace o dvacet let bylo nerealistické a skutečné hodnoty, jakkoli jsou i tak dost hrozivé, se přece jenom vyvíjely pomaleji.

Většina procesů v jistém počátečním stadiu nabývá prudké tempo, jehož mechanické prodloužení do budoucnosti může vést k otřesným závěrům. Kdybychom křivku přírůstku nemocných aidsem na přelomu sedmdesátých a osmdesátých let dostatečně (a ani ne zas tak moc) prodloužili, patrně bychom snadno došli k závěru, že počet nemocných bude za pár desítek let vyšší než počet obyvatel Země. Ani tato poznámka nemá zpochybňovat nebezpečí choroby, ale výhradně dost časté ležérní zacházení se statistickými daty.

S regresí trochu souvisí takzvaná korelace. Vyjadřuje stupeň podobnosti vývoje dvou číselných řad. Korelační koeficient je číslo mezi +1 a -1, které ukazuje, jak moc se dvě číselné řady vyvíjejí shodně (pro koeficient kladný) nebo protichůdně (koeficient záporný). Může leccos odhalit, ale v rukou schopného demagoga také dokáže divy. Při čtení údajů o korelaci dvou procesů nesmíme zapomenout, že korelační koeficient nevyjadřuje nic více než formální podobnost dvou číselných řad. Je-li vysoký, musí nastoupit jiné (už ne jenom jednoduše statistické) rozbory příčin oné formální podobnosti. Ty ukáží, která z obou (nebo i více) řad závisí na vývoji té druhé a která z nich vývoj určuje. Také mohou obě, ač vzájemně nezávislé, odrážet vývoj nějakého dalšího činitele ve statistických datech explicitně neuváděného, a konečně může jít o podobnost vývoje čistě náhodnou.

Např. závislost výskytu rakoviny plic na kouření cigaret byla nejdříve objevena statisticky – zjištěním vysoké korelace časových řad spotřeby cigaret a výskytu uvedeného onemocnění. Určité zpoždění nárůstu nemocných za růstem spotřeby cigaret naznačilo, že rakovina plic nebude patrně příčinou zvýšené chuti na cigaretu, ale naopak. Náročné laboratorní testy potvrdily skutečnou kauzální závislost příčin a následků. Argumenty o karcinogennosti dalších potravin jsou také často založeny na korelačních údajích, i když řada případů se zdá být zpracována mnohem méně přesvědčivě.

Něco jiného je statistiky prokázaná vysoká korelace mezi platy anglikánských kněží a cenami whisky v Anglii. Ne že by pastoři dostávali plat na to, aby měli za co pít. Ani naopak nejsou jistě tak silnými spotřebiteli, aby jejich koupěschopnost diktovala ceny. Obě číselné řady rostou vinou třetího faktoru – inflace. Podobně dlouhodobá korelace mezi spotřebou benzínu a počtem krádeží aut nenaznačuje ani tak spolupráci mezi pumpaři a zloději, jako spíše celkový růst motorizace.

Některé korelace jsou patrně opravdu čistě náhodné – nebo představují výzvu lidské fantazii. V literatuře se někdy např. uvádí údajná vysoká korelace mezi délkou sukní a konjunkturou na burze. Čím vyšší ceny akcií a oživení trhu – tím kratší sukně. Výsledek byl publikován již před lety a autorovi se nepodařilo zjistit, zda byl dalším vývojem potvrzen. V každém případě – vynalézavost vysvětlovatelů se má čím zabývat.

Zdá se, že regrese a korelace představují asi tak horní hranici masově prezentovaných statistických metod, které jsou sice formálně správně provedeny, zhruba i správně popsány adresátovi z nich odvozených argumentů, ale často chybně (ač už omylem nebo účelově) interpretovány a propagačně využívány. Zbývají ale ještě metody třetí kategorie.

Kategorie 3: Dojmologie

Hranice mezi metodami předchozí skupiny a těmi, které připomeneme v této části, je někdy trochu neostrá. V obou případech jde o překroucení nebo posunutí smyslu jinak správných statistických výsledků. Zatímco dosud jsme se zmiňovali o matení pomocí sice zkreslené, ale přece jenom nějaké logiky a rozumových úvah, nyní si řekneme něco o útocích na podvědomí. U statistických argumentů záleží nejen na tom, z jak spolehlivých podkladů byly vyvozeny a jak byly čtenáři vysvětleny, ale i na tom, jakou formou byly prezentovány.

Zkuste si sami, zda na vás následující (věcně rovnocenné) výroky zapůsobí vždy stejně:

„Deficit je 3,8 mld.“

„Deficit je 3 800 milionů.“

„Deficit je 3 800 000 000.“

Tentýž údaj vyzní pokaždé jinak. Stačilo jenom změnit řád jednotek. Dojmu serióznosti se dosahuje uváděním přesných cifer, ať vznikly jakkoli. Sdělení, že názor zastává 57,14 % dotázaných, může také znamenat, že se k němu hlásí čtyři z celkového počtu sedmi respondentů. Překlad z cizojazyčné publikace s údajem o “obvyklé vzdálenosti 91 m 44 cm“ nebo o “nákladech 29 505 000 Kčs“ mohl vzniknout snaživým převodem 100 yardů, popřípadě 1,5 milionu DM, které už zdaleka nedělají dojem takové akurátní přesnosti.

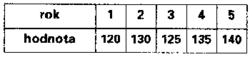
Bohaté možnosti působení na podvědomí nabízí vhodná kombinace údajů a jejich absolutních nebo relativních změn při uvádění časových řad. Představme si údaj (produkci podniku, platy, stupeň znečištění – zkrátka cokoli, co se v čase mění), který v pěti letech po sobě nabyl hodnotu 1 000, 1 100, 1 200, 1 300, 1 400  nějakých jednotek. Tedy viditelně dynamicky roste. Můžeme ale také říci, že ve 2. roce dosáhl 110 % prvního roku, ve 3. roce 109 % druhého roku, ve 4. roce 108,3 % třetího roku a v 5. roce 107,7 % čtvrtého roku. Údaje stále rostou, ale čtenář má pocit zpomalování růstu. Uvedení samotných přírůstků může pocity ještě prohloubit. Absolutní přírůstky oproti předchozímu roku jsou

100, 100, 100, 100

jednotek, takže místo rostoucí řady skutečných hodnot vidí čtenář konstantní („zkostnatělý“, nedynamický, zakonzervovaný) průběh číselné řady. Relativní přírůstky

0,1; 0,9; 0,83; 0,77

dokonce tvoří klesající řadu. Pocit, že to se sledovaným údajem jde nějak s kopce, se u většiny čtenářů bezpečně dostaví. Doménou účelového působení na podvědomí čtenáře statistik jsou ale grafy. Číselné údaje je přece jenom nutné vnímat a alespoň povrchně zpracovat i rozumově. Křivka nebo (což je ještě horší) sled panáčků či krychliček vyvolává pocity přímo.

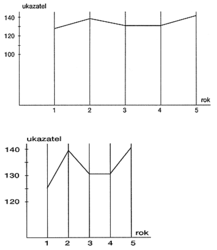
Vývoj údaje popsaného tabulkou může znázornit horní graf, nebo také ve zpracování na grafu dolním. Pocit dynamiky znázorněného vývoje je pokaždé zcela jiný.Také volba mezi lineárním, plošným, nebo iluzivně prostorovým znázorněním je v podstatě volbou pocitu, který má být ve čtenáři vyvolán. Uvědomme si, že zdvojnásobení vypadá v lineárním, plošném a prostorovém zobrazení tak, jak vidíme na obrázku.

Jaká pak je skutečná vypovídací hodnota grafu složeného z řady domečků, panáčků, stromků a podobných kresbiček a jak ale takové malůvky působí na tvorbu podvědomých postojů k zobrazovaným údajům, to si čtenář dokáže posoudit i bez návodu.

Máme tedy věřit statistikám?

Předchozí přehled umožňuje stručné shrnutí. Jak moc máme věřit statistickým údajům, které jsou nám předkládány? Především záleží na tom, za jak spolehlivý považujeme samotný zdroj dat. To je spíše záležitost naší důvěry a konfrontace údajů s předchozí zkušeností, než věc rozboru použitých statistických metod. Teprve poté nastupuje zamyšlení, zda je s jejich výkladem všechno v pořádku. I v tomto případě bude srovnání předkládaných závěrů se zkušeností přinejmenším zajímavou motivací pro hlubší úvahu. Je dobré si především promyslet, zda použitá metodika ladí s proklamovanými cíli rozboru a také zda se v nás někdo nepokouší vyvolat pro něj žádoucí pocity. Snad předchozí odstavce alespoň naznačily, na co si máme dávat pozor především.

Těm, kdo se chtějí o kouzlení se statistikou, seriózním i neseriózním, dozvědět více, doporučujeme zalistovat v knize Helmuta Swobody: Moderní statistika, kterou jako překlad z němčiny vydalo v roce 1977 nakladatelství Svoboda. Je to zajímavé čtení určené nematematikům, ze kterého se čtenář dozví mnoho nejen o záludnostech, ale i o seriózních metodách statistiky. Některé z příkladů uvedených výše mají původ právě ve Swobodově knize. Dalšími příklady nás čas od času zásobuje běžná novinová publicistika.