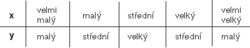Soft computing
Slovní spojení soft computing je nový anglický termín, který nemá stručný a výstižný český překlad, takže se možná v češtině zabydlí podobně jako software, second hand (sekáč) nebo dříve džem a džez. Slovo computing nelze mechanicky překládat jako počítání; jde spíše o výpočetní metody, algoritmy a teorie. Slovo soft může mít i hanlivý význam; z českých ekvivalentů je nejhezčí hebký, ale nečekám, že by se v našem kontextu vžil. 1) Pokusím se vymezit, co se pod pojmem soft computing (SC) skrývá a co od toho můžeme čekat.
Matematika je skvělá; počítače jsou skvělé
Matematika je úžasná svou přesností, rigorózností, jasným rozlišením pravdivých a nepravdivých tvrzení, svou klasickou logikou. Buduje a studuje nádherné struktury čísel, množin, funkcí, matic, vektorů atd. Nabízí optimální řešení velmi široké palety přesně definovaných problémů a často i metody, jak se k optimálnímu řešení libovolně přesně přiblížit. Díky výsledkům informatiky poskytují počítače matematice stále více možností, aby tyto metody numericky uskutečňovala a prakticky aplikovala. Matematika je královnou věd – a počítače jsou její vojsko. Tuto chválu předesílám, aby bylo jasno, že role matematiky a informatiky nebude v článku zpochybňována. Ale přesto:Příliš složité problémy vyžadují nové, „zlidštěné“ výpočetní metody a jisté změny ve způsobu jejich hodnocení
Profesor L. Zadeh, autor teorie fuzzy množin i termínu „soft computing“, zdůrazňuje, že příliš složité či neurčité problémy buď exaktní řešení vylučují, nebo je činí absurdními. Naše poznání reálného světa je plné nepřesnosti, potřebné informace jsou často nedostupné, analyzované systémy nepřesně či neúplně definované (např. v ekonomii, plánování, živých systémech či společenských systémech). Zadeh tomu říká „princip neslučitelnosti“: problémy právě nastíněného typu se neslučují s ideálem exaktního optimálního řešení. Optimální řešení buďto neexistují, nebo jsou nezajímavá či příliš nákladná; je třeba učit se toleranci a hledat řešení, která jsou dostatečně dobrá. Pro jistotu dodávám: To nemá být omluva pro slabé znalosti matematiky; tam, kde optimální řešení existuje a je dostupné a žádoucí, by byl hřích nevyužít i nejmodernější výsledky klasické matematiky. V situacích, které jsme nastínili, je však možno se poučit z toho, jak my lidé přirozeně řešíme řadu problémů dostatečně dobrým způsobem. Zadehův oblíbený příklad je zaparkování auta. Jsou známy přesné (diferenciální) rovnice popisující zcela přesně nejlepší cestu, po níž by mělo vaše auto jet, aby v dané situaci optimálně zaparkovalo. Tuto rovnici ale určitě při parkování nepoužijete; stačí pár přibližných pravidel jako „teď při couvání zahnu hodně doleva“ apod. Rozumným způsobům řešení podobných problémů se ovšem musíme učit a postupně se zlepšovat. Lze se podobně dívat na (některé) výpočetní metody? Uvedeme několik příkladů, byť jen velmi stručně a povrchně; na víc není místo.
Optimální řešení buďto neexistují, nebo jsou nezajímavá či příliš nákladná; je třeba učit se toleranci a hledat řešení, která jsou dostatečně dobrá. Pro jistotu dodávám: To nemá být omluva pro slabé znalosti matematiky; tam, kde optimální řešení existuje a je dostupné a žádoucí, by byl hřích nevyužít i nejmodernější výsledky klasické matematiky. V situacích, které jsme nastínili, je však možno se poučit z toho, jak my lidé přirozeně řešíme řadu problémů dostatečně dobrým způsobem. Zadehův oblíbený příklad je zaparkování auta. Jsou známy přesné (diferenciální) rovnice popisující zcela přesně nejlepší cestu, po níž by mělo vaše auto jet, aby v dané situaci optimálně zaparkovalo. Tuto rovnici ale určitě při parkování nepoužijete; stačí pár přibližných pravidel jako „teď při couvání zahnu hodně doleva“ apod. Rozumným způsobům řešení podobných problémů se ovšem musíme učit a postupně se zlepšovat. Lze se podobně dívat na (některé) výpočetní metody? Uvedeme několik příkladů, byť jen velmi stručně a povrchně; na víc není místo.
Fuzzy počítání
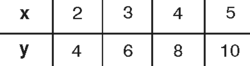
Termín „fuzzy“ (ve spojení „fuzzy množina, fuzzy logika“) je příkladem dalšího anglického termínu, pro který nebyl nalezen vhodný český ekvivalent. Fuzzy podmnožina nějakého oboru (pojem zavedl L. Zadeh r. 1965) je určena tím, že každý prvek toho oboru patří do naší fuzzy podmnožiny v nějakém stupni (což je obvykle reálné číslo mezi nulou a jedničkou). Fuzzy množiny velmi dobře modelují vágní pojmy, jako je např. „vysoká teplota“. Představujeme si, že každé konkrétní hodnotě teploty odpovídá číslo říkající, do jaké míry je tato teplota vysoká. Jak lze s fuzzy množinami, resp. fuzzy pojmy počítat? Představme si nejprve obvyklou funkci danou tabulkou hodnot, třeba tuto:(Naše funkce přiřazuje každému přirozenému číslu od 2 do 5 jeho dvojnásobek.) Nyní si prohlédněme jinou tabulku, v níž se místo čísel vyskytují fuzzy pojmy velmi malý, malý, střední, velký, velmi velký.
Tato tabulka jen velmi neurčitě popisuje nějakou funkci, ale může být velmi přirozeným popisem, který v dané situaci může stačit, a dokonce – známe-li významy uvedených pojmů, tj. jsou-li dány odpovídající fuzzy množiny – lze pomocí takové tabulky (obvykle vyjadřované ve formě pravidel tvaru „když x je velmi malé, pak y je malé″) spočítat přesné hodnoty funkce, která naši informaci vystihne. Toho se podstatně využívá v metodách fuzzy řízení (fuzzy regulace) při formalizaci empirických znalostí o chování řízeného systému.
Neuronové sítě
Popišme jeden důležitý druh neuronových sítí. Jde o to umět počítat hodnoty funkce, která dostatečně dobře odpovídá datům, jež jsou souborem konkrétních příkladů chování této funkce. Taková data si můžeme představit jako velikou tabulku číselných hodnot. Každý řádek tabulky udává hodnoty nezávisle proměnných a jim příslušné hodnoty závisle proměnných. Neuronová síť se skládá z uzlů (neuronů) a hran. Každá hrana vede od nějakého neuronu k jinému neuronu. Některé neurony jsou vstupní – nevede do nich žádná hrana (odpovídají nezávisle proměnným), jiné jsou výstupní – nevede z nich žádná hrana (odpovídají závisle proměnným), ostatní jsou vnitřní. Neuronům i hranám přísluší různé přirozeně popsané charakteristiky, jež určují, jak každý neuron určuje (z hodnot k němu přicházejících po hranách k němu vedoucích) hodnoty, které pak dále posílá po hranách, jež z něj vycházejí. Představte si, že konkrétní hodnoty nezávisle proměnných vstoupí (z okolního prostředí) do vstupních neuronů, síť je zpracovává, a nakonec výstupní neurony vydají hodnoty závisle proměnných. Přejeme si, aby tyto hodnoty byly v dobré shodě s našimi daty. Je pozoruhodné, že pokud tomu tak není, existují metody (algoritmy), pomocí nichž se neuronová síť může učit, tj. postupně měnit své charakteristiky tak, aby se shoda s daty zlepšovala. Jak naznačují užité termíny, tato technika je do jisté míry inspirována neurologií; může na ní být zcela nezávislá, ale naopak ji lze využít např. k matematickému modelování neurologických procesů.
Neuronům i hranám přísluší různé přirozeně popsané charakteristiky, jež určují, jak každý neuron určuje (z hodnot k němu přicházejících po hranách k němu vedoucích) hodnoty, které pak dále posílá po hranách, jež z něj vycházejí. Představte si, že konkrétní hodnoty nezávisle proměnných vstoupí (z okolního prostředí) do vstupních neuronů, síť je zpracovává, a nakonec výstupní neurony vydají hodnoty závisle proměnných. Přejeme si, aby tyto hodnoty byly v dobré shodě s našimi daty. Je pozoruhodné, že pokud tomu tak není, existují metody (algoritmy), pomocí nichž se neuronová síť může učit, tj. postupně měnit své charakteristiky tak, aby se shoda s daty zlepšovala. Jak naznačují užité termíny, tato technika je do jisté míry inspirována neurologií; může na ní být zcela nezávislá, ale naopak ji lze využít např. k matematickému modelování neurologických procesů.
Genetické algoritmy (evoluční počítání)
V jistých případech máme k dispozici řadu různých (lepších a horších) řešení nějakého problému a každé řešení je popsáno řetězcem znaků (genem, chcete-li). Nová řešení se hledají tak, že se už známá řešení obměňují a kombinují navzájem (kříží) podobně jako geny v genetice a ze získaného materiálu se vybírá s ohledem na kvalitu (selekce), čímž vzniká nová populace různých řešení.Pravděpodobnostní počítání
Teorie pravděpodobnosti je jedna z klasických, hluboce rozvinutých matematických teorií a výpočetních metod; chci ale zmínit, že v poslední době vznikly některé alternativy klasické pravděpodobnosti, např. teorie posibilistických měr a Dempsterova-Shaferova teorie domněnkových funkcí, které se hodí v řadě situací, kdy předpoklady klasických pravděpodobnostních metod nejsou splněny nebo nejsou ověřitelné.Těžení z dat
Tento český termín (v angličtině data mining) se docela povedl. Jde o to, že stále častěji vznikají velké soubory dat (v kosmickém výzkumu, ale třeba také při provozu supermarketu), v nichž se může skrývat cenná znalost (třeba o tom, jakým způsobem souvisí věk a pohlaví zákazníka s tím, co kupuje). Cílem je tuto znalost z dat vydobýt. Dnes je tento směr velmi módní; neodpustím si připomenout, že jeho základní myšlenka byla formulována v souvislosti s českou metodou automatické tvorby hypotéz GUHA (General Unary Hypotheses Automation) už r. 1965, což dnes ve světě ví málokdo.Tyto a podobné metody či přístupy lze nejrůzněji kombinovat. Například parametry zadání funkce pomocí fuzzy pravidel (či fuzzy tabulky), tj. detaily významů užitých fuzzy pojmů, mohou být vylepšovány (laděny) pomocí neuronové sítě či genetického algoritmu. Genetický algoritmus může být řízen fuzzy regulátorem. Neuronová síť může být vytvářena genetickým algoritmem a inicializovat ji lze metodou GUHA. Je možno kombinovat fuzzy přístup s pravděpodobnostním (při přísném odlišení toho, co je fuzzy, tj. vágní, a co je pravděpodobnostní, tj. náhodné), dají se vytvářet posibilistické analogie pravděpodobnostních výpočtových metod. A našli bychom řadu dalších příkladů.
Co je soft computing
Citujme L. Zadeha: Soft computing (SC) je spojení výpočtových metodologií, jako jsou zejména fuzzy logika, neuropočítání, genetické počítání a pravděpodobnostní počítání. Metodologie zahrnující soft computing jsou ponejvíce komplementární a synergistické, spíše než konkurenční. Vedoucím principem SC je využití tolerance vůči nepřesnosti, nejistotě, částečné pravdě a aproximaci k dosažení zvládnutelnosti, robustnosti, nižší ceny řešení a lepšího souhlasu s realitou. Jedním z hlavních cílů SC je vytvořit základy pro navrhování, vytváření a aplikování inteligentních systémů uplatňujících své složky symbioticky a ne izolovaně. To je pěkné a dostatečně široké vymezení, které by nemělo být chápáno tak, že SC spočívá prostě v tom, že se dá dohromady fuzzy, neuronové a genetické počítání. Jak upozorňují francouzští odborníci na fuzzy problematiku Didier Dubois a Henri Prade, jde obecně o tvůrčí propojení metod využívajících numerická data a metod pracujících se znalostmi, metod matematického modelování a symbolického usuzování. (To vše pod zorným úhlem vedoucího principu tolerance, který je formulován výše.) Pro jistotu zopakuji ještě jednou: Vůbec nejde o relativizování významu metod klasické matematiky; naopak jde o to, aby byly nalézány účinné výpočtové metody pro situace, kde jsou klasické metody nepoužitelné.
„Svatým posláním“ matematika a informatika zabývajícího se SC je dbát na to, aby i tato disciplína měla tak rigorózní základy, jak jen je možno
Ilustruji to na pojmu fuzzy logika. Stalo se módou nazývat tak veškeré užití fuzzy přístupu. To je (jak opět říká Zadeh) fuzzy logika v širokém smyslu. V úzkém smyslu je možno fuzzy logiku vybudovat jako striktně formální logický systém analogický klasické formální logice, ale s komparativním pojmem pravdy: výroky mohou být srovnávány podle stupně pravdivosti. Jde tedy o druh vícehodnotové logiky, která byla rozvíjena již několik dekád před vznikem fuzzy přístupu; ten však dává vícehodnotové logice zcela novou inspiraci a obráceně přístup vícehodnotové logiky dává fuzzy logice pozoruhodnou hloubku jako skutečné logice.Paradigmata přicházejí a odcházejí; co zůstává?
Dostáváme se k otázce v titulku článku. SC je dnes mladá, ale etablovaná disciplína. Čtvrtým rokem vychází mezinárodní časopis Soft computing (vydává jej Springer Verlag), existují i různé monografie. Fuzzy řízení a jeho kombinace s neuronovými sítěmi bylo velmi široce aplikováno nejprve v Japonsku, a pak téměř všude. To ještě neříká nic o tom, jak dlouho SC vydrží jako živá a podnětná vědecko-výzkumná disciplína. Vzpomeňme na kybernetiku, ještě nedávno renomovanou (a před lety v komunistickém bloku „ideologicky zatracovanou“). Zajisté přinesla velmi významné podněty trvalé hodnoty, ale jaksi trochu „vyšla z módy“. Umělá inteligence (ostatně v mnohém našemu SC velmi blízká) stále patří k důležitým oborům informatiky, původní očekávání se však nesplnila. Expertní systémy zaznamenaly náhlý rozmach, ale dnes se už o nich moc nemluví. Každý takový nový směr má, zdá se, první údobí přehnaných očekávání, pak možná údobí skepse, a nakonec se nějak stabilizuje. I když se třeba o něm úplně přestane mluvit, je důležité, zda něco nového přinesl, něco, co se stalo samozřejmou součástí něčeho jiného. (U expertních systémů to třeba je pojem explicitní reprezentace a zpracování znalostí na počítači.) Dnes ještě patrně nelze odhadnout, jak to se soft computing dopadne. Pokládám však za evidentní, že SC přináší řadu podnětů k spojování (kreativní fúzi, jak někteří říkají) různých přístupů k netradičnímu řešení řady problémů, přístupů dosud rozvíjených izolovaně; a také řadu podnětů k vědeckému bádání na solidních základech těchto přístupů. Je tak výzvou, kterou není dobré přeslechnout; je třeba ji kriticky zhodnotit. Dovolím si skončit heslem, které na jednom z Fór 2000 v souvislosti s informatickou společností vyslovil Martin Bangemann, tehdy komisař EU: Od dat k informacím, od informací k znalostem, od znalostí k moudrosti.
Expertní systémy zaznamenaly náhlý rozmach, ale dnes se už o nich moc nemluví. Každý takový nový směr má, zdá se, první údobí přehnaných očekávání, pak možná údobí skepse, a nakonec se nějak stabilizuje. I když se třeba o něm úplně přestane mluvit, je důležité, zda něco nového přinesl, něco, co se stalo samozřejmou součástí něčeho jiného. (U expertních systémů to třeba je pojem explicitní reprezentace a zpracování znalostí na počítači.) Dnes ještě patrně nelze odhadnout, jak to se soft computing dopadne. Pokládám však za evidentní, že SC přináší řadu podnětů k spojování (kreativní fúzi, jak někteří říkají) různých přístupů k netradičnímu řešení řady problémů, přístupů dosud rozvíjených izolovaně; a také řadu podnětů k vědeckému bádání na solidních základech těchto přístupů. Je tak výzvou, kterou není dobré přeslechnout; je třeba ji kriticky zhodnotit. Dovolím si skončit heslem, které na jednom z Fór 2000 v souvislosti s informatickou společností vyslovil Martin Bangemann, tehdy komisař EU: Od dat k informacím, od informací k znalostem, od znalostí k moudrosti.
Literatura
[1] M. Novák, O. Kufudaki, P. Moos, P. Musílek, E. Pelikán: Umělé neuronové sítě – teorie a aplikace, C. H. Beck, Praha 1998[2] V. Novák: Fuzzy množiny a jejich aplikace, SNTL, Praha 1986
[3] J. Šíma, P. Neruda: Teoretické otázky neuronových sítí, Matfyzpress, Praha 1996
[4] P. Hájek: Metamathematics of fuzzy logic, Kluwer 1998
[5] P. Hájek, T. Havránek, R. Jiroušek: Uncertain Information Processing in Expert Systems, CRC Press 1992
Poznámky
Ke stažení
 Článek ve formátu PDF [259,89 kB]
Článek ve formátu PDF [259,89 kB]