Prokrustes, deformace a nová morfometrie
V současné době jsme svědky „tiché exploze“ v disciplíně, která se minimálně poslední půlstoletí zdála být stranou všech výstřelků a převratných změn. Touto disciplínou je biometrie a kamenem, který rozčeřil její stojaté vody, je soubor statistických technik, označovaný souhrnným termínem „nová morfometrie“, nebo přesněji „geometrická morfometrie“.
Biometrie je když...
Biometrii si můžeme stručně definovat jako aplikaci statistických metod na biologické problémy. Po většinu 20. století se metody biometrické analýzy dělily do dvou základních skupin, založených na vzájemně zcela odlišných konceptuálních rámcích, přičemž neslučitelnost obou přístupů pramenila z různého pohledu na to, co je vlastně zkoumáno a měřeno.Tradiční biometrie
 Původnější a také mnohem rozšířenější jsou metody „klasické“ vícerozměrné statistiky, navazující na práce zakladatelů moderní biometrie – F. Galtona, K. Pearsona, S. Wrighta a R. A. Fishera. Kořeny tradiční biometrie však sahají mnohem dále do minulosti, dokonce až do dob, kdy moderní věda, jak ji vnímáme dnes, teprve čekala na svůj zrod. S trochou nadsázky se dá říci, že dávno předtím, než mohly vůbec být formulovány myšlenky biometrické statistiky, museli vojevůdci a krejčí rozumět proměnlivosti ve velikosti lidí tisíce let předtím, než se kvantitativní biologie mohla stát něčím víc než jen výstředním koníčkem. Ve své typické podobě jsou tradiční techniky vícerozměrné analýzy dat (regrese, faktorová, shluková a diskriminační analýza, analýza hlavních komponent aj.) založeny na obecných principech maticové algebry a není náhoda, že většina používaných metod má širší využití – např. faktorová analýza funguje stejně dobře v psychiatrii jako v botanice nebo zoologii. Vstupní data se většinou získávají měřením vzdáleností, úhlů, ploch apod. Typickými výstupy jsou pak buď různé tabulky, nebo klasifikační grafy (dendrogramy, souřadnicové dvou- i třírozměrné diagramy ad.). Z toho plyne, že ačkoli tyto techniky vznikly v kontextu striktně morfometrických otázek, jejich výsledky neobsahovaly žádnou geometrickou informaci (nebylo např. možno zpětně rekonstruovat původní tvar objektu) – jinými slovy síla biometrických metod tkvěla paradoxně v odstranění té části informace, která byla nejvíce biometrická.
Původnější a také mnohem rozšířenější jsou metody „klasické“ vícerozměrné statistiky, navazující na práce zakladatelů moderní biometrie – F. Galtona, K. Pearsona, S. Wrighta a R. A. Fishera. Kořeny tradiční biometrie však sahají mnohem dále do minulosti, dokonce až do dob, kdy moderní věda, jak ji vnímáme dnes, teprve čekala na svůj zrod. S trochou nadsázky se dá říci, že dávno předtím, než mohly vůbec být formulovány myšlenky biometrické statistiky, museli vojevůdci a krejčí rozumět proměnlivosti ve velikosti lidí tisíce let předtím, než se kvantitativní biologie mohla stát něčím víc než jen výstředním koníčkem. Ve své typické podobě jsou tradiční techniky vícerozměrné analýzy dat (regrese, faktorová, shluková a diskriminační analýza, analýza hlavních komponent aj.) založeny na obecných principech maticové algebry a není náhoda, že většina používaných metod má širší využití – např. faktorová analýza funguje stejně dobře v psychiatrii jako v botanice nebo zoologii. Vstupní data se většinou získávají měřením vzdáleností, úhlů, ploch apod. Typickými výstupy jsou pak buď různé tabulky, nebo klasifikační grafy (dendrogramy, souřadnicové dvou- i třírozměrné diagramy ad.). Z toho plyne, že ačkoli tyto techniky vznikly v kontextu striktně morfometrických otázek, jejich výsledky neobsahovaly žádnou geometrickou informaci (nebylo např. možno zpětně rekonstruovat původní tvar objektu) – jinými slovy síla biometrických metod tkvěla paradoxně v odstranění té části informace, která byla nejvíce biometrická.
Transformace koordinát
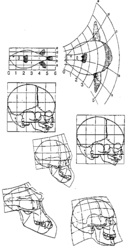
 Zcela odlišnou strategií je přímá vizualizace změn tvaru biologických objektů formou deformace sítě pravoúhlých (karteziánských) souřadnic. Přestože tato metoda bývá nejčastěji spojována se jménem britského přírodovědce sira D’Arcy W. Thompsona a jeho knihou O růstu a formě z r. 1917, její tradice je o několik století starší a sahá až do období renezance. První „transformační sítě“ (viz např. Albrecht Dürer, Vier Bücher von Menschlicher Proportion) odrážely úsilí renezančních umělců obsáhnout v realistickém ztvárnění proměnlivost lidských typů. Toto zaujetí pro postižení obecných zákonitostí okolního světa vedlo renezančního (stejně jako před ním antického) umělce k snahám definovat abstraktně dokonalé proporce zakódované do soustavy matematicky vyjádřených kánonů, a tento „diktát dokonalosti“ byl překonán až nástupem barokní, mysticky exaltované rozmáchlosti.
Zcela odlišnou strategií je přímá vizualizace změn tvaru biologických objektů formou deformace sítě pravoúhlých (karteziánských) souřadnic. Přestože tato metoda bývá nejčastěji spojována se jménem britského přírodovědce sira D’Arcy W. Thompsona a jeho knihou O růstu a formě z r. 1917, její tradice je o několik století starší a sahá až do období renezance. První „transformační sítě“ (viz např. Albrecht Dürer, Vier Bücher von Menschlicher Proportion) odrážely úsilí renezančních umělců obsáhnout v realistickém ztvárnění proměnlivost lidských typů. Toto zaujetí pro postižení obecných zákonitostí okolního světa vedlo renezančního (stejně jako před ním antického) umělce k snahám definovat abstraktně dokonalé proporce zakódované do soustavy matematicky vyjádřených kánonů, a tento „diktát dokonalosti“ byl překonán až nástupem barokní, mysticky exaltované rozmáchlosti.
Nicméně základní konceptuální východiska transformace tvaru jako objektu biometrického zkoumání poprvé explicitně formuloval právě D’Arcy Thompson. Jeho filozofie vycházela z platonského přesvědčení, že proměnlivost forem v přírodě je určitým způsobem uspořádána a ovlivňována více či méně jednoduchou a poznatelnou soustavou usměrňujících sil a že složité tvary organizmů lze převést na jednoduchý systém pravoúhlých souřadnic. Tvar těla příbuzných druhů je tak možno vzájemně odvodit ze změn (deformací) karteziánské sítě, proložené libovolně zvolenými body či částmi objektu (obrázek).
Transformační analýza, v zásadě omezená pouze na grafické výstupy, však postrádá jakoukoli kvantifikaci. Navíc Thompson a jeho následovníci kreslili sítě subjektivně, takže myšlené body sloužící jako vodítko při deformaci sítě většinou postrádaly biologické opodstatnění. A právě tyto skutečnosti byly až donedávna stínem, který – přes snahy několika generací matematicky orientovaných biologů přitahovaných jejím elegantním grafickým stylem – tato metoda nedokázala překročit.
„Moderní syntéza“
Na počátku nové kapitoly v historii biometrie byla snaha nalézt takovou metodu vícerozměrné statistické analýzy, která by umožnila studovat změny v poloze určitých bodů na objektu (význačných bodů, landmarks), a to přímo, nikoli ve formě délek, koeficientů či hlavních komponent. Tyto body jsou (nebo by alespoň měly být) mezi studovanými objekty homologické, takže můžeme zkoumat a vysvětlovat morfogenetické procesy, které je formují, a jejich srovnávání je tudíž z ontogenetického i evolučního hlediska smysluplné. Přímé zkoumání je umožněno jejich přesnou lokalizací ve dvou- či třírozměrném prostoru pomocí souřadnicové sítě. Dvojice (trojice) souřadnic potom slouží k definování několika algebraických veličin, které (a to je významné) umožňují nejen jejich další zpracování konvenčními statistickými postupy, ale zároveň i přímou vizualizaci graficky přehlednou formou. Jinými slovy jde o syntézu obou výše zmíněných základních filozofií.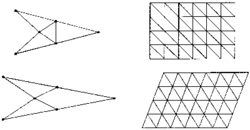
Prokrustes & spol.
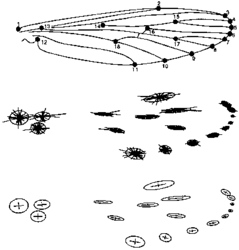
Než si přiblížíme některé z technik nové morfometrie, je třeba se stručně zmínit o Prokrustově analýze, která je rovněž založena na zkoumání tvaru pomocí význačných bodů. Kořeny této metody sahají do přelomu 60. a 70. let, využívat se však začala až v posledním desetiletí. Nazvána byla po bájném obrovi řecké mytologie, který přepadal pocestné, přičemž kratší natahoval na délku svého lože a delší naopak useknutím nohou zkracoval. Toto přiléhavé pojmenování vyjadřuje samu podstatu superpoziční techniky, jejímž cílem je s využitím rotace, posunu a celkové změny velikosti dosáhnout takové konfigurace význačných bodů dvou a více objektů, aby byla optimalizována určitá míra shody, v tomto případě suma druhých mocnin vzdáleností mezi příslušnými homologickými body těchto objektů (podobně jako např. u obyčejné lineární regrese). Proto se této technice někdy říká Least Squares, zkráceně LS, při více než dvou objektech potom Generalized Least Squares, GLS; viz slovníček (rámeček 1).Výsledky superpozičních analýz jsou prezentovány obvykle graficky, např. formou vektorů znázorňujících směr a velikost odchylek jednotlivých bodů od referenční (tangenciální) konfigurace. Tou může být např. předem určený jednotlivý objekt nebo průměrná konfigurace všech srovnávaných objektů (obrázek). Tvarové vzdálenosti mezi objekty je možno kvantifikovat a dále zpracovat některou z obvyklých morfometrických technik (shlukovou analýzou apod.).
Avšak i tato metoda má některá omezení a nedostatky, z nichž nejzávažnější se týkají nemožnosti detekce složitějších tvarových odlišností a lokálních deformací a s tím spojené ztráty podstatné části informace. Nicméně díky své jednoduchosti je Prokrustova analýza i její varianty (např. GRF, viz obrázek) obzvláště výhodná jako prostředek předběžné analýzy dat a při testování jednodušších nulových hypotéz. Prokrustovská procedura je navíc nedílnou součástí složitějších metod geometrické morfometrie.
Co je geometrická morfometrie?
Na rozdíl od superpozičních technik jsou metody geometrické morfometrie ve své podstatě deformační. Výhodou těchto metod je možnost rozlišit uniformní (afinní) deformace (obrázek) od neafinních, nepravidelných změn tvaru. Historicky nejpůvodnější je metoda ohebných pásků (Thin Plate Spline, TPS), kterou její tvůrce, Fred Bookstein z Michiganské univerzity, poprvé představil r. 1989. Základní myšlenkou je – podobně jako u transformovaných koordinát – umístit síť souřadnic na zobrazený referenční objekt, a potom ji tvarovat spolu s obrázkem, dokud není dosaženo shody s objektem srovnávaným. Rozdíly mezi nimi jsou pak ukázány ve formě lokálních deformací původně pravoúhlé sítě (obrázek). Oproti Thompsonovu přístupu však metoda ohebných pásků postrádá jakoukoli subjektivitu, neboť poloha každého bodu je v prostoru jednoznačně určena. Síť zde není vlastním objektem analýzy jako u Thompsona, ale naopak prostředkem zobrazení, komunikačním médiem zprostředkujícím výsledky biologické analýzy.Analýza relativních deformací (Thin Plate Spline Relative Warps, TPSRW), odvozená z metody ohebných pásků, umožňuje srovnání více než dvou objektů najednou. V podstatě je obdobou analýzy hlavních komponent (PCA): relativní deformace představují eigenvektory vypočtené z matice deformační energie. Přitom platí, že čím má deformace menší rozsah (čím je lokálnější), tím je tato energie vyšší. Výsledkem jsou pozitivní a negativní deformace sítě, které ukazují, jak by daný objekt vypadal, kdyby jeho hodnoty relativních deformací (RW-skóre) byly umístěny na opačných koncích jedné z os relativních deformací a zároveň v nulové pozici na osách ostatních (obrázek a). Stejně jako u běžné PCA je možno pro každou z relativních deformací vypočítat např. procento celkové variance vyjádřené jednotlivými komponentami a skóre relativních deformací pro každý objekt (obrázek b a c). Podobně jako u Prokrustovy analýzy je klíčovým krokem stanovení referenčního objektu. Tím může být mladší ontogenetické stadium, předpokládaný evoluční předek nebo průměrná konfigurace, stanovená právě prokrustovskou metodou. 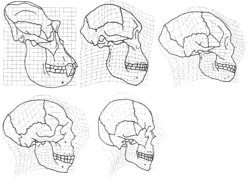
Geometrická morfometrie dnes
Geometrická morfometrie bezesporu znamená kvalitativně zcela nový přístup ke studiu tvaru organizmů. Spojuje v sobě přímé zkoumání homologických význačných bodů, které umožňují zpětnou rekonstrukci tvaru studovaných objektů, separaci lineárních tvarových změn od lokálních nelineárních deformací vizualizovaných formou deformačních sítí a jejich matematické zpracování účinným statistickým aparátem. Díky těmto metodám lze studovat nejen morfologické rozdíly mezi organizmy, ale také hodnotit a vysvětlovat biologické procesy, které tyto změny způsobily (selektivní tlaky apod.).V posledních letech si tento nový směr získává stále více přívrženců. Kromě možností využití v zoologii a botanice (systematické a evoluční vztahy mezi organizmy, studium asymetrie, pohlavní dimorfizmus apod.) nachází geometrická morfometrie uplatnění i v takových oborech, jako jsou paleontologie, paleoarcheologie (tvar ručních sekyr) a medicína. Příkladem jejího využití v lékařství je např. sledování změn tvaru srdečních komor v průběhu některých koronárních onemocnění nebo rozdílů v zakřivení corpus callosum u pacientů trpících schizofrenií. (Pro zajímavost: byly sledovány sagitální „řezy“ 13 schizofreniků z psychiatrické jednotky fakultní nemocnice při Michiganské univerzitě – jako srovnávací vzorek „normálních“ jedinců pak posloužilo 12 lékařů a studentů z téže nemocnice.) Zdá se, že vývoj na poli geometrické morfometrie nabírá na obrátkách. Narůstá snaha zkoumat tvar v trojrozměrném prostoru nebo pokusy překonat nevýhody plynoucí z faktu, že na mnoha biologických objektech lze nalézt jen velice omezený počet význačných bodů. Významnými pomocníky při tvarovém zachycení struktur se stávají magnetická rezonance, počítačová tomografie či laserové digitizéry. Zatím lze jen konstatovat, že nově narozené dítě se má čile k světu a teprve budoucnost ukáže jeho životaschopnost.
Literatura
Bookstein F. L.: Morphometric tools for landmark data. Cambridge University Press, Cambridge 1991Bookstein F. L.: s. 12–40, in L. F. Marcus, E. Bello, A. García-Valdecasas (eds.), Contribution to morphometrics. Madrid, Monografias del Mus. Nac. de Cienc. Nat. 1993
Loy A., Corti M. & Marcus L. F.: s. 215–240, in L. F. Marcus, E. Bello & A. García-Valdecasas (eds.), Contribution to morphometrics. Madrid: Monografias del Mus. Nac. de Cienc. Nat. 1993
Marcus L. F., Corti M., Loy A., Naylor G. J. P., Slice D. E. (eds.): Advances in morphometrics. NATO ASI Series A: Life Sciences, Vol. 284. Plenum Press, New York 1996
Rohlf F. J. & Bookstein F. L. (eds.): Proceedings of the Michigan morphometric workshop. University of Michigan Museums, Ann. Arbor. 1990
Rohlf F. J., Slice D.: Syst. Zool. 39, 40–59, 1990
SLOVNÍČEK
afinní změna tvaru – natažení, nebo naopak stlačení celého objektu podél jedné z ortogonálních (pravoúhlých) os, při němž zůstává zachována rovnoběžnost přímek
analýza hlavních komponent (Principal Components Analysis, PCA) – konstrukce lineárních kombinací původních proměnných tak, aby odčerpávaly co nejvíce jejich celkové variability, kterou je tak možno charakterizovat pomocí redukovaného počtu proměnných, jednotlivé osy jsou navzájem kolmé
deformační energie (energie ohybu, bending energy) – metafora vypůjčená z mechaniky tenkých kovových desek. Představa je založena na konfiguraci bodů umístěných na nekonečně velké, nekonečně tenké ploché kovové desce, kterou je nutno různým ohýbáním deformovat tak, aby bylo dosaženo žádoucího posunu jednotlivých bodů; deformační energie potom představuje idealizovanou energii, kterou je nutno vynaložit k těmto „tvarovým změnám“ – její velikost je tudíž inverzně úměrná rozsahu ohybu: čím je deformace lokalizovanější, tím je energie vyšší a naopak; extrémním případem je afinní změna tvaru, kdy je deformační energie nulová (deska je nakloněna, nikoli ohnuta)
diskriminační analýza – metoda, která se snaží nalézt funkci umožňující klasifikaci studovaných objektů do skupin; takto získané funkce lze použít pro přiřazování nových objektů k těmto skupinám
edgel (edge element) – extenze pojetí význačného bodu začleněním informace o směru zakřivení objektu v tomto bodě
eigenvector – definuje vztah osy hlavní komponenty (viz PCA) k osám původních dat
eigenvalue – tzv. charakteristické číslo; definuje množství celkové proměnlivosti vyjádřené příslušnou hlavní komponentou (viz PCA)
faktorová analýza – podobně jako PCA patří k metodám redukce počtu proměnných, původně vznikla při vyhodnocování výsledků psychologických testů; v této analýze předpokládáme, že každou vstupující proměnnou můžeme vyjádřit jako lineární funkci nevelkého počtu společných (skrytých) faktorů a jednoho chybového faktoru
GLS (Generalized Least Squares) – Prokrustova analýza pro více než dva objekty (též Generalized Procrustes Analysis)
Prokrustova analýza – metoda umožňující superpozici dvou a více objektů jejich vzájemným posunutím, rotací a uniformní změnou velikosti tak, že je minimalizována suma čtverců vzdáleností jednotlivých význačných bodů od příslušných bodů referenčního (tangenciálního) objektu
tangenciální konfigurace – také referenční konfigurace; souřadnice význačných bodů určitého objektu, který může být buď předem určen, nebo je definován průměry souřadnic všech zkoumaných objektů
tangenciální prostor – aproximace tvarového prostoru tak, aby bylo možno použít konvenční matematický aparát; lze si ho přiblížit jako plochu dotýkající se povrchu koule, který představuje tvarový prostor; místem dotyku je tangenciální konfigurace
TPS (Thin Plate Spline) – metoda ohebných pásků; metoda projekce objektu, určeného souřadnicemi ve dvou- či třírozměrném prostoru, vůči druhému (referenčnímu) objektu pomocí deformace pravoúhlé sítě, definované význačnými body tohoto objektu
TPSRW (Thin Plate Spline Relative Warps) – metoda relativních deformací umožňující srovnání více než dvou objektů najednou; zjednodušeně řečeno, jde o obdobu analýzy hlavních komponent, avšak základem je matice tzv. deformační energie (bending energy)
tvarový prostor – prostor určený souřadnicemi objektů, které byly upraveny Prokrustovou procedurou; protože je zakřivený (lze si ho představit jako povrch koule), je nutno ho transponovat do tangenciálního prostoru, který je plochý
uniformní tvarová změna – viz heslo afinní změna tvaru
význačné body – jsou definovány jako body, na nichž je založeno vysvětlování biologických procesů; za význačný můžeme považovat v podstatě jakýkoli bod na studovaném objektu, který lze opakovaně lokalizovat a který splňuje podmínku homologie mezi objekty, např. místo styku tří lebečních švů, vrcholek výběžku, špička zubu
Sir Ronald Aylmer Fisher (1890–1962)
byl jedním z osmi dětí aukčního licitátora (a jedním z dvojčat, ale jeho bratr zemřel). Získal stipendium na Univerzitě v Cambridži, r. 1912 absolvoval v oboru optika, poté se věnoval matematické fyzice. Mimořádný zájem věnoval rovněž genetice a statistické teorii.
Jako učitel přírodopisu vystřídal několik škol, až si ho všiml Karl Pearson, jeden ze zakladatelů moderní biometrie, a nabídl mu místo přednášejícího na Londýnské univerzitě. Fisher jeho nabídku odmítl a vybral si práci v Rothamstedském výzkumném ústavu zemědělském, čímž se zbavil vzdělávací činnosti, ke které se zjevně nehodil. Fisherova schopnost zvládnout v krátkém čase i nejzapeklitější problémy se brzy stala legendární.
Brzy po roce 1920 vzniklo mezi Fisherem a Pearsonem, oběma bouřlivými a panovačnými, nepřátelství. Mělo to však i pozitivní aspekty, protože Fisher, veden vlastní pomstychtivostí, uvedl na pravou míru řadu Pearsonových chybných výsledků.
V roce 1933, když Pearson z Londýnské univerzity odešel, byla jeho původní katedra rozdělena na katedru statistiky, kterou převzal Pearsonův syn, a nově vzniklou katedru eugeniky, jejímž šéfem se stal Fisher. V roce 1943 pak přijal nabídku na místo vedoucího katedry genetiky v Cambridži a pole statistické teorie opustil. Po odchodu do důchodu působil ještě v Commonwealthské vědecké a průmyslové výzkumné organizaci v australském Adelaide, kde v roce 1962 zemřel na embolii. Rodině, která mu pronajímala pokoj, se zakladatel moderní statistiky a populační genetiky jevil jako záhadný, podivný a často bezdůvodně hrubý člověk.
Sir D’Arcy Wentworth Thompson (1860–1948)
pocházel ze skotského Edinburku. Studoval medicínu ve svém rodišti, přírodní vědy v Cambridži, a postgraduálně studoval na Univerzitě v Dundee, později začleněné do Univerzity sv. Ondřeje. Jako čtyřiadvacetiletý dosáhl místa profesora biologie, ze kterého se po reorganizaci stal post vedoucího katedry přírodních věd Svatoondřejské univerzity. Toto místo zastával až do smrti – plných 64 let!
První Thompsonovy práce byly taxonomické, a především bibliografické. Připravil katalogy prvoků, hub, žahavců a červů a celý život psal slovníky týkající se řeckých ptáků a ryb. Po 41 let působil jako vědecký konzultant Skotské rybářské rady. Když (krátce před smrtí) přednášel v Indii o anatomické stavbě ptáků, držel prý pod paží živou slepici.
Thompson byl obrovitý muž s nepěstěným a rozježeným zrzavým plnovousem. Jeho popularita a prestiž, zvláště v pozdějším věku, byly enormní. První vydání jeho monografie O růstu a formě (1915) procházela stálými úpravami a sám autor ji nikdy nepovažoval za dokončenou. Za cíl považoval redukci biologie na fyziku a matematiku. Jeho myšlenka transformace koordinát má kořeny především v tom, že byl fascinován dílem Albrechta Dürera.
Ke stažení
 Článek ve formátu PDF [420,49 kB]
Článek ve formátu PDF [420,49 kB]















