Alberte, nezlob se

V roce 2022 obdrželi John F. Clauser, Alain Aspect a Anton Zeilinger Nobelovu cenu za fyziku za experimenty prověřující základy kvantové teorie, od níž dnes očekáváme bezmála novou průmyslovou revoluci. Má-li se však kvantová teorie stát více než jen tématem akademických diskusí, musí se něco z jejího myšlenkového aparátu stát běžnou součástí komunikace mezi mnohem širší veřejností, než je tomu dnes. V tomto článku a ve společenské hře se pokusíme podrobně vysvětlit jeden ze stěžejních experimentů, za něž byla loňská Nobelova cena udělena. Klíčovým kandidátem na proniknutí do obecnějšího povědomí je pak pojem kvantového stavu. Nahlédnutí, že se kvantový stav chová do jisté míry jako vektor známý ze středoškolské matematiky, může poskytnout alternativní pohled na realitu a vést k hlubšímu pochopení zvláštního chování obyvatel mikrosvěta.

Stáhněte si společenskou hru Alberte, nezlob se!

Na počátku 20. století fyzici odvážně opustili jistotu klasických objektů. Dovolili elementárním částicím vykazovat vlnové vlastnosti a vlnám přiřkli schopnost chovat se jako částice. Světlo tak dostalo svou nejmenší nedělitelnou částici, která však nepřestala umět interferovat jako vlny na vodě. Někdy od roku 1927 měli fyzici k dispozici správnou (nerelativistickou) teorii mikrosvěta a mohli začít přemýšlet, co to všechno znamená. Pro příběh loňské Nobelovy ceny má stěžejní význam práce Alberta Einsteina. Ten v roce 1935 identifikoval v kvantové teorii, v podobě, jak ji interpretoval dánský fyzik Niels Bohr a jeho následovníci, možnost okamžitého působení na dálku.¹⁾ Takové působení sám Einstein o nějakých dvacet let dříve svou obecnou teorií relativity z fyziky vykázal.

A. Grafické znázornění stavu světla s jedním fotonem šířícím se podél osy z a s rovinou polarizace skloněnou pod úhlem φ = 45° vzhledem k ose x . Fyzici nemohou ztrácet čas kreslením budíků, a tak jejich zkratka pro stavový vektor bude např. |1, z, 45°⟩. B. Stav světla se dvěma fotony, každý s jinou polarizací a opačnými směry šíření.

Kvantový stav a jeho měření

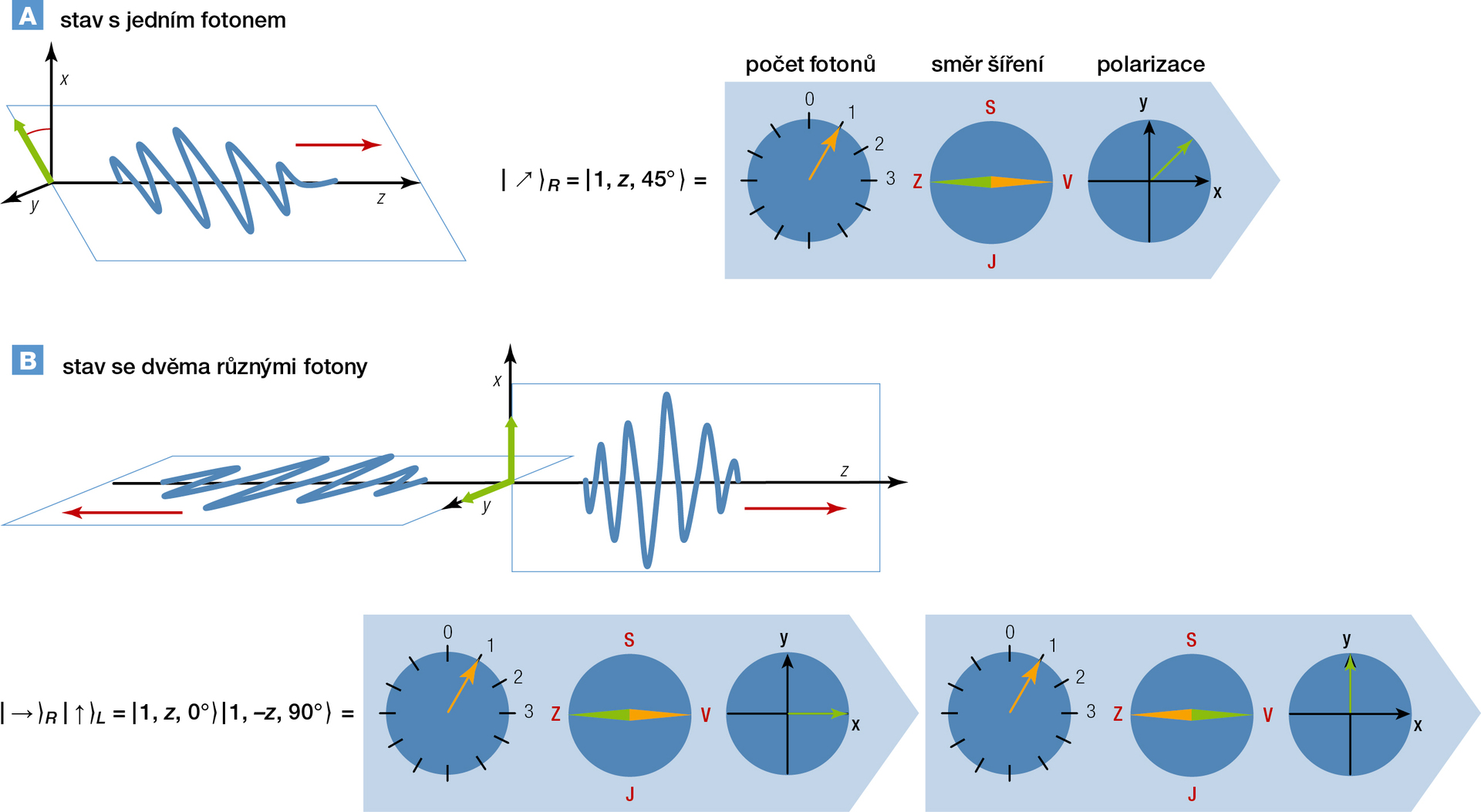
Abychom viděli, v čem spočívá konflikt kvantové teorie s Einsteinovou představou slušné fyzikální teorie, musíme alespoň na chvíli přijmout pojmový aparát kvantové fyziky. Ta popisuje fyzikální systémy pomocí takzvaného stavového vektoru. Jednoduchý stavový vektor si můžeme představovat jako jakýsi ukazatel, „budík“ podobný těm v kabině letadla, který sděluje, v jakém stavu se příslušný systém nachází. Pokud má systém více nezávislých vlastností, stačí vedle sebe „nalepit“ více ukazatelů. Např. světlo může letět v nějakém směru, ale také může být nějakým způsobem polarizováno. Stavový vektor pro paprsek obsahující jednu částici, foton, by mohl vypadat jako na obr. 1a. Lepení „budíků“ vedle sebe lze využít i k popisu stavů s více fotony, např. dvěma – přidáme prostě další budíky odpovídající stavu druhého fotonu. Na obr. 1b máme stav dvou nezávislých fotonů s různými vlastnostmi.

A. Průmět jednotkového vektoru v rovině do dvou zvolených, navzájem kolmých směrů – souřadnicových os – plně určuje směr vektoru. V rovině však existují dva vektory, které sdílejí stejnou složku ve směru osy x . B. Jednotkový vektor lze psát jako součet jednotkových vektorů ve směrech x a y , s příslušnými váhovými faktory. C. Přístroj pro měření polarizace: polarizátor dovoluje průchod pouze světlu, jehož elektrické pole kmitá v nějakém předem daném směru. Zde propouští pouze složku elektrického pole světla ve směru osy x .

Ve skutečném světě se bohužel nemůžeme snadno podívat, v jakém stavu se mikroskopický systém, např. nějaká částice, nachází. Zjištění stavu, tedy odečtení hodnoty na „budíku“, se musí provádět přístrojem – jedná se o měření. Na měření se nejvíce projevuje vektorové chování stavu a také rozdíl mezi chováním mikro- a makroskopických objektů. Kvantový stav je vždy reprezentován vektorem, který má délku jedna, a jeho jedinou podstatnou vlastností je tedy směr.²⁾ Měření stavu v mikrosvětě, které provádějí makroskopičtí pozorovatelé, jako jsme my, vykazuje ovšem jednu zarážející vlastnost. Nedokáže totiž úplně určit směr stavového vektoru. Setkáváme se tu s jakousi slovní hříčkou. Měření dokáže určit stav systému pro budoucnost – systém je ihned po měření přesně ve stavu, ve kterém jsme ho změřili – ale nedokáže určit, jaký byl stav v minulosti. Obvykle máme za to, že nemusíme minulý a budoucí význam slova určit nijak rozlišovat. Ne tak v mikrosvětě. Budoucnost tu není plně determinována stavem v minulosti, je jen jaksi omezena, a zároveň po každém měření zůstává nejistota o tom, jak stav původně vypadal.

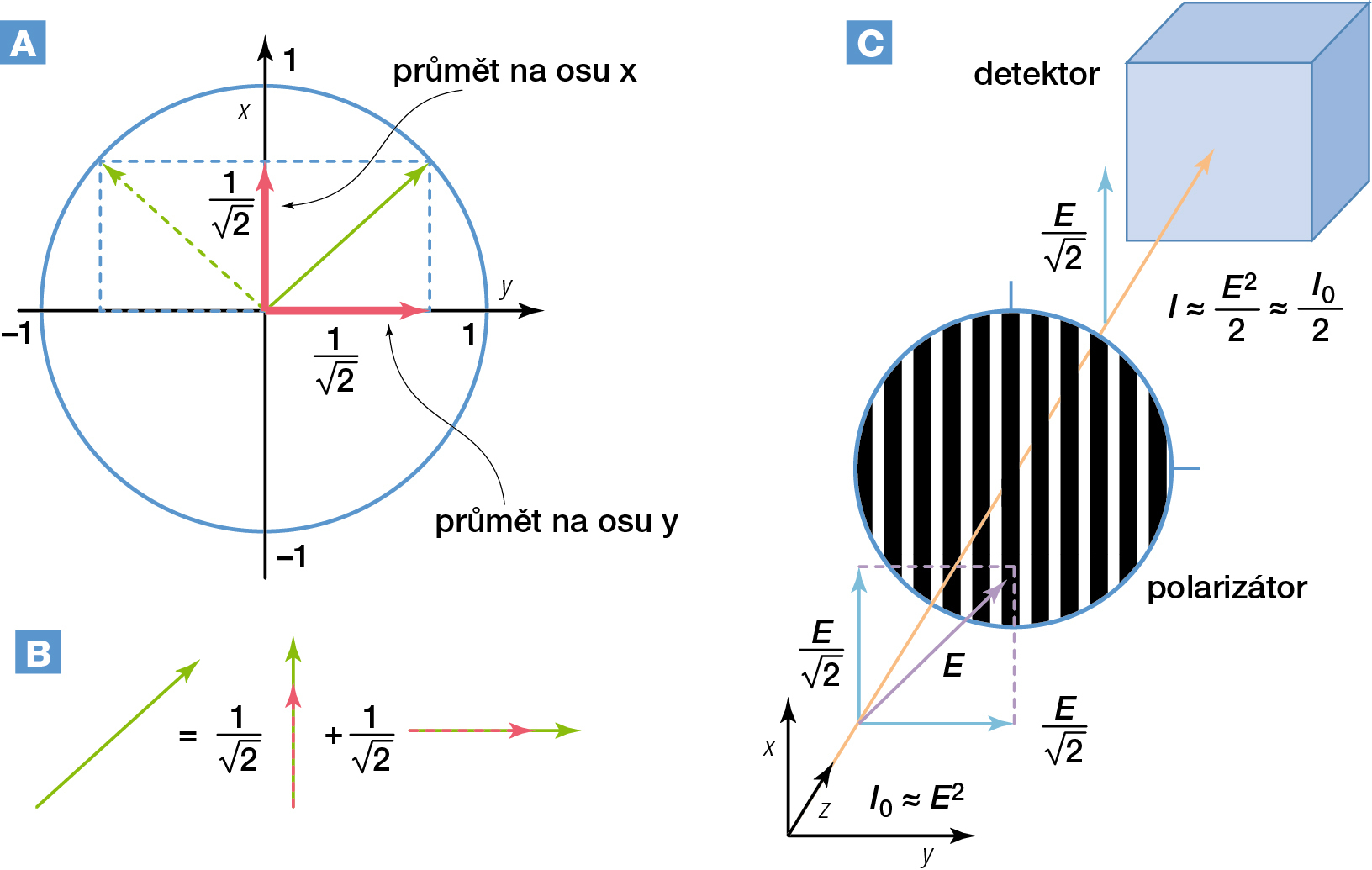
Můžeme si to vysvětlit na měření polarizace světla. Přístroj na její měření by se mohl skládat z detektoru intenzity světla a z polarizátoru, který stojí před detektorem (viz obr. 2). Každé kvantové měření lze chápat tak, že se nejprve vyfiltruje zvolená složka stavu (třeba složka polarizace ve směru osy x) a potom se registruje detektorem, zda systém filtrem prošel, či ne. Představme si paprsek světla polarizovaný pod úhlem 45° vzhledem k ose x. Pokusem zjistíme, že polarizátorem natočeným ve směru x projde přesně polovina energie paprsku. Elektromagnetická teorie světla by tvrdila, že složka vektoru elektrického pole světla ve směru y byla polarizátorem pohlcena a prošla jen složka ve směru x o velikosti E/√2 (obr. 2b). Intenzita světla je dána druhou mocninou elektrického pole, a je tedy podle obr. 2a rovna jedné polovině původní intenzity. Kvantová teorie pracuje s jinou představou: světlo je proud fotonů, jejichž stav popisuje stavový vektor mířící stejným směrem jako polarizace.³⁾ Každý foton projde polarizátorem s pravděpodobností danou tzv. Bornovým pravidlem. To zní: Najdi průmět stavového vektoru do směru charakterizujícího filtr a umocni ho na druhou. To zde vede k pravděpodobnosti průchodu 50 % a k poloviční energii prošlého svazku. Pokud se detekce mnohonásobně opakují, určíme polarizaci světla nastavením úhlu na polarizátoru tak, aby prošla všechna energie. Pokud nás ovšem zajímá stav jednoho konkrétního fotonu, neřekne nám jedno měření polarizace téměř nic. V případě úspěšné detekce netušíme, s jakou pravděpodobností nastala, a původní stav fotonu je nevratně narušen.

Můžeme tedy světlo považovat za proud částic? Chceme-li myslet kvantově, musíme i částicový obraz reality vnímat trochu jinak. Situaci s jedním fotonem letícím směrem k detektoru na obr. 2c bychom správněji měli popisovat slovy: „Světlo se nachází ve stavu s jedním fotonem letícím v kladném směru osy z s polarizací ve směru vzhledem k ose x.“ Tato formulace by nám měla pomoci vidět jako kvantový systém nikoli částice-fotony, ale světlo (elektromagnetické pole), které nabývá různých stavů. Částicový obraz totiž jinak svádí k neadekvátní představě kuliček putujících prostorem. V kvantové teorii tedy nakonec ani pojem částice neznamená to, co v představách klasických.

Kvantový stav a princip superpozice

Každý kvantový stav se chová jako vektor, ať už je systémem elektron, nebo celý vesmír. Obecně postupuje kvantová teorie tak, že každé vlastnosti fyzikálního systému přiřadí sadu navzájem se vylučujících stavů, které ji kompletně popisují. Stav kvantového systému pak známe, když známe projekce skutečného stavu do těchto jeho možných stavů, stejně jako známe vektor na obr. 2a, když známe jeho rozklad do os souřadnicového systému. Kvantový pohled na svět operuje s pojmem stavu – svět, včetně nás samotných, prochází sekvencí stavů,⁴⁾ z nichž my vnímáme (vnímání je jakási obdoba měření) jen nějakou projekci do jisté množiny možných stavů. Možné stavy jsou ty, které naše makroskopické smysly (často „prodloužené“ přístroji) dokážou registrovat. Aby ovšem tento obraz dával úplný smysl, museli bychom ho ještě značně upřesnit a ukázat, že věrně reprodukuje svět, jak ho vnímáme.⁵⁾ Místo toho jenom příměr: konflikt kvantové představy s realitou je obdobný tomu, který svého času řešil Koperníkův heliocentrický model. Ať už se ovšem Země otáčí kolem své osy, nebo ne, i po Koperníkovi vidíme ráno na východě vycházet slunce. Obdobně kvantová teorie odhaluje jistou skrytou „realitu“, jejíž důsledky se shodují s naší každodenní zkušeností, byť může být odvození těchto důsledků značně obtížné. Trvalo tisíce let, než jsme si uvědomili, že stejné fyzikální zákony platí pro pohyb planet i pro naši procházku po Karlově mostě. V kvantové teorii např. platí tzv. princip superpozice: jsou-li nějaké stavy možné, jsou možné i jakékoliv jejich (lineární) kombinace. Ukázat, že to platí i pro stavy nás, inteligentních bytostí, není s plnou přesvědčivostí dnes možné.⁶⁾ Nicméně alespoň dokud se pohybujeme v mikrosvětě, žádnou chybu lpěním na principu superpozice neuděláme.

Pro některé veličiny je superpozice zcela přirozený jev. Polarizace fotonu je kompletně určena dvěma navzájem se vylučujícími stavy – např. stavem polarizovaným ve směru osy x a stavem polarizovaným ve směru osy y (obr. 2a). Průmět vektoru ve směru y do osy x a obráceně je očividně nula, takže systém polarizovaný ve směru osy x není ani trochu ve stavu polarizovaném ve směru osy y – tyto stavy se navzájem vylučují. Jak jsme však viděli, světlo polarizované (vzhledem k ose x) pod nějakým úhlem je polarizované trochu ve směru osy x a trochu ve směru osy y. Vektor, který popisuje tento stav, je součtem stavových vektorů ve směrech x a y se stejnou vahou (obr. 2b). Takový stav označujeme jako superpozici dvou stavů. Ovšem ani pro klasickou teorii nepředstavuje tato superpozice nic neobvyklého.

A. Zjednodušené značení stavů fotonů a provázaný stav dvou fotonů nesoucích různé polarizace a letících různými směry. B. Korelovaná detekce provázaného, nepolarizovaného stavu | Ψ ⟩. Volíme případ, kdy k detekci na detektoru A dochází dříve než na detektoru B. Díky tomu je vybrána (zelené šipky) jen jedna z alternativních složek stavu a do druhého detektoru míří stav s již určenou polarizací.

Kvantové provázání

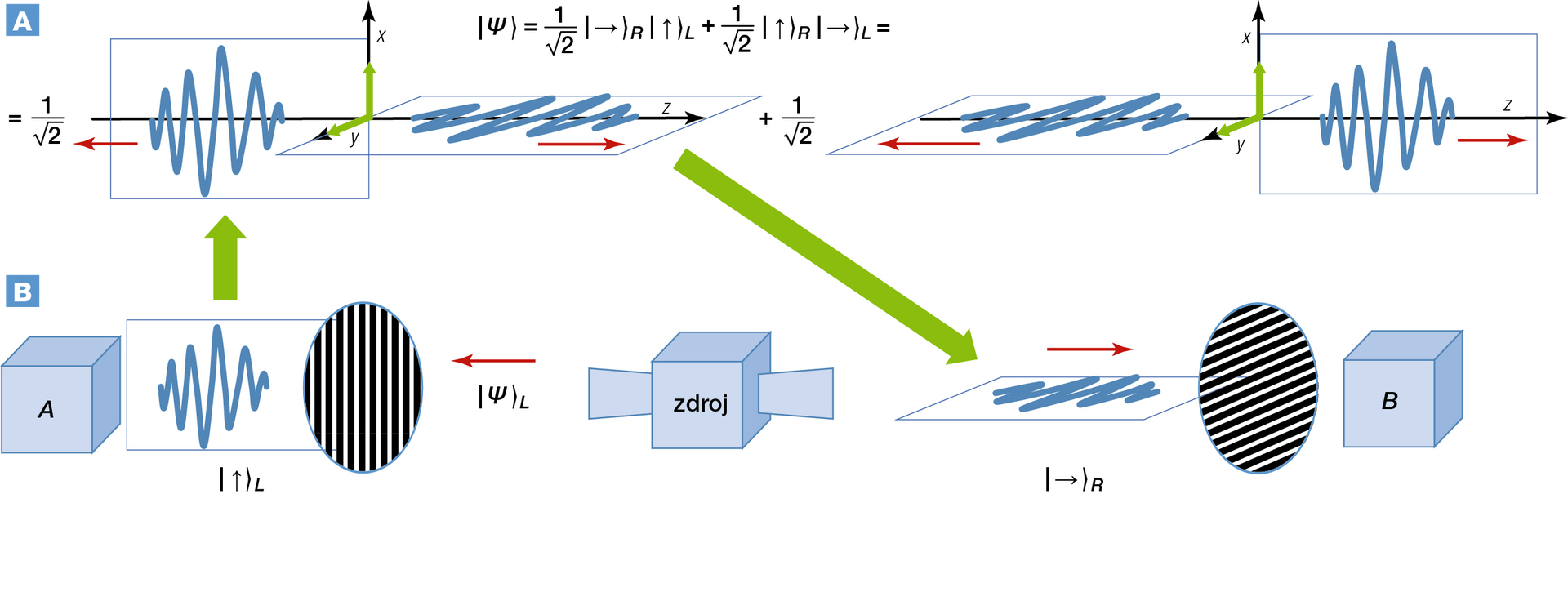
Platí-li princip superpozice obecně, může se světlo se dvěma fotony nacházet i ve stavu podle obr. 3a. Tento stav je superpozicí dvou složek: V jedné letí foton s polarizací ve směru x k detektoru A a foton s polarizací ve směru y k detektoru B. Ve druhé jsou polarizace prohozeny. Tento typ stavu se nazývá kvantově provázaným stavem. Stavy fotonů se tu navzájem podmiňují, jsou provázané, protože měření detektorem A v obr. 3b ovlivňuje měření na detektoru B na druhé straně laboratoře. Jak je to možné? Detektor A určuje stav fotonu, který k němu letí, ale nijak neinteraguje s fotonem, který letí na opačnou stranu laboratoře. Podle Bohrových pravidel kvantové teorie je ovšem případnou registrací fotonu detektorem A nastaveným na směr polarizace x vyloučen jeho stav s polarizací y. Když se podíváme na příslušný stav (obr. 3a), vidíme, že je tím vyloučena i celá příslušná složka, která obsahovala stav s polarizací ve směru x pro foton letící na opačnou stranu. To tedy znamená, že po měření detektorem A už foton letící k detektoru B musí nutně být ve stavu s polarizací ve směru y. Dokonalý detektor B, nastavený na směr y, by nutně zahlásil detekci fotonu. Při opakování experimentu budou oba detektory hlásit foton s pravděpodobností 50 %, ale budou tak činit korelovaně, vždy budou detekovat (nebo naopak nedetekovat) foton společně.

Kvantová nelokalita a Bellova nerovnost

Experimentálnímu důkazu takového chování však stojí v cestě jeden zásadní problém. Korelované detekce mohou pochopitelně nastat i u stavů, které vůbec nejsou provázané a mají každý od začátku polarizaci zajišťující detekci (nebo její absenci) na daném detektoru. Co když s takovými pracujeme? O stavech světla se nemůžeme nějak nezávisle ujistit, že vypadají, jak potřebujeme. V Bohrově popisu experimentu ovlivníme detekcí na jedné straně laboratoře okamžitě stav fotonu na straně druhé. Něco takového pochopitelně nemohl Albert Einstein, autor speciální a obecné teorie relativity, připustit. Dokonce i pokud by to bylo správně, musela by podle Einsteina existovat alternativní teorie, která kvantové chování vysvětluje odkazem na nějakou informaci, obsaženou ve fotonech již od počátku ve formě tzv. skrytých parametrů. Také stav na obr. 3a, který žádné skryté parametry nemá, musí být podle Einsteina reprezentovatelný alternativní teorií se skrytými parametry. Z experimentu s perfektní korelací mezi detektory tedy ještě nemůžeme dospět k závěru, že korelace měření na různých místech prostoru v důsledku provázání – tzv. kvantová nelokalita – je skutečnou vlastností přírody.

Aby mohl být spor Einsteina s Bohrem rozhodnut, musel nejprve v roce 1964 John S. Bell ukázat, že některé předpovědi kvantové teorie nejsou slučitelné s žádnou teorií skrytých parametrů. Formuloval nerovnost, která se prověřuje v experimentu, za nějž byla vloni udělena Nobelova cena. Na základě tohoto experimentu si také můžete zahrát společenskou hru. Experiment je vyobrazen na herním plánu. Na základě detekcí fotonů, které simulujeme vrhy kostkou, počítáme ve hře hodnotu S levé strany slavné Bellovy nerovnosti. Podrobně ji odvozujeme a vysvětlujeme v pravidlech hry. Pro náš případ zní:

S = |⟨a₁b₁⟩ – ⟨a₁b₂⟩| + |⟨a₂b₁⟩ + ⟨a₂b₂⟩| ≤ 2.

Bellova nerovnost říká, že pokud jsou výsledky měření a1, a2, b1 a b2 v příslušném experimentu určeny lokálně, tj. z informace dopravené fotony na místo detekce (což ve hře simulujeme), musí být hodnota S menší nebo rovna 2. Bellova nerovnost je formulována pomocí dnes již rutinně měřitelných středních (průměrných) hodnot veličin odečtených na čtyřech různě nastavitelných detektorech (viz hrací plán). Ukazuje se, že při vhodném nastavení úhlů na polarizátorech detektorů je pro stav z obr. 3a možné naměřit velikost veličiny S až ve výši 2√ 2 ≅ 2,83. To je velikost nedosažitelná žádným neprovázaným stavem. Ve hře simulujeme i tento případ při nastavení detektorů tak, aby se nám snadno počítaly pravděpodobnosti. To vede právě na hraniční hodnotu S = 2. Jak si však lze ve hře ověřit, i hodnota 2 je v experimentu s neprovázanými fotony krajně nepravděpodobná. V diskusi ke hře čtenář snadno nahlédne, jak by musel nastavit polarizátory, aby byla magická hodnota 2 překonána.

Nobelova cena za fyziku 2022

Již v roce 1972 dokázal John F. Clauser realizovat experiment demonstrující porušení Bellovy nerovnosti.⁷⁾ John Bell, který se ve slavném sporu původně přikláněl spíše na stranu Einsteina, však poukázal na jistá zadní vrátka Clauserova experimentu, kterými by se teorie skrytých parametrů mohla vrátit do hry. Proto byl v roce 1982 Alainem Aspectem a jeho skupinou realizován experiment⁸⁾ přibližně v podobě, jak ho popisujeme v naší hře, tj. s náhodným přepínáním použitých detektorů. Další experimenty postupně uzavřely všechna (známá) realistická zadní vrátka, a tak jsou fyzici dnes velkou většinou přesvědčeni o platnosti nelokálních předpovědí kvantové teorie. Takže, Alberte, nezlob se, ale nelokální korelace v přírodě skutečně existují.

Přesto se však Einsteinova obava, že provázanými stavy lze porušit zákaz šíření informace rychleji než světlo, nepotvrdila. Dnes známe důkaz, že provázané stavy nelze využít k okamžitému předávání informace. Ani kvantová teleportace, klíčový jev pro kvantové počítače a pro budoucí kvantové technologie, který demonstroval Anton Zeilinger, nedokáže přenášet informaci rychleji než světlo. V jistém smyslu tu tedy platí okřídlené konstatování o vlku a koze, i když těžko soudit, zda by byl Einstein spokojen.

Námitky různého kalibru proti kvantové teorii stále trvají. Mnohé její interpretační otázky totiž nemají své „Bellovy nerovnosti“, a postrádají tak experimenty, které by je mohly rozhodnout. Nedostatek hlubšího porozumění základům kvantové teorie nemusí v nejbližších desítkách let nutně překážet naší touze stále účinněji ovládat přírodu. Naštěstí i bez této motivace máme neutuchající touhu rozumět. John S. Bell zemřel v roce 1990 ve věku 62 let, a jeho průkopnická práce tak Nobelovou cenou oceněna nebyla. Kvantová teorie však dnes čeká na další podobné průkopníky, kteří by dokázali přetavit existující, často metafyzické námitky proti ní do formy proveditelných experimentů.