Chůze v davu: impulzy bez doteku

„Nejednou nás chybný krok ponořil až ke stehnům do tmavého rosolovitého bahna, které se na metry kolem nás pod našimi kroky vlnilo. Jeho přilnavá síla nás chytala za paty, i když jsme šli po pěšině, a když jsme – uchýlivše se od ní – klesali do bahna, měli jsme dojem, že nás čísi poťouchlá, zlomyslná ruka stahuje do hnusných hlubin. Tak úporná a cílevědomá byla síla bažin.“

Arthur Conan Doyle: Pes baskervillský

Pro člověka zřejmě existuje jen velice málo samozřejmějších činností, než je pohyb mezi ostatními lidmi. Chůze v davu je pro nás zcela rutinní dovednost a málokdo z nás o ní detailněji přemýšlí. Během samotného pohybu ovšem probíhají v mozku člověka poměrně komplikované vyhodnocovací procedury. Jejich podstatu lze připodobnit k procedurám, na jejichž základě se řidič vozidla rozhoduje o své bezprostřední reakci na aktuální stav dopravního toku. Podobně jako řidič také chodec – jako součást pohybující se skupiny osob – odhaduje parametry pohybu ostatních chodců (typicky rychlost a směr) a predikuje nejbližší vývoj systému. Na základě těchto údajů pak optimalizuje vlastní parametry tak, aby s co možná nejmenším úsilím a za co možná nejkratší čas dosáhl svého cíle. Z matematického hlediska se tedy jedná o specifický, a navíc velmi zajímavý případ optimalizační úlohy řešené v reálném čase. Z fyzikálního pohledu pak dav představuje samořízený systém vzájemně interagujících částic (obecně nazývaných agenty) pohybujících se podle specifických pravidel uvnitř jisté omezené plochy.

Dav jako agentní systém

Příbuznost mezi systémy pohybujících se osob a dvourozměrnými fyzikálními systémy částic je očividná. Ale lze vůbec takovou podobnost nějak využít? Lze pomocí ní například simulovat pohyb skupiny osob? A v čem je naopak největší odlišnost obou systémů? Takové a další otázky si klade poměrně mladá vědní disciplína, nazývaná v anglické literatuře Pedestrian Dynamics (Dynamika chodců).¹⁾ Zaobírá se nejen klasickým pohybem chodců, ale i reakcí davu na vzniklou paniku, kdy se pravidla pohybu i jeho další charakteristiky razantně mění.²⁾

Při snaze simulovat pohybující se dav či analyticky předpovídat jeho vývoj (či parametry) narážíme bohužel na největší komplikaci už při samotném sestavování konkrétního dynamického popisu. Pro každou pohybovou rovnici je totiž nezbytné znát silové působení mezi elementy daného systému. Stejně jako je pro řešení gravitačních úloh nutné znát konkrétní závislost gravitační síly na vzdálenosti objektů (což už za nás vyřešil Isaac Newton, 1642–1727) a tak jako je pro elektrostatiku nutné vědět, jak závisí elektrická síla na vzdálenosti nabitých těles (Charles-Augustin de Coulomb, 1736–1806), tak je pro agentní modelování žádoucí znát, na základě jakých pravidel spolu agenty (chodci, řidiči) interagují. Ovšem povaha agentních sil ve srovnání s klasickými fyzikálními silami snad ani nemůže být odlišnější.

Stochastický model chodce

Ačkoli jsou účinky interakcí mezi chodci zřetelné a přímo měřitelné, impulzy, které je vyvolávají, mají socio-psychologickou podstatu. Zjednodušeně vzato se jedná buď o přitažlivé síly, vyvolané kupříkladu snahou postupovat vpřed za nejrychleji se pohybujícím chodcem, anebo o odpudivé síly, vynucené sociálními konvencemi, jakými jsou například udržování jistého minimálního rozestupu mezi blízkými chodci tak, aby nedošlo k narušení tzv. osobní (či dokonce intimní) zóny chodce. Již z tohoto popisu je zcela jasné, že socio-dynamické síly, tj. síly vyvolané nepřímými socio-psychologickými podněty a projevující se změnami v dynamice pohybu, nejsou detekovatelné žádným přímým měřením. To je v porovnání s gravitačními či elektrickými silami zcela zásadní komplikace.

Lze tedy tyto „impulzy bez doteku“ vůbec popsat matematicky?

K řešení tohoto problému může dobře posloužit jednoduchý fyzikální model sestávající z většího počtu částic pohybujících se v omezené dvourozměrné oblasti. Cílem každé částice je dostat se z jednoho jejího konce na druhý za co možná nejkratší čas. Pohyb ale musí probíhat bezkonfliktně, tj. bez narušování osobních zón ostatních částic. To je v modelu zaručeno přítomností odpudivých sil, které mají následující vektorový tvar:

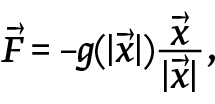
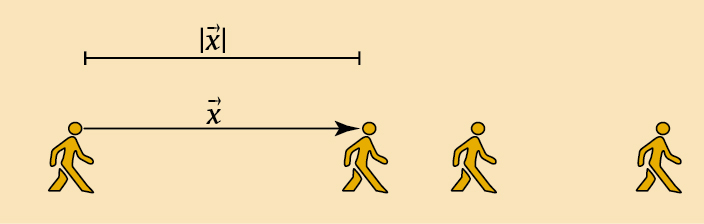
kde x⃗  je vektor propojující danou částici s jejím nejbližším sousedem, |x⃗ | je jeho velikost (obr. 2) a g(|x⃗ |) je repulzivní socio-dynamická síla dosud neznámého tvaru, závislá na vzdálenosti mezi částicemi.

Skupinu pohybujících se lidí lze matematicky popsat podobně jako dvourozměrný fyzikální systém částic. V jednoduchém modelu propojuje danou částici (chodce) s jejím nejbližším sousedem vektor x⃗ o velikosti |x⃗ | (podrobnosti v textu).

Stochastičnost (nahodilé chování) systému, jež zohledňuje skutečnost, že každý chodec reaguje na nastalou situaci individuálně a že dokonce i jeden a tentýž chodec reaguje na totožný podnět v jiném čase odlišně, je do modelu implementována prostřednictvím tzv. faktoru stochastické rezistivity β. Ten buď potlačuje, nebo zesiluje vliv náhody při finální rozhodovací proceduře. Systém s nulovou hodnotou rezistivity je absolutně náhodný, zatímco roste-li rezistivita nade všechny meze, stává se systém zcela deterministickým a nepodléhá žádnému náhodnému šumu.

Model chodce v koridoru

Omezíme-li se na pohyb chodců v úzkém koridoru, který neumožňuje předbíhání, situace se značně zjednoduší, neboť každý chodec je jednoznačně popsán aktuální velikostí rychlosti a aktuální polohou na souřadnicové ose. Příslušná repulzivní síla navíc přechází do skalární podoby:

F(x) = –g(x),

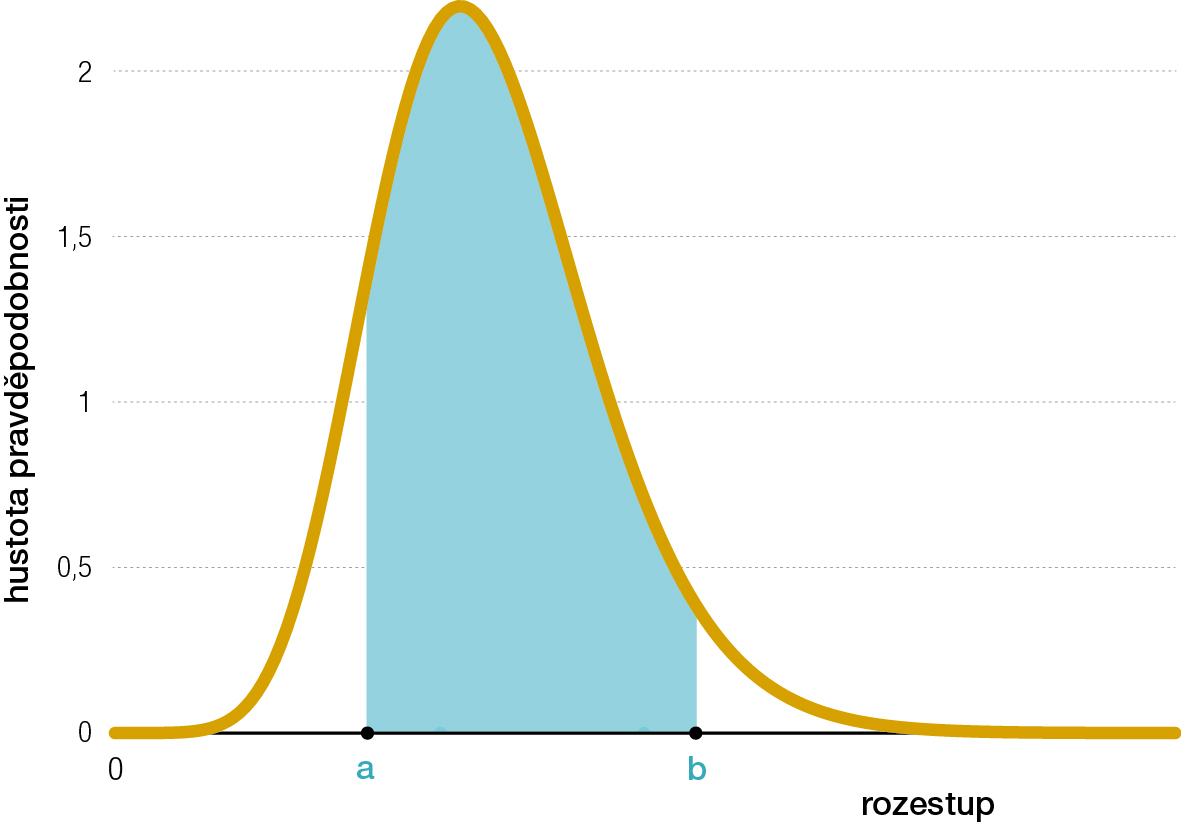
kde x představuje vzdálenost mezi sousedními chodci. Největší výhodou tohoto zúžení je skutečnost, že uvedený model je analyticky řešitelný, tj. k jeho řešení lze dospět čistě matematickými postupy, které nevyužívají žádných zjednodušení ani aproximací. Zvolíme-li pevně funkci g(x) a hodnotu stochastické rezistivity β, vedou příslušné matematické postupy k přesnému tvaru statistického rozdělení rozestupů, tj. k funkci, s jejíž pomocí lze numericky vyčíslit pravděpodobnost, že vzdálenost dvou sousedních chodců (rozestup) leží v intervalu 〈a,b〉. Tuto hodnotu (číslo mezi nulou a jedničkou) získáme totiž integrací (obr. 3). Tím dostaneme kompletní představu o statistickém rozložení chodců v citovaném modelu.

Grafická interpretace výpočtu pravděpodobnosti. Barevná plocha odpovídá pravděpodobnosti, že rozestup sousedních chodců bude číslo náležející intervalu .

Empirické rozdělení rozestupů

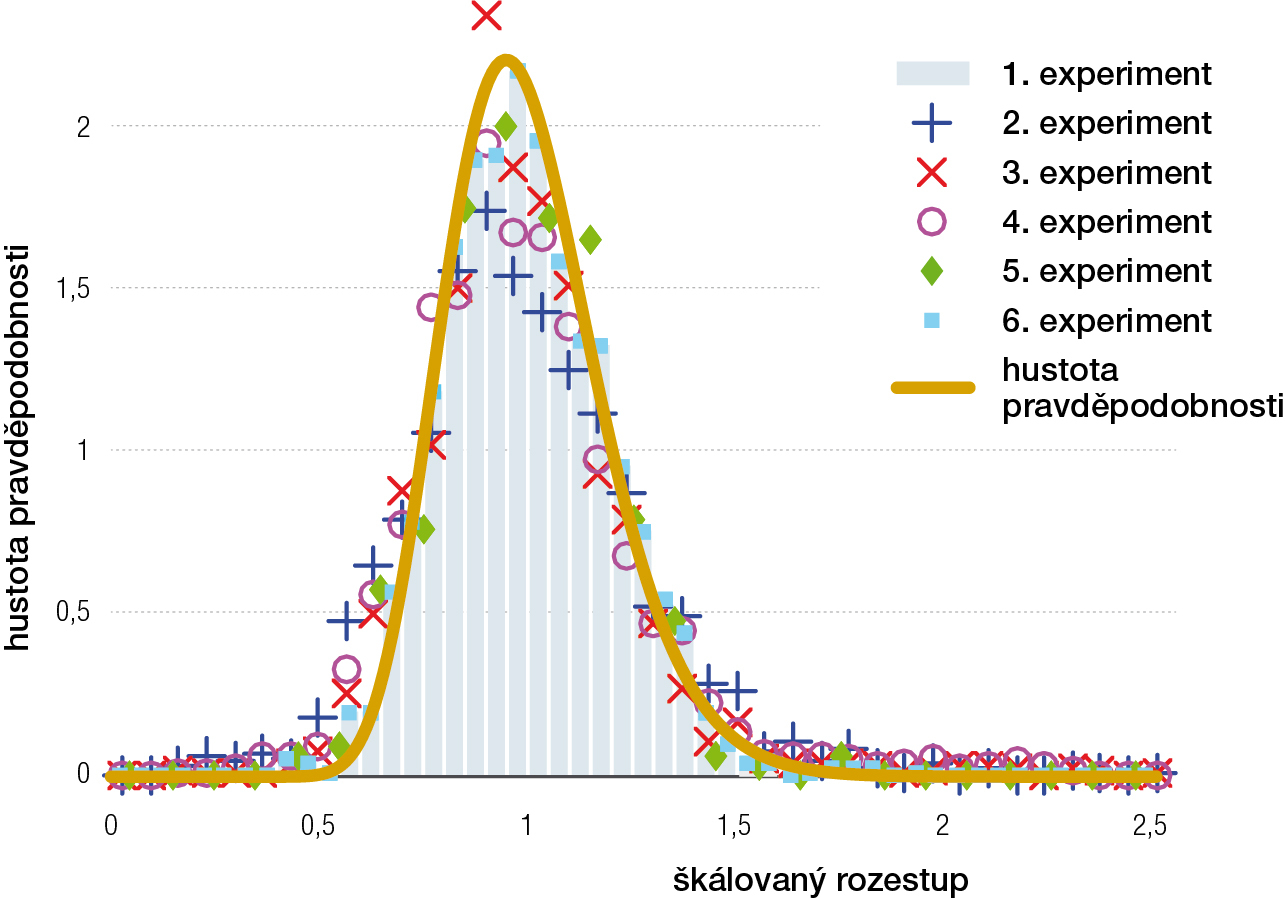
Aby mohl být uvedený koncept využit při detekci skutečných interakčních sil, je nezbytné získat ucelenou představu o tom, jak často se které rozestupy objevují v běžných situacích, tj. při reálném provozu. K tomuto účelu proběhla v posledních letech řada experimentů a měření. Z nich byly získány experimentální, resp. empirické průběhy pravděpodobnostních hustot pro světlosti. K velkému překvapení všech vyšlo najevo, že bez ohledu na typ experimentu nebo způsob či místo měření jsou získané hustoty (obr. 4) vždy ze stejné třídy funkcí, a sice z tzv. GIG distribuční rodiny.³⁾ Jejími charakteristickými znaky jsou enormní pokles pravděpodobnosti pro výskyt velice blízkých chodců a jemný exponenciální pokles pravděpodobnosti pro velké rozestupy.

Statistické rozdělení škálovaných vzdáleností mezi chodci. Výsledky jsou překvapivě podobné bez ohledu na typ experimentu nebo způsob či místo měření.Krbálek M., Hrabák P., Bukáček M.: Pedestrian headways – Reflection of territorial social forces, Physica A 490, 38–49, 2018, DOI: 10.1016/j.physa.2017.08.013

Přitom jedinou odlišností pro různá měření (experimenty) je detekovaná hodnota parametru β, která souvisí zejména se šířkou koridoru a s hustotou proudění, tedy s počtem chodců na jednotce délky. Tímto a sérií dalších analýz⁴⁾ byla prokázána výrazná podobnost socio-dynamických interakcí v různých chodeckých systémech.

Univerzalita socio-dynamických sil

Ještě větším překvapením je ale zjištění, že se rozdělení ze stejné distribuční rodiny objevuje i při analýze statistického uspořádání vozidel v různorodých dopravních systémech (při měření dopravního proudu na všech evropských či amerických dálnicích; při chaotickém průjezdu velkého počtu motorek křižovatkami ve vietnamské Hanoji; při čekání na zelený signál na řízených křižovatkách v Singapuru atd.).⁵⁾ To značí, že socio-dynamické síly mají u chodců i řidičů velice podobný charakter a jejich závislost na vzdálenosti se zjevně řídí stejnou matematickou zákonitostí.

V automobilové dopravě je ale škála hodnot pro parametr β mnohem pestřejší. Zatímco při nízkých hustotách proudění (např. 5 až 10 vozidel na kilometr) je stochastická rezistivita nízká, a systém je proto zatížen výrazným šumem (náhodnými fluktuacemi v chování jednotlivých vozidel), s rostoucí hustotou rezistivita β výrazně stoupá. To koresponduje s obecně známým faktem, že s rostoucí hustotou provozu roste také míra synchronizace pohybu jednotlivých vozidel, která spontánně redukuje stochastickou složku přítomnou v systému. Zajímavostí také je, že mezi hustotami 20 a 35 vozidel na kilometr dochází k dočasnému poklesu rezistivity, a to z důvodu změny dopravní fáze, tj. přechodu z volného proudění na kondenzované. Tato změna se makroskopicky projevuje tím, že zatímco při volné fázi s rostoucí hustotou roste také intenzita (počet vozidel, které minou daný bod za jednotku času), v kondenzované fázi intenzita s rostoucí hustotou naopak klesá. Při mezních hodnotách hustoty může dokonce dopravní proudění, jak dobře známe, zcela ustat.

Univerzalita statistických rozdělení vzdáleností agentů v různých socio-dynamických systémech spočívá ve skutečnosti, že bez ohledu na detailní specifikaci těchto systémů je rozdělení světlostí stále ze stejné distribuční rodiny (GIG). To ukazuje na totožné rozhodovací vzorce, jež jsou pravděpodobně přítomny ve všech takových systémech, kde o dalším pohybu rozhoduje mozek člověka a jeho interakce s ostatními elementy v systému.

Jelikož rozdělení GIG je speciálním případem obecného rozdělení rozestupů, dospíváme k ohromujícímu rozuzlení: Hledaná repulzivní síla působící mezi dvěma blízkými chodci (popř. obecně mezi agenty libovolného socio-dynamického systému) je nepřímo úměrná kvadrátu vzdálenosti obou chodců. Socio-dynamická síla tedy podléhá stejné matematické závislosti na vzdálenosti jako síly gravitační či elektrostatické.

Zdá se tedy, že lidská inteligence při svých rozhodovacích procesech kopíruje přírodní zákony, jimž je člověk sám nucen se podřizovat.

Socio-dynamická síla působící mezi chodci podléhá stejné matematické závislosti na vzdálenosti jako síly gravitační či elektrostatické.Snímek volné dílo, CC0