Barvení grafů včera a dnes

Jako první si tuto otázku v polovině 19. století položil anglický student F. Guthrie. Vyšlo mu, že čtyři barvy stačí na mapu anglických hrabství a na všechny mapy, které zkusil – ale nevěděl, jestli to funguje vždycky. Ukázalo se, že to neví ani žádný ze slovutných profesorů, kterých se zeptal. Po třiceti letech jiný Angličan, A. Kempe, problém vyřešil, za což byl povýšen do rytířského stavu – navzdory tom, že se v jeho řešení později našla chyba a problém zůstal otevřený další dlouhá desetiletí. Až v roce 1976 problém pomocí počítače vyřešili američtí vědci K. Appel a W. Hakken. I v jejich důkazu se posléze objevila nejasná místa a definitivní řešení našla až v roce 1996 skupina matematiků, mezi nimiž byl i český rodák Robin Thomas.

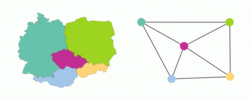Problém, který vznikl jako studentská hříčka, tak zaměstnává přední matematiky už přes 150 let a zájem o něj stále trvá. Všechna známá řešení jsou totiž tak složitá, že pro jejich zvládnutí je potřeba počítač. Během řešení problému (a díky němu) se rozvinula nová matematická disciplína, teorie grafů: Dovnitř každého státu si nakreslíme bod (vrchol). Pokud spolu dva státy sousedí, jejich vrcholy spojíme čarou (hranou). Dostaneme něco, čemu se říká graf, v tomto případě rovinný, tj. nakreslený bez křížení hran na rovinu – list papíru. Na státy můžeme zapomenout, a budeme barvit jenom jejich reprezentace, vrcholy, přičemž stejně barevné vrcholy nesmějí být spojené hranou. Tím se problém nezměnil, ale je lépe vidět, co je důležité, a je možné o řešení lépe přemýšlet. Ale hlavně se tato formulace hodí na problémy úplně jiného typu, někdy i praktické.