Orbis pictus

John Barrow je uznávaný a neobyčejně plodný vědec, pracující především v kosmologii – počet jeho původních časopiseckých publikací jde do stovek. Je také velmi úspěšným autorem asi dvaceti populárních knih, z nichž hezká řádka byla přeložena do češtiny a překlady (i originály) budou jistě přibývat. Jejich názvy (Původ vesmíru, Kniha o nekonečnu, Konstanty přírody, Teorie všeho, Teorie ničeho…) budí dojem, že Barrowovo populární dílo pokrývá značně širokou a různorodou problematiku. Dojem je správný. Když ale knihy jen zběžně prolistujeme, můžeme mít pocit, že autor tak trochu šidí, že se opakuje: o rozpínání vesmíru, o Einsteinově obecné teorii relativity, o teoriích velkého sjednocení, o antropickém principu, o úloze konstant a dalších tématech se dočteme hned v několika jeho knihách.

To je ale v pořádku. Různé oblasti fyziky a kosmologie jsou navzájem tak propojené, že prostě není možné nezmínit se o historii vesmíru, když se mluví o teoriích velkého sjednocení, opomenout fyziku částic, mluvíli se o temné hmotě, přeskočit obecnou teorii relativity při popisu vesmíru ve velkých měřítkách. Například k velkému sjednocení základních sil má docházet při vysokých energiích, které existovaly v raném vesmíru. Na každé konferenci o fyzice elementárních částic je dnes značná část příspěvků věnována kosmologii, raný vesmír je jediná laboratoř, jež dovoluje testovat teorie částic při extrémně vysokých energiích. Jen sama otázka, zda kosmologie je součástí fyziky, nebo fyzika podoblastí kosmologie, představuje látku na delší esej.¹⁾

Učitelům na všech úrovních působí tato provázanost komplikace, když se pokoušejí výklad o kosmologii uspořádat. Na vědecké úrovni se předpokládá, že než se začne student věnovat kosmologickým otázkám, projde rozsáhlým kurzem fyziky a kvantové teorie. To ale není přijatelné pro popularizátora. Barrow to řeší tím, že jeho knihy nás vedou po naučných stezkách, jež mají určitý leitmotiv. Stezky se kříží, proplétají a na ty nejvýznačnější přírodní památky narazíme hned na několika z nich. Jenže k nim přicházíme z různých stran, takže jde vždy o nový zážitek, jinou perspektivu.

Barrow jako zkušený průvodce výklad také citlivě koření legendami spojenými s tématem a uvádí řadu literárních citátů a historek o vědcích. Vypráví-li je aktivní badatel, který se s mnohými protagonisty příhod osobně zná, je to nejen oživení, ale i pohled do zákulisí, jak se věda dělá.

Napsal jsem, že čtenář vidí problém z různých perspektiv. Spíše se však setkává s obrazy, které autor vytvořil pomocí příkladů a analogií. Popularizátor, který se snaží přiblížit fyzikální teorii, je v nezáviděníhodné situaci kunsthistorika, který provádí po galerii nevidomého, nebo hudebního vědce, který seznámuje s krásami Beethovenovy tvorby neslyšícího. Je mu totiž odepřeno používat při výkladu výrazového prostředku, pomocí kterého jsou díla vytvořena, v případě fyziky tedy matematiky. Užívá proto obrazů, ty ale nejsou nikdy zcela věrné.

Grafy a vyobrazení k výrazovým prostředkům vědy patří a pro laického čtenáře jsou přece jen přístupnější než matematické vzorce. Grafy jsou důležitým prostředkem k přehlednému zachycení výsledků měření. A některé obrázky a diagramy vědou doslova pohnuly. O tom nás přesvědčí další do češtiny přeložená Barrowova naučná stezka nazvaná Vesmírná galerie.

Nese podtitul Klíčové obrazy v dějinách vědy, a to – řečeno autorovými slovy – obrazy, z nichž každý vypráví příběh. Spolu s výstižným úvodem je na stezce celkem 90 zastavení čtyř tematických okruhů, zastavit se tedy můžeme jen u některých.

Úvodní tematický okruh s poetickým názvem Hvězdy v tvých očích pojednává o obrazech souvisejících s hvězdami a vesmírem. Hned na prvním zastavení se dozvíme o původu souhvězdí a jejich názvů. Čtenáři asi tuší, že většina jmen je z řecké mytologie a jakou roli hrají v astrologii. Ne všichni ale vědí o dnešní diskrepanci mezi skutečnou polohou Slunce a astrologickým zvěrokruhem, kterou způsobila precese zemské osy, a možná plně nedoceňují význam, který měla hvězdná obloha pro orientaci mořeplavců. Řada nádherných uměleckých zpracování noční oblohy v autorově výběru dokumentuje, jak v průběhu věků hvězdné nebe lidi fascinovalo.

Ale rychle dále, v této části je toho k vidění ještě mnoho. Pomiňme krásné fotografie mlhovin a galaxií, význam Hubbleova diagramu pro důkaz expanze vesmíru, spektrum mikrovlnného záření a další témata a zastavme se u toho, jak vhodný diagram skutečně pohnul vědou. Necelé tři roky poté, co Einstein předložil svou speciální teorii relativity, přišel Hermann Minkowski s představou čtyřrozměrného prostoročasu. Fyzikálně nedodávalo toto pojetí k Einsteinově teorii nic nového, ale umožnilo mnohem elegantnější matematický zápis. A hlavně vedlo k znázornění pomocí „prostoročasových diagramů“, jež dovolovaly snadno interpretovat takové důsledky teorie relativity, jako je prohození časového sledu událostí v různých systémech či kontrakce délek. Jasně demonstrují i to, proč relativita času nevede ke kauzálním paradoxům, je-li rychlost světla tou nejvyšší rychlostí, kterou se mohou šířit informace. A byla-li představa prostoročasu pro speciální teorii relativity užitečná, pak pro největší Einsteinovo dílo, obecnou teorii relativity, popisující gravitaci jako zakřivení prostoročasu, je prostoročasový popis naprosto nezbytný. Představit si zakřivení prostoročasu ovšem není snadné, a to ani pro matematicky zběhlé vědce. I zde vtipné diagramy sehrály význačnou roli v rozvoji teorie.

Richard Feynman líčí, jak se chtěl za studií seznámit s anatomií kočky a šokoval knihovnici, když ji požádal o „mapu kočky“. S takto volněji pojatým slovem „mapa“ můžeme říci, že druhý tematický okruh se věnuje mapám. Opravdu tam nalezneme hodně o zobrazování zemského povrchu, o geologických a meteorologických mapách, ale také o snímcích Země z družic, o kanálech na Marsu, obrázcích zatmění Slunce, poselství mimozemšťanům v sondách Pioneer i o Vesaliově anatomické „mapě“ lidského těla. K tomuto oddílu se však zachovám macešsky a přejdu k třetímu okruhu, který se týká především „čisté“ matematiky.

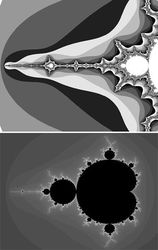
Obrázky mají v matematice zvláštní postavení. Na jedné straně je obrázek v matematické argumentaci většinou nepřípustný důkazní prostředek; student, který by při zkoušce z matematické analýzy prohlásil, že platnost nějaké věty je patrná z obrázku, by neuspěl. Věta musí být dokázána přesnou logickou argumentací jako důsledek určitých předpokladů – právě v tom je pro zasvěcence jedno z kouzel matematiky. Na druhé straně si ovšem i nejabstraktnější matematik obrázkem zpravidla zviditelňuje obsah nějakého tvrzení na typickém příkladu. A jsou oblasti matematiky, jež se zabývají právě teorií zobrazování, a v některých matematických disciplínách hrají obrázky zásadní význam. V tomto oddíle nás autor seznámí s platonskými tělesy, s Erathostenovým sítem na hledání prvočísel (viz Vesmír 72, 605, 1993/11), s Möbiovou páskou, jež má jen jednu stranu, se zobrazováním vyšších dimenzí či s poměrně moderní disciplínou, jakou je teorie fraktálů. Určitý útvar má fraktálovou strukturu, je-li „samopodobný“, určitý motiv se opakuje, pozorujeme-li objekt v jakémkoli měřítku. Co se tím míní, vidíme například na takzvané Mandelbrotově množině (obr. 1). Fraktály jsou vděčné v tom, že umožňují počítačově vytvářet artefakty s podivuhodným estetickým kouzlem. Takové struktury ovšem nacházíme i v přírodě nebo třeba na obrazech Jacksona Pollocka malovaných „rukou“. Abstraktní matematika má řadu aplikací a souvisí s nejrůznějšími oblastmi lidské činnosti. Jedeme- -li metrem, moc nás nezajímá, pod čím právě projíždíme, a tedy ani přesné zakreslení trati do plánu města. Potřebujeme ale vědět, jak stanice následují za sebou a kde se linky kříží. Z toho vycházel Harry Beck, když v roce 1931 nakreslil schéma londýnské podzemní dráhy, jež se pro svou přehlednost stalo vzorem pozdějších podobných schémat. Tímto příkladem nás Barrow nechává nahlédnout do velmi abstraktní matematické disciplíny zvané topologie (oboru, ke kterému významně přispěli čeští matematici).

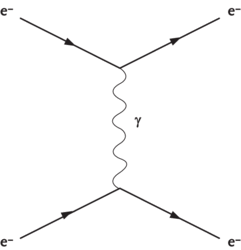
Poslední oddíl Duch nad hmotou se týká především moderní chemie a kvantové teorie. Dočteme se o benzenovém jádře, struktuře DNA, atomovém hřibu, Schrödingerově kočce a dalších tématech. Kekulého šestiúhelníky a dvojitá spirála jsou určitě příklady schémat, která výrazně posunula organickou chemii či molekulární biologii. To však je mému zaměření dosti vzdálené, a tak mé poslední zastavení bude u takzvaných Feynmanových diagramů, které jsou skvělým příkladem toho, jak obrázky způsobily průlom ve vědě.

Kvantovou elektrodynamikou se rozumí kvantová teorie vzájemného působení nabitých částic. Za své práce na toto téma z konce čtyřicátých a počátku padesátých let dostali v roce 1965 Sin-Itiro Tomonaga, Julian Schwinger a Richard Feynman Nobelovu cenu. Všem třem se podařilo matematicky krásně popsat interakci elektricky nabitých částic a jejich teorie – v podstatě ekvivalentní, jak se později ukázalo – vedly k výsledkům, jež spolehlivě potvrdil experiment. Pracovním nástrojem teoretiků i experimentátorů v částicové fyzice se však stala především metoda navržená Richardem Feynmanem. Ten totiž uspořádal výpočty pomocí série obrázků, které popisují výměnu virtuálních částic. Každý takový graf představuje elementární proces, jenž přispívá k výsledné hodnotě měřitelné veličiny. Grafy mohou být podstatně složitější než ten vyobrazený a je jich nekonečně mnoho (obr. 2). Naštěstí čím složitější diagram, tím menší je jeho vklad do výsledku, proto většinou stačí omezit se na grafy nižšího řádu.

Nějaký Feynmanův diagram viděl snad každý čtenář, který se zajímá o fyziku. Nedejme se však mýlit. Chceme-li z těchto obrázků získat skutečnou experimentálně ověřitelnou informaci, zdlouhavým výpočtům se nevyhneme. Obrázky jsou ale spolehlivým algoritmem, podle kterého můžeme postupovat a jenž nám dává jistotu, že jsme ve výpočtu nic důležitého nevynechali. Bez Feynmanových diagramů si dnes žádný fyzik nedovede kvantovou teorii představit a jejich užitečnost přesahuje kvantovou elektrodynamiku, pro jejíž potřeby vznikly. A pro popularizátory jsou Feynmanovy grafy pravým požehnáním. Představa silového působení prostřednictvím výměny částic je natolik poutavá a Feynmanovy obrázky ji tak pěkně zachycují, že si čtenář ani neuvědomí, kolik toho ještě zbývá ke skutečnému pochopení. Feynmanovo obrázkové písmo lze pokládat za ikonu kvantového popisu interakcí.

Společným rysem velkých obrazových galerií je jejich únavnost. Louvre, El Prado nebo galerii Uffizi neopustí milovník umění proto, že by se nabažil jejich pokladů, nýbrž proto, že protestují nohy a páteř. Má-li však příležitost, přijde znovu. Vesmírná galerie se také těžko prohlédne souvisle, těch příběhů je příliš mnoho. Jsou ale natolik samostatné, že se čtenář může snadno vracet a žádná z návštěv nebude zklamáním – vesmír je plný umění.

Zbývá ohodnotit grafickou výpravnost a překlad Jana Novotného, stylisticky velmi zdatného relativistického fyzika se zájmem o historii a filozofii vědy. Obojímu náleží jednička s velikou hvězdičkou.