Karty, počítače a rekreačná matematika

FreeCell je kartová hra pre jedného hráča (podobne ako pasiáns), ktorú dodáva Microsoft so svojím operačným systémom Windows, vďaka čomu sa stala veľmi populárnou medzi používateľmi počítačov. Napriek presvedčeniu tvorcu softwarovej verzie sa niektoré partie hry nedajú vyhrať, a preto upozorníme na niektoré všeobecnejšie súvislosti medzi matematikou (kombinatorikou), počítačmi a (kartovými) hrami.

Hra FreeCell je variantom hry Forty Thieves (Štyridsať zbojníkov), o ktorej sa traduje, že si ňou Napoleon krátil svoj posledný exil na Svätej Helene. Stala sa populárnou najmä potom, ako ju Microsoft začal distribuovať s prvými verziami operačného systému Windows v roku 1981.

Autor softwaru Jim Horne v inštrukciách ku hre uvádza: Predpokladá sa (hoci bez dôkazu), že každá hra sa dá vyhrať. V tomto článku ukážeme nesprávnosť tohto tvrdenia a predstavíme skupinu, ktorá má rádovo 10¹² nevyhrateľných hier.

Treba však dodať, že z 52! počiatočných rozložení, ktoré sa zo sady kariet dajú vytvoriť, používateľ Windows môže odštartovať iba 32 000 hier. Z korešpondencie z Jimom Hornom sa autor dozvedel, že iba jednu z nich (hru číslo 11 982) sa doposiaľ nikomu nepodarilo vyhrať.

Pravidlá hry

Na hracej doske sa nachádzajú štyri domovské políčka vpravo hore, štyri voľné políčka vľavo hore, a sada kariet v ôsmich stĺpcoch. Karty sú obrátené lícom nahor. Na obrázku je jedno takéto počiatočné rozloženie prevzaté priamo z obrazovky. Cieľom hráča je prekladať karty tak, aby na záver boli všetky v domovských políčkach. Karty v nich musia byť uložené podľa farby (každá farba v jednom domovskom políčku) a podľa veľkosti (od esa po kráľa). Pritom hráč môže počas hry dočasne položiť karty aj na voľné políčka.

Pravidlá hry sú jednoduché. Počiatočné rozloženie kariet je náhodné. Z počiatočného rozloženia sa treba dostať do cieľového štyrmi typmi presunov:

• Presun najspodnejšej karty v stĺpci na voľné pole. Presun sa dá uskutočniť, iba keď je pole prázdne, lebo voľné políčka smú obsahovať len jednu kartu.
• Karta z voľného políčka alebo najspodnejšia karta v stĺpci sa môže položiť pod najspodnejšiu kartu v inom stĺpci. Pritom presun sa môže uskutočniť iba tak, aby karty na dolnom konci stĺpca boli usporiadané podľa veľkosti od najvyššej (kráľ) po najnižšiu (eso). Pritom karta, pod ktorú ukladáme, musí mať hodnotu väčšiu o jeden a opačnú farbu. Napríklad, prvými presunmi na obrázku by mohli byť: presun 9♣ do siedmeho stĺpca pod 10♦ alebo presun 2♣ pod 3♥ a pod.
• Ktorúkoľvek kartu z voľného políčka alebo zo spodu stĺpca možno presunúť do domovského políčka (pričom treba rešpektovať farbu a hodnotu karty). Eso možno presunúť kedykoľvek na prázdne domovské políčko, naň možno postupne klásť vyššie karty tej istej farby. Napríklad na obrázku možno presunúť eso♦ na jedno z domovských políčok – vzápätí nato možno naň položiť 2♦.
• Keď sa niektorý stĺpec vyprázdni, možno doň vložiť ktorúkoľvek kartu z voľného políčka alebo najspodnejšiu kartu niektorého stĺpca.

  Hra je úspešne („víťazne“) ukončená, keď v domovských políčkach sú štyri kompletné postupnosti jednotlivých farieb. Ak hráč nemôže urobiť žiaden legálny presun alebo iba ich cyklickú (donekonečna sa opakujúcu) sériu, hra je prehraná.

Upresnenie základných pojmov

Na začiatku hry sa všetky karty nachádzajú (náhodne rozložené) lícom nahor na vytieňovaných pozíciách na obrázku. Políčka pod nimi (z ktorých sme naznačili iba niekoľko prvých) možno počas hry využiť. Z dôvodov, ktoré budú zrejmé neskôr, delíme hraciu plochu aj na ľavú a pravú časť. Ľavá časť má 7 riadkov, pravá iba 6, čo dohromady poskytuje priestor na položenie všetkých 52 kariet.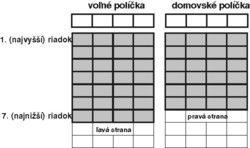

Základné nevyhrateľné postavenie

Najprv ukážeme základné rozloženie a dokážeme, že sa nedá vyhrať. Potom ukážeme sériu transformácií, ktoré zachovávajú nevyhrateľnosť.

Na obrázek je nevyhrateľné rozloženie, ktoré budeme v ďalšom texte označovať ako základné. Ako sa možno ľahko presvedčiť (napríklad aj pokusmi o hru), každý pokus vedie do stratena. My však uvedieme aj formálny dôkaz.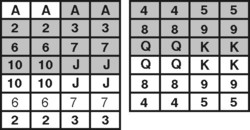

Vzdialenosti kariet a racionálne postupnosti

Teraz dokážeme, že všetky možné postupnosti presunov kariet zo základného rozloženia vždy vedú k pozíciám, v ktorých už neexistujú legálne kroky. Takéto pozície budeme označovať ako zablokovanie. Najprv však uvedieme krátke postrehy, vďaka ktorým vieme dôkaz skrátiť:

• Farba kariet nehrá v dôkaze podstatnú úlohu. Stĺpce 1 a 2, 3 a 4, 5 a 6, 7 a 8 sa očividne dajú považovať za identické. V dôsledku toho pre ľubovoľný z týchto párov stĺpcov stačí iba jeden dôkaz.
• V dôkaze sa obmedzíme na racionálne postupnosti presunov, čiže na také, ktoré nevedú k okamžitému, ľahko predvídateľnému zablokovaniu. Napríklad presun všetkých dvojok a trojok na štyri voľné políčka určite nie je racionálny, nakoľko po tejto sade presunov nie je možný žiaden ďalší ťah. ¹⁾ Inak povedané, racionálna postupnosť musí dovoľovať najmenej jeden presun inde ako do voľných políčok predtým, než dôjde k zablokovaniu.
• Uvažovanú kartu budeme nazývať miestodržiteľ. Väčšina kariet (okrem es a kráľov) má dvoch partnerov: horného suseda a dolného suseda. Horný sused je karta, pod ktorú môžeme miestodržiteľa presunúť. Dolný sused je karta, ktorá sa dá presunúť pod miestodržiteľa. Napríklad horný sused čiernej 5 je každá červená 6 a jej dolný sused je každá červená 4.
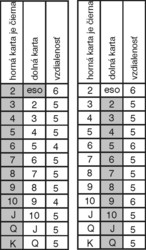
• Na obrázku vidieť vzdialenosti medzi susednými kartami v základnom rozložení. Vzdialenosťou rozumieme minimálny počet kariet, ktoré treba presunúť nato, aby sa dolná karta mohla presunúť pod hornú.

Dôkaz nevyhrateľnosti

Na začiatku sú všetky spodné karty červené. Preto jediný možný ťah je presun karty na voľné políčko. Naviac – pretože len dve vzdialenosti v tabuľke sa rovnajú 4 – existujú iba dve racionálne postupnosti presunov:

• Po presunutí červenej 2, 6 a 10 a čiernej 10 na voľné políčka sa dá červená 5 presunúť pod čiernu 6.
• Po presunutí červenej 2, 5, 6, a 10 na voľné políčka možno červenú 9 presunúť pod čiernu 10.

Červené 2, 6, a 10 s čiernou 10

Keď presunieme červenú 2, 6 a 10 spolu s čiernou 10 na voľné políčka, dá sa aj červená 5 presunúť pod čiernu 6. Situáciu po týchto krokoch vidieť na obrázku.

V danej chvíli neexistuje ani jeden legálny presun. Všetky spodné karty sú červené. Jediná dostupná čierna karta má hodnotu 10 a nachádza sa na voľnom políčku. Nemožno ju však presunúť, nakoľko červené J je zakryté dvomi inými kartami.

Červené 2, 5, 6, a 10

Po presunutí červenej 2, 5, 6 a 10 na voľné políčka možno červenú 9 presunúť pod čiernu 10. Vzniknutú situáciu vidieť na obrázku.

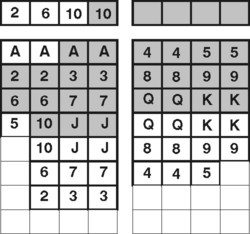To je očividné zablokovanie. Všetky spodné karty a všetky karty na voľných políčkach sú červené. Žiaden ďalší presun karty nie je možný. Pretože žiadne ďalšie racionálne postupnosti neexistujú, týmto je dôkaz úplný.

Modifikácie základného rozloženia

Ostatné nevyhrateľné rozloženia, ktoré uvedieme, odvodíme zo základného rozloženia. Keďže jeho nevyhrateľnosť sme práve dokázali, pri ich tvorbe použijeme iba transformácie, ktoré zachovávajú vlastnosť nevyhrateľnosti. Pochopiteľne vždy najprv uvedieme príslušnú transformáciu, a potom vysvetlíme, prečo zachováva nevyhrateľnosť.

Úloha farby

Doteraz sme hovorili nie o štyroch farbách kariet, ale iba o „čiernej“ a „červenej“. Pretože „červená“ znamená v skutočnosti dve farby (srdce a káro) a čierna tiež, skutočný počet nevyhrateľných rozložení je vyšší.

Počas dôkazu nebolo žiadne eso odkryté. To znamená, že v tomto prípade nie je dokonca podstatné ani to, či je jeho farba červená alebo čierna. V dôsledku toho ktorákoľvek permutácia es v prvom riadku na ľavej strane hracej dosky zachováva nevyhrateľnosť. Esám možno preto „priradiť farbu“ 4!, tj. 24 spôsobmi.

Ak však chceme zachovať vzdialenosti z tabuľky 4, všetky zvyšné karty si musia zachovať príslušnosť k červenej, resp. k čiernej. V tomto prípade máme teda možnosť vykonať 2 × 2 = 4 zmeny pri kartách jednotlivých hodnôt. Teda konkretizáciou farby es a dvanástich ostatných kariet získavame

M = 24 × 4¹² = 402 653 184

rozličných nevyhrateľných rozložení (s tým istým rozložením hodnôt ako na obrázku).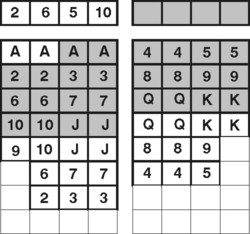

Úloha stĺpcov

Stĺpce sa tiež dajú presunúť bez újmy na nevyhrateľnosti. Treba ich však vymeniť ako celky, aby sa farby nepomiešali – s dôsledkami pre platnosť dôkazu.

Predovšetkým, aby sme manipuláciu zjednodušili, „odstránime“ riadok so štyrmi esami. (V skutočnosti ho ponecháme presne tam, kde je, ale pri výmenách ho nebudeme brať do úvahy.) Tým (zdanlivo) získame 8 stĺpcov, každý so šiestimi kartami (pozri obrázek). Ak stĺpce presunieme ako celky, vzdialenosť medzi kartami sa nemôže zmeniť. Vďaka tomu dôkaz ostane v platnosti.

Pochopiteľne niet najmenšieho dôvodu vymieňať stĺpec, ktorý začína dvojkou, s iným stĺpcom, ktorý ňou tiež začína. Rovnaký argument platí pre všetky páry stĺpcov, ktoré začínajú rovnakými hodnotami. Preto počet „zmysluplných“ výmen stĺpcov je 8!/2⁴ = 2520. Keďže každé nové rozloženie môžeme zafarbiť podobne ako základné, po tejto úprave poznáme

N = 402 653 184 × 2520 = 1 014 686 023 680

rôznych nevyhrateľných rozložení.

Dodajme, že výmena pásov červených a čiernych kariet na obrázku nemôže ovplyvniť platnosť dôkazu (iba symetricky modifikovať tabuľku 4). Z toho vyplýva, že celkový počet rozložení, ktoré sa dajú priamo generovať zo základného, je

2 × N = 2 029 372 047 360.

Uvedená úloha je typickou úlohou z oblasti rekreačnej matematiky. Nie je to abstraktný matematický problém, ale problém zábavný, jednoducho formulovateľný, ktorého riešenie však zároveň vyžaduje istú erudíciu a formálne postupy. Konkrétne:

• Definovanie nových pojmov, ktoré zjednodušia a sprehľadnia riešenie (miestodržiteľ, horný a dolný sused, vzdialenosť kariet, …).
• Formulovanie tvrdení a ich dôkaz (napr. nevyhrateľnosť základného rozloženia).
• Zovšeobecnenie tvrdení (vytvorenie triedy nevyhrateľných hier).

Úlohy z rekreačnej matematiky sú teda vlastne rovnako dobrým nástrojom na budovanie matematického poznania ako úlohy čisto formálne, ktorými sa získavajú nové matematické výsledky. Samotné riešenie však nie je triviálne, lebo si vyžaduje dôkladne sa oboznámiť s problémom (odohrať prinajmenšom niekoľko desiatok hier), formálne uvažovať (odhaliť stratégiu, ako narúšať „vyhrateľnosť“) a nepostrádať schopnosť abstrakcie (napríklad ignorovať faktory, ktoré na víťazstvo alebo prehru nemajú vplyv).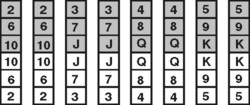

Vzhľadom na svoj zábavný charakter úlohy z rekreačnej matematiky môžu dokonca prinášať pri vyučovaní matematiky aj lepšie výsledky ako klasické, pretože sú pre žiakov atraktívnejšie. Autor má prinajmenšom zo svojho nového pôsobiska tento pocit.