O vážení neutrin a nepoctivém prodavači podivných jablek
| 5. 2. 1994Odpověď na zdánlivě prostou otázku, jakou hmotnost mají neutrina, představuje jednu z největších záhad současné fyziky elementárních částic. Dříve, než se zmíníme o nejnovějších výsledcích „vážení“ neutrin, připomeneme ve stručnosti, jakou roli ve fyzice částic vlastně hmotnosti hrají a proč právě znalost hmotnosti neutrin je tak důležitá. Budeme se pohybovat v rámci tzv. standardního modelu interakcí elementárních částic, jenž, aspoň podle všech dnes dostupných experimentálních dat, velice dobře popisuje zákonitosti mikrosvěta, tj. struktury a interakci hmoty na vzdálenostech menších, než je zhruba velikost protonu. A ten je podle našich běžných měřítek velice malý: na 1 milimetr se vejde milion milionů protonů seřazených těsně vedle sebe! Zvolil jsem úmyslně výraz „popisuje“, neboť tento model obsahuje řadu volných parametrů, jejichž konkrétní hodnoty je nutno určit z experimentu. Ty pak ovšem rozhodují nejen o vlastnostech elementárních částic a jejich vzájemného působení, ale i o strukturách daleko větších, od chemických sloučenin až po vesmír jako celek. Tyto parametry jsou v podstatě dvojího druhu:
- vazbové konstanty interakcí částic, tedy veličiny příbuzné elektrickému náboji, jenž určuje velikost elektromagnetických sil,
- hmotnosti základních částic.
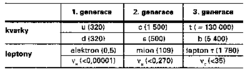 Na tomto místě je patrně vhodné připomenout základní objekty, s nimiž standardní model pracuje a které tedy dnes považujeme za „elementární“. Jsou shrnuty v tab. I vlevo dole (νe, νμ, ντ označují elektronová, mionová a tau neutrina).
Na tomto místě je patrně vhodné připomenout základní objekty, s nimiž standardní model pracuje a které tedy dnes považujeme za „elementární“. Jsou shrnuty v tab. I vlevo dole (νe, νμ, ντ označují elektronová, mionová a tau neutrina).
Tab. I seskupuje všechny částice, jež dnes považujeme za elementární, do tří generací. Každá generace je složena ze dvou kvarků a dvou leptonů, přičemž jediným pozorovatelným rozdílem mezi odpovídajícími částicemi různých generací jsou právě jejich hmotnosti, všechny ostatní charakteristiky jsou naprosto stejné pro všechny generace! Důvod, proč v přírodě dochází k takovému opakování základních struktur hmoty je nám dosud utajen a představuje jednu z ústředních otázek současné fyziky částic.
I když tedy nevíme proč, poslední experimenty v Evropském středisku fyziky částic (vzhledem k tomu, že obsah samotného pojmu „elementární částice“ se v souvislosti s postupujícím stupněm poznání mikrosvěta přirozeně neustále mění, používá se dnes obvykle pro označení tohoto oboru pouze název „fyzika částic“) CERN u Ženevy odpověděly na otázku, kolik takových různých generací existuje: vše nasvědčuje tomu, že pouze tři, a tedy že naše tabulka vyčerpává všechny v přírodě existující elementární fermiony. Při pohledu na ni nás ovšem zarazí skutečnost, že zatímco všechny kvarky a nabité leptony mají dosti přesně určenou nenulovou hmotnost, u neutrin nacházíme jen horní hranici jejich hmotnosti. A skutečně, i když elektronové neutrino známe už téměř 40 let, mionové 30 a neutrino tau 17 let, neumíme zatím přesvědčivě odpovědět na základní otázku, zda neutrina jsou nehmotná (jako např. foton), nebo zda mají nenulovou hmotnost a jakou.
Srovnání s fotonem jsem uvedl úmyslně, neboť se tím dostáváme k druhé skupině částic, jež se v současné době považují za elementární. Jde o tzv. zprostředkující bozony, což jsou částice zcela jiné povahy než fermiony z předchozí tabulky. Mají spin 1 (a proto se jejich soubory řídí Boseho-Einsteinovou statistikou, tj. neplatí pro ně Pauliho vylučovací princip jako např. pro elektrony). Ty, které vystupují ve standardním modelu, jsou uvedeny v tab. II. Hrají také jinou roli než fermiony. Jsou to objekty, které, jak název naznačuje, „zprostředkovávají“ různá silová působení mezi kvarky a leptony.
Trochu zjednodušeně si lze toto zprostředkování představit asi tak jako působení mezi dvěma loďkami, jejichž posádky si mezi sebou házejí míč a tím se vzájemně odpuzují. Váha míče odpovídá hmotnosti příslušného zprostředkujícího bozonu a je také jasné, že čím těžší míč, tím méně s ním dohodíme, a tedy tím „kratší“ je i dosah sil. S fotonem, jenž zprostředkuje elektromagnetické síly, a také s gluony, jež zprostředkují silné interakce, „dohodíme“ do nekonečna, zatímco s bozony označovanými W+, W-, Z0, jež mají poměrně značnou hmotnost, jen asi do vzdálenosti jedné desetitisíciny průměru protonu.
Nehmotnost fotonu i gluonu není přitom náhodná, ale je to fakt zásadní důležitosti, vyplývající z požadavku jisté symetrie. Nebudeme se zde touto tzv. kalibrační symetrií podrobněji zabývat, chci jen podtrhnout, že postulát této symetrie představuje snad nejdůležitější pilíř dnešní teorie elementárních částic, a proto v tomto smyslu nehmotnosti fotonu a gluonu „rozumíme“.
Zcela jiná je ovšem situace v případě neutrin. U nich na jedné straně zatím nemáme žádné přesvědčivé svědectví, že jejich hmotnost je nenulová, ale ani neznáme nějaký princip či symetrii, která by naopak nehmotnost vyžadovala (jako v případě fotonu).
Je ovšem vůbec důležité na tuto otázku znát odpověď? A jestliže ano, proč? Závažnost otázky se projevuje ve třech okruzích problémů:
- Vnitřní konzistence standardního modelu: V rámci standardního modelu je obtížné připustit neutrina s přesně nulovou klidovou hmotností společně s hmotnými kvarky a nabitými leptony. Touto otázkou se nebudeme dále zabývat.
- Problém nedostatku slunečních neutrin: Již po více než dvě desetiletí se měří toky elektronových neutrin ze Slunce, které v něm vznikají jako produkty fúzních procesů. Na základě našich představ o průběhu těchto procesů byl již před mnoha lety spočten tok slunečních neutrin, který by měl dopadat na Zemi. Skutečně změřený tok představuje jen asi 1/3 předpovězené intenzity. I když je možné, že aspoň část tohoto rozdílu jde na vrub naší nedostatečné znalosti slunečních procesů, většina odborníků je toho názoru, že hlavní příčina je jinde.
- Astrofyzikální souvislosti: Neutrina sehrála důležitou roli v raném stadiu vesmíru, a protože podobně jako fotony i ona „přežila“ do současné doby v hojném počtu a mohou tak výrazně přispět k dnešní hustotě hmotnosti ve vesmíru. Neutrina s nenulovou klidovou hmotností by mohla hrát roli tzv. temné hmoty ve vesmíru (tj. hmoty, kterou přímo nepozorujeme, ale o jejíž přítomnosti máme nepřímé svědectví). Příliš těžká standardní neutrina by byla ovšem v rozporu s pozorovanou mírou rozpínání vesmíru. Pokud je ve vesmíru tolik neutrin, kolik očekáváme, astrofyzikové by vítali neutrina s hmotností v oblasti desítek elektronvoltů. Při takové hmotnosti neutrin by náš vesmír byl uzavřený a neutrina by hrála důležitou roli při tvorbě galaxií.
Nyní, když už nemáme pochyb, že „vážení“ neutrin je věc velice záslužná, podívejme se na to, jak se vlastně provádí. Nejde pochopitelně o vážení tak, jak jsme na ně zvyklí z každodenního života, ale – podobně jako u vesmírných objektů – jde o měření nepřímé, spočívající v detekci průvodních jevů. U neutrin je navíc ještě komplikace v tom, že jsou nejen elektricky neutrální, takže je nelze zakřivovat v magnetickém poli (což je běžný způsob stanovování hmotnosti elektricky nabitých subatomárních částic), ale také velice slabě interagující s ostatními částicemi.
Používaný způsob se proto opírá o detekci a měření jiných, obvykle nabitých částic, s nimiž si víme lépe rady. Typickým příkladem je rozpad volného neutronu, probíhající podle schématu: neutron → proton + elektron + antineutrino. V něm lze v principu z měření energie vzniklého elektronu určit na základě zákona zachování energie a hybnosti hmotnost elektronového neutrina (hmotnosti neutrina a antineutrina jsou stejné), jež v rozpadu rovněž vzniká. Ze zákona zachování energie a hybnosti plyne pro energii vyletujícího elektronu jistá maximální hodnota Emax = E (m(νe)), která ovšem přirozeně závisí na hmotnosti m(νe) doprovázejícího antineutrina: čím těžší je neutrino, tím méně kinetické energie zbývá na produkty rozpadu, a tedy i na elektron.
Touto metodou byla do dnešního dne stanovena horní hranice hmotnosti νe, asi 10 eV. Horní hranice hmotnosti mionového neutrina a neutrina tau byly určeny, ovšem s menší přesností, z podobných rozpadů, jako např. π+ → μ+ + νμ p+ m+ + nm, jenž je převládajícím způsobem rozpadu mezonu p. Existuje i analogický rozpad s produkcí elektronového neutrina: π+ → e+ + νe.
Oscilace neutrin
Kromě této, dnes už klasické metody „vážení“ neutrin existuje ještě jedna, která byla navržena asi před 20 lety a která se opírá o velice zajímavý efekt kvantové povahy, nazývaný „oscilace“ neutrin. Přesto, že jde o typicky kvantový jev, lze ho, samozřejmě za cenu určitého zjednodušení, pochopit na následující analogii s takovou celkem všední záležitosti, jako je návštěva u zelináře.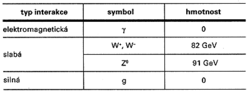
Ještě dříve, než se k němu vydáme, připomeneme, že hmotnost je jednou ze základních charakteristik všech částic, ať už jde o částice mikrosvěta nebo o objekty každodenního života. Každá částice by podle našich představ tedy měla mít nějakou určitou hmotnost, kterou sice nemusíme přesně znát, ale kterou tato částice "má". V kvantovém světě ovšem tato „samozřejmost“ neplati, což má mimořádné důsledky. V kvantové mechanice totiž existují i stavy částic, jež nemají klasické protějšky. Jedná se o lineární superpozice tzv. „čistých“ stavů, tedy stavů, které mají zcela určité (byť kvantované) hodnoty různých fyzikálních veličin, např. právě hmotnosti. „Jisté“ stavy tedy stále odpovídají naší vžité představě, že částice mají své „dobře“ definované vlastnosti, jako je hmotnost a podobně. U lineárních superpozicí však klasické představy selhávají.
Abychom si ozřejmili, v čem je problém, pojďme nyní na nákup k zelináři a kupme si třeba jedno z krásných velkých jablek v ceně 20 Kč/kg. Na váze vidíme, že má právě 1/4 kila, ale zelinář na nás přesto chce 7,50. Těžko bychom asi v tomto případě přijali jeho vysvětlení, že sice váha udává čtvrt kila, ale že to je jen náhoda, neboť totéž jablko mohlo vážit také půl kila. A proto že nám tedy účtuje střední hodnotu z obou cen: 7,50 = (5+10)/2. K takovému nepoctivému zelináři bychom asi už nešli a chuť na jeho podivná jablka si raději nechali zajít. A přitom se tato podivná jablka chovají právě tak jako naše neutrina!
Onen zelinář ostatně ani nebyl nepoctivý, měli jsme vlastně jen smůlu, že jsme si chtěli koupit jen jedno jablko. Kdybychom totiž přišli ještě jednou, viděli bychom, že jeho navlas stejná jablka skutečně někdy váží 1/4 a někdy 1/2 kila, a že tedy při větším počtu jablek je jeho “střední“ cena spravedlivá! A tak je tomu i s neutriny. Částice, nebo snad lépe „stavy“, které vznikají při výše zmíněných rozpadech mezonu π (označené νe, νμ; pro jednoduchost zapomeneme na chvíli na třetí neutrino ντ) se chovají jako naše podivná jablka: nemají „dobře definovanou“ hmotnost, ale jsou popsatelné pomocí lineární superpozice „čistých“ stavů ν1, ν2 s dobře definovanými hmotnostmi M1, M2 (to jsou analogy našich 1/4 a 1/2 kil).
Uvedené „míchání“ neutrin ν1, ν2 na νe a νμ je tak popsáno jediným volným parametrem α, nazývaným směšovací úhel. Jeho hodnotu neumíme určit z teorie, a proto je třeba ji určit z experimentu. Hodnota α = 0 odpovídá nulovému míchání, a tedy případu, že neutrina vznikající v rozpadech π již mají určitou hmotnost.
Poznamenejme ještě, že případ M1 = M2 je rovněž nezajímavý, neboť pak i stavy νe, νμ mají určitou hmotnost, a navíc tyto stavy jsou na sebe „kolmé“, tj. nemohou jeden na druhý přecházet. Zavedení neutrin ν1, ν2 je pak vlastně zbytečné. Pozorovatelné důsledky případu M1 ≠ M2, α ≠ 0 jsou v zásadě dvojí. Podívejme se nejprve na to, jak ovlivní již popsanou metodu „vážení“ neutrina νe pomocí měření energie elektronu v β-rozpadu neutronu či tritia. Pozorované spektrum bude mít o trochu nižší sklon než v případě, že se neutrina nemíchají (pro případ, že směšovací úhel α = 0).
Tvar jednoho spektra je znázorněn např. na 73, 65, 1994/2. Příměs ν2 se projeví jako malý zlom na křivce spektra. Protože většina experimentů měřících hmotnost neutrin se soustředila především na koncovou část spektra, nebyly jejich negativní výsledky v přímém rozporu s nedávnými a po pravdě řečeno překvapivými výsledky skupiny kanadských fyziků, kteří pomocí právě popsané metody došli k závěru, že v elektronovém neutrinu je malá (asi 1 %) příměs neutrina s hmotností asi 17 keV! Pokud by se tento jejich výsledek potvrdil, mělo by to pro fyziku částic i astrofyziku dalekosáhlé důsledky. Najít pro tak těžké neutrino místo v našem chápání mikrosvěta a vesmíru, by sice nebylo jednoduché, ale právě neočekávané objevy často vedou k zásadnímu pokroku.
Bohužel (či bohudík?), jak vyplývá z předchozího příspěvku, situace je prozaičtější, a tak vážení neutrin pokračuje.
Symbolicky
νe = A ν1 + B ν2,
νμ = C ν1 + D ν2,
kde parametry A, B, C, D určují















