Když matematici stěhují pohovku

Stěhování velkých kusů nábytku je úkol, se kterým se jednou za čas musí popasovat každý z nás. Snad právě tato zkušenost navedla v roce 1966 australsko-kanadského matematika Lea Mosera k formulaci tzv. moving sofa problem, neboli problému stěhování pohovky. Zadání je zdánlivě jednoduché: jaký je největší rovinný útvar, který lze přenést pravoúhlou zatáčkou v chodbě o šířce 1?

Stěhování Gerverovy pohovky. Objekt o větší ploše by už přes roh neprošel.

Ilustrace Baek J., 2024

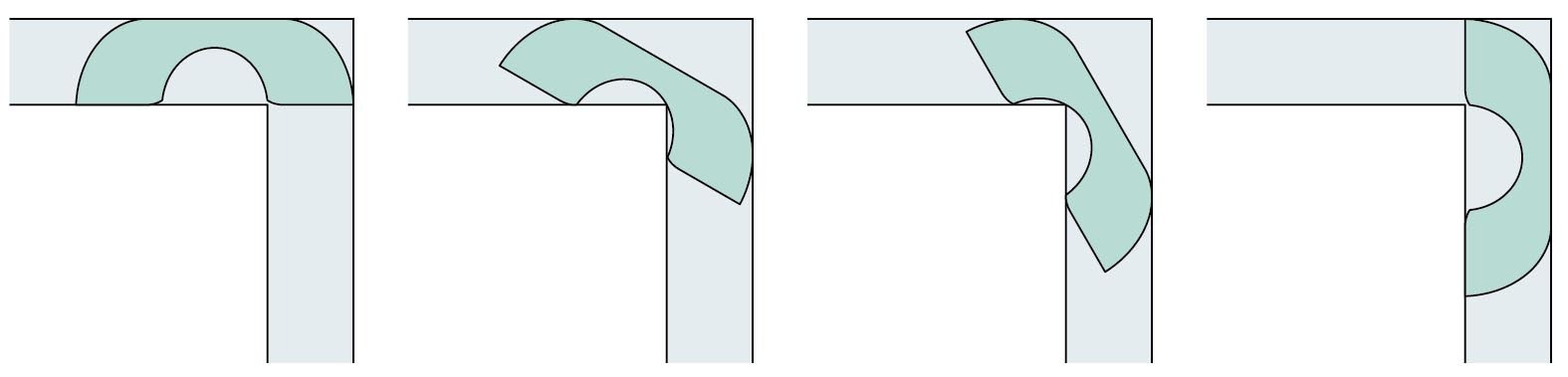
Nejjednodušším příkladem takové pohovky je čtverec o straně 1, tedy i ploše 1. Pokud však využijeme možnost nábytek během průchodu zatáčkou otáčet, dostaneme skrz i půlkruh o stejném poloměru, jehož plocha je přibližně 1,74.

Matematici však tuto hranici posouvali stále dál. Netrvalo dlouho a došli k tomu, že největší pohovky budou mít tvar podobný telefonnímu sluchátku. Největší dosud známá pohovka tento tvar splňuje a nese jméno svého objevitele – Gerverova pohovka. Objevena byla v roce 1992, skládá se z osmnácti sekcí popsaných různými křivkami a její plocha činí přibližně 2,2195. Na druhé straně byla v roce 2018 určena dosud nejpřísnější horní mez: žádná pohovka nemůže mít plochu větší než 2,37.

V prosinci loňského roku publikoval Jineon Baek, postdoktorand z Univerzity Jonse v Soulu, práci, v níž předkládá důkaz, že Gerverova pohovka je skutečně největší možnou. Práce zatím neprošla peer-review procesem. Matematickou veřejnost už ale zaujala originální kombinací vzdálených oblastí matematiky spolu s tím, že nikde nevyužívá počítač jako výpočetní nástroj. Důkaz tak lze provést „po staru na papíře“, což už nebývá běžné. Dnes 75letý J. L. Gerver, autor dosud největší pohovky, se podle časopisu Quanta Magazine vyjádřil, že má velké štěstí, že byl problém vyřešen ještě za jeho života.

Baek J.: arXiv, 2024, DOI: 10.48550/arXiv.2411.19826