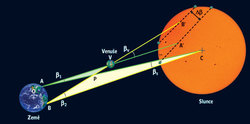
Přechod Venuše před Sluncem

...Průchody tyto opakují se vždy po dvou při každém více než stoletém oběhu její, t. j. po průchodu prvém následuje v osmi letech průchod druhý. Poslední dva děly se 5. června 1761 a 3. července 1769 a byly pozorovány ode všech téměř hvězdářů, neboť juž na počátku osmnáctého století upozornil na ně slavný astronom Halley, jakožto na nejsnadnější a nejzevrubnější prostředek k určení vzdálenosti slunce od země. A což pak dosud neznáme tuto vzdálenost?

Ovšem, známe ji, ale jen podle různých výpočtů dosti značně mezi sebou se lišících, tak že bedlivé opravy jejich nesrovnalosti nezbytně je potřeba.

Toto můžeme číst o přechodu Venuše před Sluncem na druhé straně prvního čísla Vesmíru z 3. května 1871. Přechody Venuše před slunečním diskem 9. prosince 1874 a 6. prosince 1882 byly již několik let před úkazem netrpělivě očekávány jako příležitost odstranit rozpory, které do astronomie vnesly záznamy jezuity Maximiliana Hella (1720–1792) pořízené v Laponsku během předchozího přechodu Venuše. Dosud není jasné, zda se Hell stal obětí svého omylu, nebo zda údaj zfalšoval s úmyslem oklamat vědeckou veřejnost. Záznamy jeho měření byly objeveny až dlouho po jeho smrti v knihovně barona E. F. J. von Munch-Bellinghausena. Původní výsledky pozorování byly přeškrtány a nahrazeny chybnými čísly. Hell, který měl ve své době značnou vědeckou autoritu a jehož výsledky se desítky let neodvážil nikdo zpochybnit, tak způsobil na dlouho zmatek v představách lidí o vesmíru.

Proč je určení astronomické jednotky, tj. střední vzdálenosti Země od Slunce, tolik důležité a ovlivňuje řadu vesmírných vzdáleností? Pro tento jev se v astronomické literatuře vžilo označení „kosmický žebřík“. Spočívá v tom, že určení vzdálenosti ke zkoumanému objektu využívá naši znalost o objektech bližších. Určená vzdálenost je pak východiskem k dalšímu kroku a ke kalibraci našeho měřítka do vzdálenější části vesmíru. Musíme ovšem kalibrovat vzdálenost k první příčce vesmírného žebříku v měřítku naší sluneční soustavy. Třetí Keplerův zákon nám jednoduchou rovnicí svazuje poloosy drah planet a jejich oběžné doby. Známe-li poloosu jedné planety a oběžné doby, můžeme určit vzdálenosti ostatních planet od Slunce a rozměry sluneční soustavy. Pokud známe velikost astronomické jednotky, určují trigonometrické roční paralaxy vzdálenosti k nejbližším hvězdám. Ty vstupují do kalibrace dalších metod pro určení vzdáleností v naší galaxii a v mezigalaktickém měřítku. Přesnost našeho měřítka však závisí na tom, jak přesně změříme první úsek ve sluneční soustavě.

Klíčovou roli astronomické jednotky pro stanovení ostatních vzdáleností ve sluneční soustavě si astronomové uvědomili již v 17. století, brzy po objevu Keplerových zákonů. Kepler také předpověděl přechod Merkura před Sluncem 7. listopadu 1631 a přechod Venuše 7. prosince 1631, avšak sám se těchto úkazů nedožil. Přechod Venuše pozoroval anglický pastor Jeremiah Horrock.

Ten stanovil vzdálenost Země od Slunce na 94 000 000 km, tedy o plných 55 587 000 km menší, než odpovídá skutečnosti. Na přesnosti jeho měření se ovšem podepsalo i to, že kvůli svým církevním povinnostem nemohl pozorovat celý úkaz.

Díky dokonalejším přístrojům a měřením z více navzájem vzdálených míst se zlepšovala i přesnost astronomické jednotky vypočtené při dalších přechodech Venuše. Hodnota astronomické jednotky, kterou vypočetli Alexandre-Gui Pingré a James Short z přechodu v roce 1761, byla nižší „jen“ o 7,4 % a výsledek, k němuž dospěli A.-G. Pingré a Joseph Jérôme Lefrançois de Lalande na základě údajů o přechodech v letech 1761 a 1769, nadhodnotil tuto vzdálenost jen o 1 %. Simon Newcomb se r. 1890 přiblížil k správné hodnotě astronomické jednotky již na pouhých 0,05 %. „Dobrodružství poznání“ však bylo spojeno s opravdovým dobrodružstvím, které někteří astronomové zaplatili životem. Protože jsou pro výpočet astronomické jednotky potřebná pozorování z lokalit vhodně rozmístěných po zeměkouli, dostávaly se anglické a francouzské expedice do míst tehdy pro Evropany nebezpečných a neznámých. Francouzskou expedici astronoma Jeana Chappeho r. 1769 do Mexika nepřežila většina účastníků kvůli epidemii tyfu. V témže roce decimovali zčásti bouře a zčásti lidojedi anglickou tichomořskou expedici kapitána Jamese Cooka. Newcombův vynikající výsledek byl založen na pozorování přechodu z mnoha vědeckých misí.

Ve 20. století byly vzdálenosti k nejbližším planetám změřeny pomocí radarů s přesností na metry. Proč byl tedy r. 2004 organizován rozsáhlý mezinárodní projekt zaměřený na pozorování přechodu Venuše, když máme astronomickou jednotku určenou přesnějšími metodami? Tento celoevropský projekt měl především vzdělávací cíle. Měření úkazu trvajícího 7 hodin a 20 minut se účastnily tisíce pozorovatelů a ke zpracování do Paříže zaslaly více než 4500 zaznamenaných časů dotyků kotoučku Venuše (dvou dotyků vnitřních a dvou vnějších) s okrajem slunečního disku. Astronomický ústav AV ČR byl jedním ze čtyř organizátorů projektu (spolu s Evropskou jižní observatoří, Pařížskou observatoří a Evropskou asociací pro vzdělavání v astronomii při EU), jeho zástupci pracovali v Mezinárodním řídícím výboru projektu a ondřejovská observatoř byla jedním z míst, odkud profesionální astronomové dodávali v přímém přenosu pozorování do sítě internetu. Čeští studenti byli nejaktivnější a v počtu škol zapojených do projektů předstihli i země s několikrát větším počtem obyvatel, například Německo a Francii.

Četnost pozorování a jejich velmi rychlé zpracování kontrastují s těžce získanými měřeními badatelů v 17. a 18. století. Značné problémy jsou však se zpracováním amatérských dat bez znalosti původu a přesnosti. Do Paříže byly zaslány například okamžiky prvního a druhého dotyku určené v Americe v místech, kde Venuše v té době nebyla pozorovatelná. Zřejmě šlo o špatně určené souřadnice místa pozorování.

Jak obstáli amatérští astronomové 21. století v porovnání s vědci předchozích století? Přesnost jejich měření byla rozhodně vyšší, než organizátoři projektu očekávali. On-line výpočet, který dokumentoval statistický efekt počtu měření již během přechodu, se po započtení 4367 měření zastavil na hodnotě lišící se od správné hodnoty astronomické jednotky o pouhých 68 186 km, tj. 0,045 %. Je však třeba přiznat, že k hodnocení přesnosti astronomové využili přesné údaje získané radarovými metodami.

Zatímco na loňský přechod Venuše se muselo čekat 122 let, další nastane již r. 2012. Nejlépe pozorovatelný však bude v Jižní Americe.

Podrobné informace o pozorováních přechodu Venuše v r. 2004 i materiály k astronomickým tématům spojeným s přechodem mohou zájemci nalézt na www.eso.org, www.vt-2004.org, www-astronomy.mps.ohio-state.edu/~pogge/Ast... popř. http://www. transitofvenus.org/sitemap.htm.