Ještě jednou o zamrzání horké vody

Loni v listopadu se na stránkách Vesmíru diskutovalo o tom, zda je možné, že teplejší voda zmrzne rychleji než voda studená. Na poměrně jednoduchých úvahách je možno ukázat, že tento jev neplatí obecně, ale pouze za určitých podmínek.

Již staří Řekové

Ve své první knize Meteorologie (zhruba 350 let před Kristem) popisuje Aristoteles poněkud zvláštní rituál obyvatel Pontu (dnešní části severního Turecka): „Při zimním rybolovu nejdříve rozlili větší množství horké vody kolem děr vysekaných do zamrzlé řeky či jezera, a pak v rychle vznikajícím ledovém valu upevnili své rákosové udice.“ Zdá se, že Aristoteles byl jedním z prvních, kdo považoval fakt, že teplejší voda zmrzne rychleji než studená, za celkem přirozený.

Pak uplynulo více než osmnáct století, než se tímto problémem začal zabývat (v zimě roku 1461) Giovanni Marliani. V mrazivý den vzal po čtyřech uncích vařící a studené vody, a ejhle – vařící voda zmrzla dříve! Téměř o dvě stě let po něm René Descartes v „Meteorech“ (jednom ze tří dodatků „Rozpravy o metodě“) jeho názor pouze potvrdil: „Ze zkušenosti víme, že zahřátá voda zmrzne rychleji než nezahřátá.“ ¹⁾

Zájem o tento zvláštní jev se pak opět vytratil ze scény, a objevil se až koncem šedesátých let minulého století – v Africe. Mohl za to tanzanský školák Erasto Mpemba, který si při časté výrobě zmrzliny ve školní kuchyňce všiml, že výchozí směs (jejíž nedílnou součástí bylo horké převařené mléko) „zezmrzlinovatí“ rychleji, jestliže se dá do mrazáku ihned, bez předchozího chlazení na vzduchu. Mlsnost, netrpělivost a zvídavost zajistily malému Erastovi nesmrtelnost, tedy alespoň v tom smyslu, že po něm byl jev rychlejšího zmrznutí teplejší vody pojmenován. Zmrzne ale teplejší voda skutečně rychleji než studená?

Pro a proti

Od konce šedesátých let byla k tomuto problému vyslovena řada spekulací a provedena spousta experimentů. Vznikly dva názorově protichůdné tábory.

První popírá, že by vůbec Mpembův jev byl možný, a používá argumenty, které se na první pohled zdají být nevyvratitelné. Předpokládejme, že studenější vodu budeme ochlazovat (např. z počáteční teploty T_p = 20 °C), dokud úplně nezmrzne; nechť to trvá t₁ sekund. Pokud chceme, aby zmrzla i voda např. 80 °C teplá, musíme nejdříve snížit její teplotu na 20 °C za čas t₂ sekund (při téže rychlosti chlazení), čímž jsme problém převedli na předcházející případ. Další proces ochlazování (až do úplného zmrznutí) pak trvá z časového hlediska stejně dlouho (tj. t₁ sekund). Teplejší voda tedy nemůže zmrznout dříve než studená, protože t₁ + t₂ > t₁. A šmytec.

Opoziční tábor používá sofistikovanější apologetiku existence Mpembova jevu, založenou na analýze vlivu všech možných procesů, které při ochlazování a mrznutí vody mohou probíhat. Shrňme stručně jejich argumenty:

• Vypařování. Při ochlazování se voda zároveň odpařuje z volného povrchu (tam, kde je v přímém kontaktu s okolím). Jestliže byla původně teplejší, vypařuje se intenzivněji a vlastně jí už začne mrznout menší množství. Poněvadž doba tuhnutí je úměrná množství vody, lze dřívější mrznutí teplejší vody snadno vysvětlit. Má to však jeden háček: teplejší voda někdy zmrzne rychleji i v uzavřené nádobě, z níž se nemůže vypařit.
• Proudění (konvekce). Tento argument je velmi vděčný, protože exaktně se poměrně obtížně dokazuje i vyvrací. Idea je vcelku prostá ²⁾ – v průběhu ochlazování může ve vodě, popř. na jejím povrchu vzniknout proudění. Příčina může být dvojí: závislost hustoty vody na teplotě (vztlaková konvekce), nebo změna povrchového napětí vody závisející na teplotě (Marangoniho proudění). Přitom platí, že čím vyšší je počáteční teplota vody, tím vydatnější může být proudění. Těmito makroskopickými pohyby se voda promíchává a teplo z jejího objemu se přenáší ke stěnám nádoby. Může se pak stát, že jsou hranice systému teplejší než teplota uvnitř objemu, a tím se odvod tepla zrychlí. Fundamentalisté dokonce tvrdí, že právě z těchto příčin musí být křivka ochlazování teplejší vody v celém intervalu teplot strmější než křivka vody studené. I tento argument je ale nutno zařadit mezi domněnky, poněvadž konkrétní důkaz chybí.
• Změna složení. Ve vodě je obvykle rozpuštěno určité množství okolního vzduchu. Jestliže systém zahřejeme na vyšší teplotu, rozpuštěné plyny začnou unikat do okolí. V teplejší vodě je tedy mnohem méně vzduchu než ve studené. Podle obhájců Mpembova jevu může taková změna složení vody posunout její bod tuhnutí, nebo přinejmenším ovlivnit její vlastnosti z hlediska vedení tepla. (Proč „ve prospěch“ teplejší vody, to nikdo neví.) Na druhé straně bylo provedeno několik experimentů, kdy se koncentrace rozpuštěných plynů měnila záměrně, ale na Mpembův jev to nemělo podstatný vliv. Navíc i tato spekulace selhává, jestliže jde o uzavřené systémy, z nichž plyny nemohou unikat.
• Změna vlastností okolí. Z tepelného hlediska ovlivňuje teplá voda své bezprostřední okolí více než studená. Jestliže je nádoba umístěna například na ojíněný podklad, který je (špatným) vodičem tepla, může podklad (částečně) roztát, a teplo je pak odváděno rychleji. Někdy ale teplejší voda zmrzne rychleji než studená, přestože jsou nádoby postaveny na polystyrénové podložky, které teplo nevedou vůbec.

Zdá se, že argumenty pro i proti jsou na první pohled stejně silné. Ovšem podle klasické logiky nemohou mít pravdu obě strany. Nebo mohou?

K dispozici je poměrně velký počet experimentálních dat i teoretických hypotéz, s jejichž pomocí lze (na první pohled) existenci Mpembova jevu stejně věrohodně dokázat i vyvrátit. Jak z této šlamastyky ven? V podstatě je možno postupovat dvojím způsobem: Buď tento problém fyzikálně co nejpřesněji formulovat, a pak řešit systém rovnic popisujících procesy chladnutí, vedení tepla, proudění a zamrzání vody. Nebo řešení problému zjednodušit v duchu Einsteinova výroku, že vysvětlení nějakého jevu má být tak jednoduché, jak jen možno, ale ne jednodušší. Vydejme se touto cestou (viz text v rámečku) a pokusme se zjistit, za jakých okolností Mpembův jev platí a kdy vůbec mrzne voda. Při hledání odpovědi narazíme na nečekané souvislosti.

Není voda jako voda

Jestliže se zeptáme dítěte školou povinného, při jaké teplotě mrzne voda, zpravidla pohotově odpoví, že při 0 °C. Odpověď je to jednoduchá, jednoznačná, ale nesprávná. Ve skutečnosti jsou při této teplotě (za normálních podmínek) voda a led ve vzájemné termodynamické rovnováze, existují současně, ale jinak se nic makroskopicky neděje. Chceme-li, aby voda začala zamrzat, musíme snížit její teplotu pod 0 °C, tj. musíme ji přechladit. Ani to ale ještě nemusí stačit; speciální experimenty svědčí o tom, že s teplotou je možno jít dokonce až na –70 °C, aniž se objeví viditelné krystalky ledu. Co brání tomu, aby voda zmrzla?

Z teorie nukleace ³⁾ plyne, že změna skupenství vody je podmíněna vznikem mikroskopických zárodků ledu („klastrů“) v důsledku dostatečně velkých fluktuací. K tomu je nutno vynaložit určitou energii, kterou je pak možno chápat jako bariéru přechodu bránící vodě zmrznout hned po dosažení teploty 0 °C. Velikost podchlazení fyzikálně souvisí s mírou metastability původní fáze. Co je ale příčinou podchladitelnosti vody?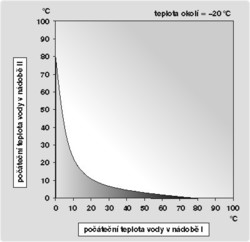

Pro odpověď musíme zajít do období zhruba 347–360 let před Kristem, kdy Aristokles, zvaný též Platon, sepsal svoje kosmologické a pythagorejsky laděné dílo „Timaios“. V tomto dialogu (či spíše dlouhém Timaiově monologu) je definováno mimo jiné pět platonských těles, s jejichž pomocí demiurg složil všehomír (a Euklides ve svých „Základech“ dokázal, že pouze tato tělesa jsou pravidelné mnohostěny). Pro nás budiž důležitým faktem to, že vodě byl přiřazen dvacetistěn – ikosaedr, tedy objekt, jehož symetrie je zcela neslučitelná se symetrií ledu krystalujícího v šesterečné soustavě, což bylo (kupodivu až v roce 2001) ověřeno difrakcí rentgenového záření. ⁴⁾ Skutečnou příčinou podchladitelnosti vody jsou tedy její strukturní vlastnosti – ke stavbě ledu máme prostě k dispozici nevhodné „cihličky“. Jestliže se má led začít tvořit i za vyšších teplot, je nutno tyto nevhodné stavební bloky rozbít – nejlépe tím, že vodu prostě zahřejeme. Čím vyšší je pak počáteční teplota vody, tím menší je koncentrace ikosaedrálních útvarů – a tím vyšší je teplota, při které začne voda zamrzat.

Konečně konec

Z uvedených skutečností plyne, že různým počátečním teplotám vody odpovídají různé teploty počátku mrznutí, při kterých se objeví první krystalky ledu. Abychom mohli určit časy, kdy první i druhá voda úplně zmrzne, musíme znát kvantitativní závislost teploty mrznutí na počátečním přehřátí. To lze buď zjistit experimentálně (např. jednoduchou sadou měření v rámci fyzikálních praktik), nebo odhadnout – křivku závislosti si můžeme nějakým způsobem „namodelovat“. Přidržme se druhé možnosti a prostě si tuto závislost vymysleme. Jen musíme mít na paměti, že jednak jde o poměrně rychle klesající funkci, jednak patrně konečný výsledek nebude v úplné shodě s naměřenými daty. Pro demonstrační účely tohoto článku to ale stačí.

A to je také přesně ta informace, která chyběla v naší skládačce. Její předností je i to, že podmínku, aby teplejší voda mrzla jako první (t_I + q_I < t_II + q_II), lze pak vyjádřit pouze pomocí kontrolovatelných veličin (počáteční teploty a stálé teploty prostředí v mrazáku). Prostor počátečních teplot teplejší i chladnější vody se pak skládá ze dvou oblastí, které určují takové kombinace počátečních teplot, při kterých zmrzne jako první ta či ona voda (viz obr.). Vždycky se ale dají najít takové kombinace počátečních teplot, pro které zmrzne teplejší voda dříve. Z rozboru zmiňované podmínky také plyne, že pravděpodobnost uskutečnění Mpembova jevu se zvětšuje, jestliže se teplota mrznutí studenější vody přibližuje teplotě okolí.

Dá se tedy říci, že teplejší voda je „jiná“ než studená, začíná mrznout při vyšší teplotě a může někdy zamrznout i dříve než studená. Jedna z hlavních příčin tkví v její „geometrii“: základní strukturní prvky vody (tzv. uspořádání na krátkou vzdálenost) vykazují ikosaedrální rysy.

Odkud to ale, k čertu, mohl vědět Platonův Timaios?