Zákeřné dopravní zácpy
Cestovat autem bývá občas psychicky náročné. Každý ví, že ani po dálnici se nejede rovnoměrně přímočaře jako v učebnici fyziky. I na dálnici do cesty přicházejí nerovnosti vozovky, náhlý boční vítr či zatoulané kočky a to řidiče nutí stále měnit rychlost jízdy. Občas se dokonce na silnici pracuje a všechna vozidla se musí vtěsnat do jednoho pruhu, což je výrazně zpomalí, jako když voda z láhve musí vytékat dosti úzkým hrdlem.
Jsme-li na dálnici sami, je toto vše sice nepříjemné, ale pořád to ještě není taková pohroma, jaká nás potká při dopravní zácpě. K tomu musí být aspoň dva: zácpa vznikne tehdy, když musíme brzdit či zastavit ne proto, že bychom potkali objektivní překážku, ale že nás zdržuje auto před námi. Nemusíme přitom vůbec vědět, proč auto před námi zpomalilo, zda má před sebou objektivní překážku nebo opět jen jiné auto, které je zdržuje. Zácpa má sice na počátku nějakou příčinu v situaci na vozovce, pak se ale osamostatní a udržuje se sama sebou. Výsledný obraz je takový, že „se tam vpředu cosi stalo“, že nějaká nicotná příčina způsobila řetězovou reakci brzdění, která se, je-li provoz dost hustý, protáhne libovolně daleko. Na dálnici se budou vyskytovat zácpičky, zácpy i úplné kolapsy. Přitom není nadsázkou říkat, že „lidi si to dělaj sami“: zácpy vznikají teprve tehdy, když je mnoho lidí pohromadě. Dopravní zácpy jsou kolektivní jev. 
Podívejme se pozorněji na to, co se při takové zácpě děje. Obr. obrázek ukazuje data získaná leteckým fotografováním na dálnici v Německu. Vodorovně je vynášena prostorová souřadnice podél dálnice, svisle dolů plyne čas. Každá čára představuje jeden automobil. Nahuštěniny čar, to jsou právě dopravní zácpy. Vidíme především, že taková zácpa dovede přežívat značně dlouho, aniž by však setrvávala na tomtéž místě. Pohybuje se jako celek stálou rychlostí proti směru pohybu jednotlivých aut a udržuje si svou identitu. Dopravní zácpa má jakoby svou vlastní individualitu. Je to objekt, který povstává emergentně, jako výsledek složité kolektivní interakce individuí – aut. Dopravní systém se spontánně organizuje do soustavy dopravních zácp.
Modelujeme rádi, protože si připadáme jako malí stvořitelé, a dělá nám radost, když vymodelujeme něco, co se trochu podobá dílu toho velkého Stvořitele. Máme pocit, že jsme mu trochu nakoukli pod pokličku a prokoukli jeho fintu, „jak se to dělá“. Leccos se nám modelovat daří, třeba vítr v aerodynamických tunelech, a těmito úspěchy povzbuzeni, pouštíme se stejným způsobem i do sociálních jevů, jako jsou například dopravní zácpy.Představme si silnici jako úsečku a na ní rovnoměrně rozmístěné body. Auta se mohou nacházet v těchto bodech. Experimentátoři zjistili, že na jedno auto je třeba počítat asi se 7,5 metru, to bude tedy vzdálenost, která v realitě odpovídá vzdálenosti mezi dvěma sousedními body. Automobily budou moci mít rychlost v = 0,1,2,...vmax. Jak běží čas, pohybují se jednak podél úsečky a zároveň se také mění jejich rychlosti, jako reakce na dopravní situaci. Pravidla zrychlování a zpomalování mohou být dosti složitá, ale my si je zjednodušíme takto:
K tomu připočtěme ještě pravidlo o pohybu:
Zatímco poslední pravidlo o změně polohy je evidentní a je dáno prostým principem dráha = rychlost × čas, pravidla o zrychlování jsou dána psychologií řidiče a jsou sama o sobě komplexní. Nejenže je zde veliká rozmanitost možných reakcí podle konkrétní situace, ale i každý z řidičů reaguje jinak. Abychom se v tom aspoň trochu vyznali, opomiňme komplexitu vnesenou složitými lidskými reakcemi a soustřeďme se jen na tu komplexitu, která zůstává i tehdy, když se řidiči chovají jako jednoduší roboti podle prvních tří pravidel.
Nejprostší otázkou, kterou můžeme modelu položit, je,
která se na ní nacházejí. Ukazuje se, že existuje kritická hustota, která dává maximální propustnost. V měřeních reálného provozu se zjišťuje hodnota kolem 0,18, tedy v úseku 7,5 metru vymezeném pro jedno vozidlo se v případě největší propustnosti bude nacházet v průměru 0,18 automobilu. Závislost má zvláštní tvar: pro malé hustoty téměř lineárně stoupá k maximu, pak se zalomí a opět téměř lineárně klesá. Stejné chování bylo pozorováno v simulacích. Na obrázcíchPro celkový dojem je nejlepší sledovat pohyb každého jednotlivého auta v časoprostorovém obrázku podobném tomu, který máme z leteckých pozorování skutečného provozu. Nejjednodušší situace nastává, pokud rychlost může být pouze 0 nebo 1. Auta v zácpě mají rychlost 0, všechna ostatní maximální rychlost 1. Náhodné zpomalování vede ke vzniku emergentních zácp, které se pohybují konstantní rychlostí proti směru pohybu jednotlivých aut. Zácpy přitom mohou narůstat či se zmenšovat, jak auta vpředu zácpu opouštějí a vzadu ji jiná auta doplňují. Záleží pak na hustotě aut, zda vzniklá zácpa bude mít spíše tendenci mizet (ubývá-li vpředu více), nebo narůstat k úplnému kolapsu (přibývá-li více zezadu). Jak se bude zácpa přesně vyvíjet, to nevíme: Auta před ní a za ní jsou rozmístěna s určitou průměrnou hustotou, ale kde se přesně nacházejí, o tom nemáme informaci. Známe tedy jen pravděpodobnosti, že se zácpa prodlouží o jedno vozidlo a že se o jedno vozidlo zkrátí.
Ukazuje se, že musíme rozlišit tři režimy. Podkritický režim při malé hustotě provozu, to je ten, kdy pravděpodobnost přirůstání zácpy zezadu je menší než pravděpodobnost odpoutávání vozidel vpředu. Zácpa může vzniknout, ale protože má tendenci mizet, nikdy netrvá příliš dlouho. Celkový obrázek je takový, že na pozadí plynulého provozu se tu a tam objeví zácpy omezené velikosti. Průměrná velikost zácpy se sice bude zvětšovat, bude-li přibývat aut, ale stále zůstane omezená. Naproti tomu při nadkritickém režimu, když hustota vozidel je velká, je větší pravděpodobnost toho, že zácpa, jakmile jednou vznikla, vzrůstá. Je jasné, co nastane: Silnice je plná zácp a máte spíš štěstí, když zrovna v žádné nejste. Pro pozorovatele z letadla je na pozadí jedné veliké zácpy něco málo míst, kde se auta pohybují. Tyto „díry“ se zmenšují, když hustota aut vzrůstá.
Pokud si budeme představovat auta jako molekuly jakési kapaliny, můžeme se na podkritický provoz dívat jako na obyčejné laminární proudění tekutiny v trubici, proudění nebrzděné žádnými víry. Nadkritický provoz pak bude odpovídat proudění s rozvinutou turbulencí, kde se ve vírech ztrácí téměř všechna energie, kterou tekutině dodáváme (například v silně zarezlém potrubí, jak dobře vědí obyvatelé horních pater starých činžovních domů).
Nejzajímavější je to ovšem právě na hraně mezi těmito dvěma režimy, neboli v kritickém stavu. Je to právě ten stav, kdy křivka průjezdnosti (obr.
Kritický stav je přitom důležitý tím, že je to právě stav s maximální průjezdností: podkritický stav není optimální, jelikož dokáže pojmout ještě další auta. Nadkritický stav není optimální, protože typickou situací je obrovská zácpa a pohyb je omezen jen na „díry“. Vrátíme-li se k analogii s fázovým přechodem u tekutin, maximum průjezdnosti v kritickém bodě dopravy může zhruba odpovídat maximu měrného tepla v bodě fázového přechodu.
Zatím jsme si situaci zjednodušovali tím, že jsme rozdělovali vozidla jen na stojící a jedoucí, neboli rychlost byla 0 nebo 1. O něco realističtější bude, když roztřídíme auta do, řekněme, šesti rychlostních kategorií, tedy v = 0, 1, 2, 3, 4, 5. Co se děje, můžeme pozorovat na obr. obrázek. Opět, jako dříve, vidíme zácpy jako samostatné objekty, pohybující se proti směru aut, vznikající, přežívající určitou dobu a opět mizející. Co je zde nové, je větvení zácp: už nejde o kompaktní objekty, které se vyvíjejí pouze přirůstáním zezadu a „vypařováním“ vpředu, ale automobil, který právě opustil přední okraj zácpy, může být vzápětí zase zpomalen, ještě než získá maximální rychlost (je-li maximální rychlost 5, může jí dosáhnout nejdříve za 5 časových jednotek). Tím ovšem generuje novou zácpu v těsné blízkosti zácpy původní. Dá se to také popsat tak, že zácpy se nevyskytují nezávisle na sobě, ale spíše v jakýchsi shlucích, vzniklých rozštěpením jedné původní zácpy. Z pohledu řidiče to znamená, že jakmile se dostane do jedné zácpy, je dosti pravděpodobné, že se po jejím opuštění brzy dostane do jiné.
Dosud jsme pozorovali situaci jaksi z ptačí perspektivy, z pohledu hlídky ve vrtulníku přelétávajícím nad dálnicí. Když se posadíme za volant a projíždíme zácpami s řidičem, pohled se nám doplní o další poznatky. O tom, jak závisí průjezdnost dálnice na hustotě aut, jsme už mluvili. Když řidič plánuje svou cestu, zajímá ho také, do jaké míry se může spolehnout, že očekávaná doba jízdy bude odpovídat skutečnosti, neboli jaké jsou průměrné odchylky od průměrné doby jízdy. Zatímco pro dopravního dispečera je dobrou zprávou, když se průjezdnost blíží k maximu, řidič není potěšen, když je nejistota týkající se délky jízdy příliš velká. Ukázalo se však, že maximální průjezdnost i maximální neurčitost doby jízdy nastávají právě v kritickém stavu. Tedy technikové, snažící se protlačit komunikacemi co nejvíce aut, táhnou dopravu ke kritické situaci, v níž je sice největší průjezdnost, ale řidič vůbec neví, jak dlouho mu bude skutečně cesta trvat. Jelikož v kritickém stavu máme zácpy všech velikostí, může se stát, že projedeme silnici jen s maličkým zdržením, ale také se může stát, že náhodou narazíme na obrovskou zácpu, trvající mnoho hodin... Nebylo by tedy moudřejší být skromný a nechat provoz v nikoli optimálním, zato však předvídatelnějším stavu? Můžeme na to namítnout třeba to, že celý život je velmi nepředvídatelný, jak konečně zdůrazňují ti, kteří tvrdí, že život se odehrává na „hraně chaosu“, v kritickém bodě mezi banální jednoduchostí a nezvládnutelným zmatkem (viz též článek Jiřího Doskočila „Život na ostří nože“, Vesmír 74, 324, 1995/6). Za maximální efektivitu platíme maximálním stresem.
Zdá se tedy, že chování dopravního systému je řízeno právě počtem aut na jednotku délky silnice. To by však bylo pravda jen za předpokladu, že hustota vozidel nezávisí na provozu. Mohlo by to například nastat, kdyby auta jezdila stále dokola uzavřeným městským okruhem. Nic do něj nepřijíždí, nic neodjíždí, průměrná hustota aut tedy opravdu zůstává konstantní. Zda takový obrázek odpovídá skutečnosti, není jistě nutno dlouze rozebírat. Reálný dopravní systém se vyznačuje právě otevřeností. Dálnice je spíše něco jako trubice (plná nerovností, záhybů atd.) otevřená na obou koncích. Na jednom konci čeká zásobárna aut, na druhém konci auta vytékají ven.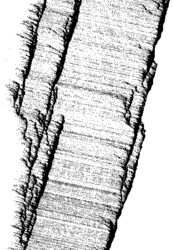 
Kolik aut se skutečně nachází na dálnici, závisí nikoli na nás, kolik jsme jich tam zvenčí umístili, ale na okamžité dopravní situaci. Každá zácpa poněkud hustotu aut sníží (neboť vstupem jich nemůže tolik přibývat) a když zmizí, hustota má šanci opět vzrůst. Hustota zácp a hustota vozidel působí proti sobě. Vyšší hustota aut způsobí více zácp, což opět hustotu aut sníží a tím se průměrný počet aut na dálnici udržuje samoregulací na určité stálé hodnotě. (To vše ale za předpokladu, že na vstupu je stále připraveno dost vozidel, jako například v pátek večer, kdy všichni najednou opouštějí své město, aby se přesunuli jinam.) Nejdůležitějším zjištěním na tom všem je to, že tato samoregulovaná hustota je právě rovna kritické hustotě. Dopravní systém se tedy sám, i bez zásahu různých dispečinků, nastaví do stavu s největší propustností – a také s největší neurčitostí, co se týče skutečné doby jízdy.
To, co tu popisujeme, je příkladem mnohem obecnějšího jevu, který se nazývá samoorganizované kritično (self-organized criticality: viz též Vesmír 76, 283, 1997/5). Kritický stav nenastavil nikdo zvnějšku, příroda si ho vybírá sama. 
Zácpy a nepředvídatelně dlouhé čekání v nich nejsou tedy způsobeny nějakými nedokonalostmi, neschopností či zlou vůlí, ale je to přirozená situace, k níž každá dopravní síť směřuje. Pokud se nám takový stav nelíbí, máme řadu možností, jak na něj reagovat. V každém případě však nám bude užitečné vědět, k čemu tíhne náš protivník sám od sebe, abychom se pak rozhodli, jak na to odpovíme my.
Literatura
Per Bak : How nature works – the science of self-organized criticality, Springer 1996K. Nagel and M. Paczuski : Emergent traffic jams, Phys. Rev. E 51 (1995) 2909
STATISTICKÁ FYZIKA, NÁHODNÁ PROCHÁZKA A DOPRAVNÍ ZÁCPA
Statistická fyzika se dokáže na zácpy dívat jako na problém náhodného chodce. Představme si, že počet aut v určité zácpě nám ukazuje statista kráčející podél nataženého provazu s uzly: jeden uzel je jeden krok. U kolikátého uzlu od začátku provazu se statista právě nachází, tolik je v zácpě aut. Je-li na samém začátku, zácpa tu není. S pravděpodobností p vzniká zácpa v důsledku náhodného vnějšího vlivu. Pro našeho statistu to znamená, že vyrazí od začátku provazu a udělá krok vpřed. Nyní mu nastává drama: zezadu přibude auto s pravděpodobností p1, vpředu jedno ubude s pravděpodobností 1-p. Statista má tedy tři možnosti: krok zpět (pravděpodobnost (1-p1)(1-p)), krok vpřed (pravděpodobnost p1p), anebo zůstat na místě (pravděpodobnost p1(1-p)+(1-p1)p). Jeho pohyb podél provazu tedy připomíná náhodnou procházku po polopřímce. Jak dlouho trvá zácpa, to je doba, která uplyne od okamžiku, kdy statista vykročil od počátku provazu, až do chvíle, kdy se do počátku opět vrátí? V teorii náhodných procházek je problém výpočtu této doby dobře znám a řešen, takže výsledky můžeme přenést přímo zpět na naše dopravní zácpy.
Rozlišujeme zde tři režimy. PODKRITICKÝ REžIM, to je ten, kdy náhodný chodec má větší pravděpodobnost se vracet než kráčet kupředu ((1-p1)(1-p)> p1p). Zácpa má tendenci mizet. Průměrná velikost zácpy je omezená. Naproti tomu při NADKRITICKÉM REžIMU je větší pravděpodobnost toho, že zácpa, jakmile jednou vznikla, vzrůstá, neboli statista spíše kráčí kupředu. Typická zácpa je nekonečně veliká a konečné jsou naopak „díry“ mezi zácpami. KRITICKÝ BOD odpovídá rozhraní mezi těmito dvěma režimy.
Vypočteme-li průměrnou velikost zácp a „děr“ v kritickém bodě, dostaneme v obou případech nekonečno. Kritický bod tak představuje bod fázového přechodu mezi „plynným“ stavem s malou hustotou aut a konečnými zácpami, a „kondenzovaným“ stavem s vysokou hustotou aut a konečnými „dírami“.
V kritickém stavu má náhodný chodec stejnou pravděpodobnost, že půjde vpřed jako že půjde vzad, může se zatoulat dosti daleko a pak se stejně vrátit zpět. V tomto případě jde o klasickou náhodnou procházku, jak se o ní mluví v teorii pravděpodobnosti. Ta nám také hned řekne, jaká je pravděpodobnost procházky trvající t časových jednotek, neboli pravděpodobnost, že dopravní zácpa bude mít trvání t. Je to P(t) ~ t–3/2. Podstatné na tomto výsledku je především to, že jde o mocninnou závislost, konkrétně mocninu s exponentem –3/2. Tento typ závislosti je dobře znám z fyziky, z teorie fázových přechodů: v kritickém bodě je pravděpodobnost, že odchylka od průměru bude mít rozsah t, úměrná nějaké mocnině t, neboli P(t) ~ t–α . Zácpu si můžeme představit jako odchylku od normálu, jímž je nerušený provoz, a za míru této odchylky brát trvání zácpy.
Mocninná závislost pravděpodobnosti takové odchylky se vyskytuje právě jen v kritickém bodě a má magickou vlastnost zvanou invariance škál. Vysvětlíme si to takto: Představme si, že měříme čas hodinkami, které tiknou jednou za 1 sekundu. Srovnávejme pravděpodobnost zácpy trvající 1 tiknutí (1 sekundu) s pravděpodobností jiné, trvající 10 tiků. Bude 1–3/2 /10–3/2 = 31,62...krát pravděpodobnější, že zácpa bude trvat 1 tik, než že bude trvat 10 tiků. Nyní si představme, že ve spánku z nás nějaký čaroděj udělal lenochoda, jehož hodinky tikají ne jednou za sekundu, ale jednou za celý den, to je 86 400 sekund. Srovnávejme opět pravděpodobnost zácpy trvající 1 tik se zácpou trvající 10 tiků. Vyjde, že jednotiková bude (1×84400)–3/2/(10×84400)–3/2 = 31,62... krát pravděpodobnější než desetitiková. Totéž co předtím! Zácpy nám neřeknou, jak rychle jdou naše hodinky, neboli jakou časovou škálu používáme. Nemáme-li jiný prostředek (u dálnice třeba nejsou žádné veřejné hodiny, slunce a měsíc zmizely...), nemůžeme to nijak zjistit. V kritickém stavu jsou si časové škály navzájem rovnocenné.
SAMOORGANIZOVANÉ KRITIČNO
Poprvé tento jev systematicky studovala r. 1987 trojice P. Bak, Ch. Tang a K. Wiesenfeld na zjednodušených modelech „pískových kup“. Později se sice zjistilo, že skutečné kupy písku se podle jejich modelů nechovají, nicméně se našla řada dalších aplikací, které vysvětlují mnohá pozorování. Například seizmologové znají Guttenbergův-Richterův zákon, který říká, jaká je průměrná četnost jak velkých zemětřesení. Plyne z něj, že zemská kůra se neustále nachází v kritickém stavu. Tento zákon lze vysvětlit pomocí poměrně jednoduchého modelu, který vykazuje samoorganizované kritické chování.
Dynamiku samoorganizovaného kritického systému lze popsat jako soupeření dvou procesů:
1) velmi pomalé, „geologické“, pochody pozvolna zvyšují v systému „pnutí“, například tím, že se po sobě posouvají kontinentální desky,
2) v nejnamáhanějším bodě to praskne a porucha se lavinovitě šíří velkou rychlostí dál. Napětí se uvolnilo, ale pomalé pochody ho po čase opět zvýší. Celkové pnutí tak stále kolísá kolem kritické hodnoty. Sledujeme-li četnost lavin v závislosti na jejich velikosti, dostaneme mocninný zákon: neklamný signál kritického stavu.
Takto se vysvětlují nejen zemětřesení a dopravní zácpy, ale i vymírání druhů (vymření jednoho druhu bakterie vede k vymření několika druhů hmyzu, to pak k vymření žab, to pak k vymření dinosaurů...), burzovní krachy, záplavy na Nilu a spousta dalších zajímavých jevů. V teorii samoorganizovaného kritična se daří vtěsnat takové jevy do společného rámce, položíme-li tato rovnítka: lavina = dopravní zácpa = zemětřesení = hromadné vymírání druhů = hospodářská krize = záplava = atd. atd.
Ke stažení
Článek ve formátu PDF [411,72 kB]
O autorovi
František Slanina
Doporučujeme
Se štírem na štíru
Ustrašená společnost 
