Pocta Descartovi
RENATUS DES-CARTES, DOMINUS DE PERRON, NATUS HAGAE TVRONVM, ANNO, M.D.XCVI, VLTIMO DIE MARTII
 31. března letošního roku jsme v tichosti vzpomněli čtyřstého výročí narození René Descarta. V září se bude sice ještě konat krátká konference o Descartovi zvláště se zřetelem ke vztahům s Komenským, ale to bude vše. To před sto lety byly oslavy třístého výročí narození Descarta okázalejší. Slavnost byla konána dne 6. prosince o 10. hodině dopolední:
31. března letošního roku jsme v tichosti vzpomněli čtyřstého výročí narození René Descarta. V září se bude sice ještě konat krátká konference o Descartovi zvláště se zřetelem ke vztahům s Komenským, ale to bude vše. To před sto lety byly oslavy třístého výročí narození Descarta okázalejší. Slavnost byla konána dne 6. prosince o 10. hodině dopolední:
Zasedací síň radnice pražské byla ochotou obce vykrášlena palmami a jinými rostlinami ze skleníků městských a uprostřed zeleni v průčelí sálu skvěla se podobizna oslavencova. Smíšený komitét pro přípravy oslav Descartových, složený z členů Jednoty mathematické a Spolku filosofického se schválením a na účet Jednoty mathematické opatřil olejový obraz oslavence od akademického malíře p. Josefa Ženíška (obraz dodnes opatruje Jednota českých matematiků a fyziků, s jejímž laskavým svolením jej zde reprodukujeme).
Velká síň záhy před 10. hodinou naplnila se vzácným a vybraným obecenstvem. Byly tu zastoupeny: Česká akademie věd císaře Františka Josefa, Učená společnost, vysoké školy universitní i technické a střední školy pražské, zástupcové české žurnalistiky, spolky národní a vědecké a jiné korporace; zvláště byli přítomni: dvorní rada prof. dr. Randa, rektor české techniky, prof. Fr. Müller, děkan filosofické fakulty, prof. dr. Král, první náměstek starosty obce Pražské (nynější starosta) dr. Podlipný, členové městské rady, za jednotu pošumavskou předseda dr. Edvard Baštýř, za jednotu severočeskou místopředseda prof. dr. Pastrnek, za výkonný výbor národní strany svobodomyslné inženýr O. Materna, za spolek českých lékařů předseda dr. Prokeš, za spolek českých mediků MUC. Vinař, za klub přírodovědný starosta prof. Wurm, za redakci ‘Vesmíru’ prof. Nekut, za Alliance française prof. Pinkas, báňský hejtman A. Pallusch, vrchní ředitel zemské banky dr. Mattuš, polní podmaršálek svob. p. z Friedbergů, zemský inspektor školní dr. Hejzlar, místopředseda banky Slavie, docent a ředitel K. P. Kheil, theol. dr. Sýkora, ředitel českoslovanské akademie obchodní Tonner, prof. dr. Lambl, setník P. Blažek, výbor Jednoty mathematiků českých, výbor spolku českých filosofů s předsedou prof. dr. Drtinou, ředitelé středních škol. Mimo to shromáždilo se velké množství posluchačstva vysokých škol a četné dámy. Hlavními řečníky byli prof. Studnička a prof. Durdík. Krátce po 10. hodině vystoupil na řečniště předseda Jednoty mathematické gymn. řiditel M. Pokorný a měl tuto řeč úvodní:
Slavné shromáždění! Velectěné dámy a velectění pánové!
Letos jest tomu tři sta let, co ve Francii v městě Lahaye spatřil světlo světa René Descartes, seigneur du Perron, známý také zlatinisovaným jménem: Renatus Cartesius. Jakkoli historie střízlivým a objektivním zrakem svým hledí zpět do minulosti člověčenstva a přesnou váhou svého soudu odměřuje zásluhy ať národů ať jednotlivců naprosto spravedlivě, ceníc je tím výše, čím hlouběji a trvaleji působily na prospěch a pokrok lidstva, přece v povšechné paměti potomstva nejsou pro všechny zásluhy předků stín a světlo rozděleny stejnou měrou. Kdo ze vzdělanců neznal by činy veliké, pojící se ke jménům Alexandra Makedonského, Caesara, Attily, Čingischána, Napoleona atd., jejichž dráha činnosti označena byla šlépějemi naplněním krví a spoustou? Velcí ti dobyvatelé, ti budovatelé i ničitelé říší zajisté slaví se v paměti vzdělaného světa mnohem výše, než velikáni z říše myšlenkové, pro jejichž činnost nezřídka i na rtech vzdělance vyskytá se pouze úsměšná poznámka o ‘neplodné spekulaci’. Nemůžeme ovšem vinu takového pojímání zásluh přičítati společnosti vzdělanců, nýbrž zajisté jen pramenům, z nichž své vzdělání, tak zvané ‘povšechné’ čerpali. Prodromus vzdělanosti naší obecné není nikterak zřízen tak, aby ji skutečně poskytoval a co v něm především schází téměř úplně, to právě jest sama historie vzdělanosti, osvěty a pokroku, jediná to historie skutečně povšechná.
Nejde mi zde ani tak o okázalost tehdejších oslav, hojnou účast na nich, ba ani o to, že slova řiditele Pokorného zůstávají nezměněna v platnosti, nýbrž o to, že nikoho z tehdy přítomných nenapadlo, že by se měl nějaký ten spis Descartův vzdělat v jazyce českém. Výsledek je přes všechny slavnostní řeči smutný: národ český se svými dvěma brožurkami (Rozprava a Meditace) stojí ve frontě do duchovní Evropy až někde na samém konci. Někoho by mohlo napadnout: přece to překládat nemuseli, každý uměl latinsky a francouzsky. Dejme tomu. Tak proč je tedy aspoň nenapadlo nakoupit knihy Descartovy v hojnějším počtu, aby po dalších sto letech nebylo hotovým utrpením některé z nich se domoci v našich knihovnách? Ale ani to pořád není to, co by mi vadilo. Co mi opravdu vadí, je, že už to nikomu nevadí.
Můžeme si o Descartovi myslet cokoli, ignorovat ho ale nelze. Je v kořenech naší současné vědy a chceme-li si odpovědět na otázku, kde to vlastně jsme a kam jdeme, nezbude než se jako v psychoanalýze ponořit do hlubin minulosti a vytáhnout na světlo to, co tam skryto a neuvědomováno působí. Prostě, vytěsněný a sublimovaný Descartes může působit jako fantom.
Jak víme, fantomy to také začalo: navštěvovali mladíka Descarta, a dokonce ho sužovali i tělesně. Vrcholu to dosáhlo oné památné noci v den sv. Martina z 10. na 11. listopadu 1619, v jizbě v Ulmu či okolí Ulmu, kdy byl třikrát navštíven ve snu. V prvním snu byl hnán zlým duchem k chrámu. Probudil se bolestmi, ale po dvou hodinách usnul znovu. Druhý sen byl také děsivý: uslyšel hřmot a ránu blesku; to si později vyložil jako znamení ducha pravdy, který do něj vstoupil. Opět usnul a třetí sen už děsivý nebyl: na jeho stole se záhadně objevily dvě knihy: nějaký slovník a vedle něj Corpus Poetarum – ten Descartes otevřel a jeho zrak padl na počáteční slova dvou Ausoniových básní: Quod vitae sectabor iter (Jakou cestou mám jít) a Est et non (Ano a ne). Slovník představoval podle Descartova výkladu soubor věd a Corpus Poetarum pak spojení filozofie s moudrostí. Descartes byl přesvědčen, že do něj vstoupil duch pravdy a že mu pomohl otevřít bohatství všech věd, a to poznáním vědy univerzální: X Novembris 1619, cum mirabilis scientiae fudamenta reperirem. Ulm Descartes opustil ještě než se skončila zima; byl dobrovolníkem ve vojsku Maxmiliána Bavorského, který 8. prosince 1620 zvítězil na Bílé hoře. O dva dny později, 10. listopadu 1620, si Descartes poznamenal opět une invention admirable (nevíme ovšem čeho).
Univerzální věda má být založena na ‘obdivuhodné metodě’, která povede lidského ducha systematicky k objevování všech pravd. Prvně formuloval zásady této metody sám pro sebe ve spise Regulae ad directionem ingenii, ‘Pravidla pro řízení rozumu’ – vyšel až po Descartově smrti (1650) v roce 1701.
Když si takto formuloval pravidla metody (je jich v Regulae jedenadvacet), hodlal Descartes rozvinout svůj Projekt univerzální vědy. První jeho vydaná kniha však nese název skromnější: Discours de la méthode pour bien conduire sa raison, chercher la vérité dans les sciences – Rozprava o metodě, jak správně vésti svůj rozum a hledati pravdu ve vědách. Vyšla u Iana Maira v Leydenu r. 1637 a na titulním listě je obraz muže s rýčem v ruce, soustředěného na svou práci. Nad obrázkem je nadpis: Fac et spera – Pracuj a doufej. Descartes sám se takto stylizoval do postavy oráče, který kypří a připravuje půdu. Jinde (v dopise Mersennovi) o sobě píše jako o architektovi, který rozvrhuje plán stavby, jejíž provedení ponechává tesařům a zedníkům. Rozpravu doprovázely tři eseje (pokusy, ‘okusy’), jejichž prvořadým cílem bylo ilustrovat účinnost této metody ve třech odlišných vědách: dioptrice (vědě o lomu světla), nauce o meteorech a geometrii. Zatímco Rozprava sama je vydávána často (máme i český překlad), tyto tři eseje jsou vydávány jen zřídka, ačkoli právě ony (zvláště Geometrie) určily směr vývoje vědy na staletí kupředu.
Právě proto jsem se rozhodl, že Descartovo výročí uctíme nejlépe radostí a potěšením z četby jeho Geometrie: připravil jsem překlad, doplnil faksimile latinského vydání (jímž se především Geometrie šířila, a které kupodivu nebylo nikdy reprodukováno) a otevřel Descartovský seminář, v němž Geometrii čteme a komentujeme. Když píši tuto Poctu, jsme uprostřed práce, ale myslím si, že už jistou zprávu podat mohu.
Řecká matematika byla založena na tom, čemu bychom mohli říkat geometrická algebra. Řekové zacházeli s útvary tak obratně, jako my se symboly. Mezi základní operace patřilo utvoření obdélníku ze dvou úseček (‘násobení’) a ‘přistavení’ nějaké úsečky k úsečce dané tak, aby se výsledný obdélník rovnal čtverci nad nějakou jinou danou úsečkou (‘dělení’); odpovídající sloveso bylo parabalein, odtud parabola. Je tady ale jedno omezení, na něž Descartes upozorňuje: máme-li tři úsečky, můžeme z nich udělat krychli (‘vynásobit je’), ale co se čtyřmi, pěti atd. úsečkami – tomu nic geometricky neodpovídá. To byla podle Descarta překážka bránící tomu, aby Řekové mohli zkoumat systematicky křivky vyšších stupňů. A křivky složitější potřebovali.
Podívejme se nejprve na jednu ze základních úloh geometrické algebry: Máme nalézt čtverec, který má stejný obsah jako daný obdélník: má-li daný obdélník strany FG a GH, pak je naším úkolem nalézt úsečku EF tak, aby poměr FG k EF byl stejný, jako poměr EF k GH. Úsečce EF se pak říkalo střední úměrná mezi úsečkami FG a GH. Řešení pomocí pravítka a kružítka bylo pro Řeky hračkou. Následující obrázek je vyňat z Geometrie (Discours, 1637, str. 298):
GI je kolmá na FH a FIH je polokružnice; úhel FIH je podle Thaletovy věty pravý, a tudíž trojúhelníky FGI a IGH jsou podobné, takže FG se má k GI tak, jako GI k GH, takže GI je hledaná úsečka EF. (Varování: i profesionální matematici při četbě této a následujících pasáží používají tužku a papír – a koš na odpadky, jak se říká ve známé anekdotě.)
A jsme u základního kamene řecké matematiky: tím byly poměry a úměrnosti. Poměr (logos; toto slovo přeložil Cicero jako ratio, odtud pak také naše ‘racionalita’) mezi dvěma úsečkami nelze definovat (Eukleides říká pouze, že je to nějaký vztah). Co však definovat lze, je rovnost dvou poměrů, tj. kdy jsou dva poměry ana logos – v [témž] poměru (odtud pak naše ‘analogie’). Předcházející úloha těsně souvisí s jinou úlohou, totiž úlohou o zdvojení čtverce: ke čtverci, jehož stranou je AB, nalézt čtverec o straně CD, jehož plošný obsah bude dvojnásobkem čtverce o straně AB. Hledaná CD je střední úměrná mezi úsečkami AB a dvojnásobkem úsečky AB a může být tudíž zkonstruována pomocí pravítka a kružítka. Při řešení obdobné úlohy pro krychli (zdvojnásobení obsahu krychle) se narazilo na vážný problém. Je-li totiž strana výchozí krychle AB, je třeba nalézt dvě střední úměrné mezi úsečkami AB a dvojnásobkem AB, řekněme úsečky CD a EF, tak, aby se AB mělo ku CD stejně, jako se má CD ku EF, a opět stejně jako se má EF ku dvojnásobku AB. Pak CD je hledanou stranou dvojnásobné krychle. Jenže dvě střední úměrné se už nedají nalézt pouze pomocí pravítka a kružítka, k jejich nalezení je zapotřebí nějaké kuželosečky. A řečtí matematici našli řešení této úlohy pomocí kuželoseček a sestrojili i mechanická zařízení k nalezení těchto středních úměrných.
Předpokládám, že předcházející výklad vám způsobil určité potíže – jak totiž vidět, že CD je opravdu onou hledanou stranou? Pro Řeky to problém nebyl, ti uměli zacházet běžně s útvary a úměrnostmi. Možná jste si řekli: známou stranu dané krychle si označíme a, neznámou stranu dvojnásobné krychle x, v úměrnostech vystupuje ještě další neznámá úsečka EF a tu označíme y. Rovnice pro x a y jsou pak a/x=x/y=y/2a a z nich dostaneme x2 = ay, 2ax = y2, což jsou rovnice dvou parabol, jejichž průsečík je hledaným řešením. Dále máme x4 = a2y2 = 2a3x, takže skutečně je x3=2a3.
Jenže to, co jsme právě udělali, udělali jsme díky Descartovi. Geometrie totiž začíná slovy: “Všechny úlohy geometrie lze snadno převést na takové členy (rozumí se členy, termíny, úměrnosti), k jejichž sestrojení stačí znát pouze délky nekterých úseček.″ Abychom se v těchto úsečkách vyznali, pojmenujeme si je, píše dále Descartes, a to tak, že úsečky známé označíme malými písmeny ze začátku abecedy, tj. a, b, c, ..., a úsečky neznámé pak malými písmeny od konce abecedy, tj. z, y, x, ... Všimněte si zde obráceného pořadí označování neznámých veličin; ale ještě v průběhu Geometrie přejde Descartes na běžné pořadí x, y, z. Ano, Descartova Geometrie je tou knihou, kde se poprvé objevilo naše značení, naše známá ‘neznámá x’. Ale to není všechno. Vzápětí zavede Descartes další dnešní značení: a2 je aa, a3 je aaa atd.; vlastní značení čtverce a2 však Descartes téměř nepoužívá, neboť neshledává žádnou (typografickou) výhodu proti aa. A pořád to není ještě všechno: na straně 3 čteme: a napíši √(a2+b2) pro druhou odmocninu z a2+b2. Znak pro odmocninu √ se už používal, ale Descartovou inovací je ona vodorovná čára nad odmocňovaným výrazem. Za to, že jsme si před chvílí mohli napsat rovnici a/x = x/y, vděčíte také Descartovi. Za co? Za znak pro rovnost! Ne sice za dnešní znak ’=’, ale za vůbec nějaký; Descartes používal znak blízký znaku ∞.
 Na dalším faksimile prvního vydání vidíte poprvé ‘pořádně’ zapsanou rovnici, totiž z2=az+b2. Zůstaňme u toho chvilku. Říká se tam, že k řešení této rovnice si nakreslíme nejprve trojúhelník NLM, jehož strana LM se rovná b a strana LN je ˝a. Prodloužíme-li přeponu MN do bodu O tak, aby se ON rovnalo NL, je hledané z rovno OM. (Pokuste se to uvidět, rozumí se jen z podobností nějakých trojúhelníků.) A jestliže pak výsledek zapíšeme (s použitím Pythagorovy věty), dostaneme z=ON+NM=LN+NM=½a+√(¼a2+b2), což je z gymnázia známý vzoreček pro řešení kvadratické rovnice. Chybí tam ono ±, ale záporné kořeny Descarta nezajímají (říká jim ‘nepravé’ a samozřejmě s nimi umí také zacházet), protože jim nemůže odpovídat nějaká délka úsečky. Všechny veličiny (zde a, b) se rozumějí kladné (nebo nulové). Všiměte si také sazečových rozpaků nad dosud nevídanými exponenty; vysázel je prostě do samostatného řádku.
Na dalším faksimile prvního vydání vidíte poprvé ‘pořádně’ zapsanou rovnici, totiž z2=az+b2. Zůstaňme u toho chvilku. Říká se tam, že k řešení této rovnice si nakreslíme nejprve trojúhelník NLM, jehož strana LM se rovná b a strana LN je ˝a. Prodloužíme-li přeponu MN do bodu O tak, aby se ON rovnalo NL, je hledané z rovno OM. (Pokuste se to uvidět, rozumí se jen z podobností nějakých trojúhelníků.) A jestliže pak výsledek zapíšeme (s použitím Pythagorovy věty), dostaneme z=ON+NM=LN+NM=½a+√(¼a2+b2), což je z gymnázia známý vzoreček pro řešení kvadratické rovnice. Chybí tam ono ±, ale záporné kořeny Descarta nezajímají (říká jim ‘nepravé’ a samozřejmě s nimi umí také zacházet), protože jim nemůže odpovídat nějaká délka úsečky. Všechny veličiny (zde a, b) se rozumějí kladné (nebo nulové). Všiměte si také sazečových rozpaků nad dosud nevídanými exponenty; vysázel je prostě do samostatného řádku.
Vraťme se ještě jednou k středním úměrným. Někdy v letech 1619 až 1621 přišel Descartes na následující zařízení (třeba je to ono “invention admirable″ z 10. listopadu 1620):
Pravítko YZ je pevné, pravítko YX se může otáček kolem kloubu Y. K pravítku YX je v bodě B kolmo připevněno další pravítko. Kdyby nebylo už nic dalšího, opisoval by bod B při otáčení tohoto pravítka kružnici BA. Jenže je tam další pravítko DC ve tvaru L, které se posouvá po pevném pravítku tím, jak je postrkováno pravítkem BC. Bod D přitom opisuje nějakou další křivku. A toto pravítko postrkuje (tentokrát po otočném pravítku) další pravítko DE, které postrkuje pravítko EF, přičemž bod F opisuje zase jinou křivku. A tak dále dle libosti. Jestliže si označíte známé úsečky YA=YB=a a v případě první křivky veličiny neznámé: YC=x, CD=y, můžete se pokusit vypočítat jen na základě úměrností a Pythagorovy věty rovnici první křivky. (Mělo by vám vyjít x4=a2(x2+y2); kdyby se někdo pokusil nalézt rovnici druhé křivky, při YE=x, EF=y, měl by dostat x8=a2(x2+y2)3; pro třetí křivku pak x12=a2(x2+y2)5 atd. Možná jste si uvědomili, že x a y jsou zde ‘kartézské souřadnice’ bodu křivky. Pravoúhlé souřadnice sice jsou po Descartovi pojmenovány, ale jeho vynálezem nejsou; souřadnice už znali Řekové a používali je i matematici v době před Descartem. Také není správné připisovat Descartovi objev analytické geometrie; ta se už v nějaké podobě také vyskytovala dříve. Decartes tomu však dal jednotný rámec a udělal daleko víc: položil základy algebraické geometrie – systematického studia algebraických křivek, tj. křivek, jejichž rovnice jsou vyjádřeny polynomy v proměnných x a y (tak jako jsme to právě viděli na křivkách Descartova přístroje).
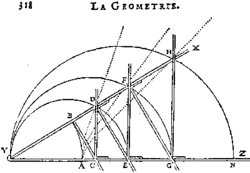 A tohoto zařízení můžeme použít k nalezení tolika středních úměrných, kolika se nám zachce. Poslechněte si Descartův výklad ze začátku třetí knihy Geometrie: ‘Chceme-li totiž nalézt dvě střední úměrné mezi YA a YE, stačí opsat kružnici, jejíž průměr je YE: a protože tato kružnice protíná křivku AD v bodě D, je YD jednou z hledaných středních úměrných. Důkaz toho je vidět ihned pouhým přiložením tohoto nástroje na úsečku YD: neboť jak YA, tak YB, která je jí rovna, se má k YC tak, jako YC k YD a YD k YE. Právě tak k tomu, abychom nalezli čtyři střední úměrné mezi YA a YG, nebo abychom jich nalezli šest mezi YA a YN, stačí jen vést kružnici YFG, protínající AF v bodě F, která stanoví úsečku YF, která je jednou z těchto čtyř středních úměrných; nebo YHN, protínající AH v bodě H, stanoví jednu ze šesti; a tak i pro ostatní.’
A tohoto zařízení můžeme použít k nalezení tolika středních úměrných, kolika se nám zachce. Poslechněte si Descartův výklad ze začátku třetí knihy Geometrie: ‘Chceme-li totiž nalézt dvě střední úměrné mezi YA a YE, stačí opsat kružnici, jejíž průměr je YE: a protože tato kružnice protíná křivku AD v bodě D, je YD jednou z hledaných středních úměrných. Důkaz toho je vidět ihned pouhým přiložením tohoto nástroje na úsečku YD: neboť jak YA, tak YB, která je jí rovna, se má k YC tak, jako YC k YD a YD k YE. Právě tak k tomu, abychom nalezli čtyři střední úměrné mezi YA a YG, nebo abychom jich nalezli šest mezi YA a YN, stačí jen vést kružnici YFG, protínající AF v bodě F, která stanoví úsečku YF, která je jednou z těchto čtyř středních úměrných; nebo YHN, protínající AH v bodě H, stanoví jednu ze šesti; a tak i pro ostatní.’
K nalezení jedné střední úměrné nám stačí pravítko a kružítko. K nalezení dvou středních úměrných to nestačí a potřebujeme nějakou kuželosečku (křivku druhého stupně), k nalezení většího počtu středních úměrných pak křivky vyšších stupňů. Podstatné zde je to, že křivky, kterých zde používáme, jsou všechny algebraické, tj. jsou vyjádřeny pomocí polynomu v proměnných x a y. Jsou však úlohy, kde algebraické křivky nestačí, například známá kvadratura kruhu: k dané kružnici máme sestrojit úsečku, jejíž délka bude rovna délce kružnice. Tuto úlohu nejenže nelze vyřešit pomocí pravítka a kružítka (tj. pomocí úseček a kružnic), ale ani pomocí žádné křivky, která by byla algebraická. Řekové tuto úlohu řešili například pomocí křivky, které říkali kvadratrix. Tato křivka se liší od algebraických tím, že je opisována průsečíkem dvou přímek, jejichž pohyby jsou na sobě nezávislé. Algebraické křivky naproti tomu jsou opisovány průsečíkem přímek, jejichž pohyby jsou vynuceny (‘mechanicky’) pohybem jedné z nich – jako tomu bylo třeba u ‘pravítkového’ přístroje. To byl jeden z velkých Descartových objevů, který byl plně doceněn až v 19. století. Zkoumáním křivek a jim odpovídajících rovnic, což je vlastní obsah Geometrie, otevřel Descartes cestu k moderní ‘vyšší’ matematice. Bezprostředně na něj navázal Newton, který své slavné zákony odvodil právě metodami geometrickými.
Nebudu se u toho zde dále zdržovat, jak píše na mnoha místech Descartes, který zpravidla pokračuje: jednak mne to nudí, jednak nechci psát tak tlusté knihy jako moji předchůdci, a především chci ponechat čtenáři potěšení, aby si to prozkoumal sám; neboť tato kniha má sloužit především ke šlechtění lidského ducha. Když to dobře dopadne, budeme mít na konci semestru komentovaný samizdatový překlad Descartovy Geometrie. A když to dopadne ještě lépe, pak byste si jej mohli i přečíst.


























