Když Davidové zastavují Goliáše

Že se Slunce otáčí kolem své osy, bylo jasné již Galileovi na počátku 17. století, hned poté, co zamířil své primitivní dalekohledy na denní hvězdu a spatřil na ní tmavé skvrny. Pozorováními s časovým odstupem zjistil, že skvrny mění svou pozici, a správně usoudil, že jde o objekty „pevně“ spojené s povrchem Slunce, a změna pozice je tedy projevem otáčení slunečního tělesa kolem vlastní osy.

Podivná sluneční rotace

Netrvalo dlouho a Christoph Scheiner, jiný vynikající pozorovatel, si kolem roku 1630 povšiml, že rotační perioda Slunce odvozená pro skvrny nacházející se poblíž slunečního rovníku je kratší než pro skvrny pozorované dále od rovníku (obr. 2). Tento jev, označovaný jako diferenciální rotace, dále studovali jiní pečliví sluneční pozorovatelé, za všechny jmenujme např. Richarda Carringtona, Gustava Spörera nebo manžele Annie Russell a Waltera Maunderovy. R. Carrington zavedl pro Slunce pevný souřadnicový systém, jehož rotační rychlost odpovídá střední rotační rychlosti odvozené od pohybu slunečních skvrn. Dodnes nese jeho jméno (carringtonovské souřadnice: heliografická šířka a délka) a je základním souřadnicovým systémem používaným k popisu pozice jevů na Slunci. V důsledku diferenciální rotace se však jevy vůči tomuto pevnému systému pohybují – v okolí rovníku rychleji, dále od rovníku pomaleji.¹⁾ Rotaci Slunce lze ale měřit i jinak než výpočtem ze změny polohy objektů. Jednou z význačných metod je metoda spektroskopická. Využívá toho, že disk Slunce má poměrně velký zdánlivý rozměr (kolem půl stupně), a tudíž lze štěrbinou spektrografu se zdánlivým rozměrem několik obloukových vteřin prostorově izolovat určité místo na disku a měřit v tomto místě průmět rychlosti materiálu (plazmatu) do směru k pozorovateli prostřednictvím Dopplerova jevu. Celkový pohyb materiálu bude složen jednak z náhodných pohybů, vyvolaných zejména turbulentní konvekcí, ale také z pohybů systematických, v nichž bude převažovat rotace tělesa. Takto lze určit dopplerovskou složku rychlosti po celém slunečním disku a vhodným zpracováním stanovit křivku rotační.²⁾

Ve skutečnosti je to vše ještě složitější. Klíčem k pochopení jevů je často vzájemné porovnání. Bylo zjištěno, že rotační profily získané různými metodami se významně liší, i pokud jsou určeny pro stejný časový okamžik. Obecně se dá říci, že zdánlivě nejrychlejší rotaci lze odvodit trasováním dopplerovských struktur, pomalejší z měření změn poloh skvrn nebo koncentrovaných magnetických polí a nejpomalejší lze získat spektroskopickou metodou. Dále v případě sledování objektů obecně platí, že čím je objekt prostorově rozlehlejší, tím je zjištěný diferenciální rotační profil plošší, tedy velké objekty (jako pozaďová magnetická pole nebo velké koronální struktury) rotují více jako tuhé těleso. Tradičně byly tyto rozdíly vysvětlovány jako efekt hloubky ukotvení jednotlivých struktur v nitru Slunce, a různé rotační profily byly tedy používány pro sondáž hloubkového profilu rotace.³⁾

Rotace uvnitř

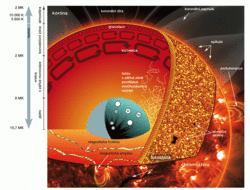
Vnitřní rotaci lze odvodit i jinou metodou: helioseismologií. Ta spočívá v interpretaci šíření seismických vln slunečním nitrem, jejichž projevy, tzv. oscilace, jsou rutinně pozorovány na slunečním povrchu. Helioseismologie je jedinou metodou, která umožňuje sondáž slunečního nitra, a měření rychlosti proudění plazmatu patří mezi již tradiční disciplíny, pro něž je helioseismologie velmi vhodná (obr. 1).

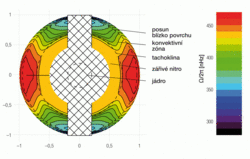Helioseismická pozorování jednak potvrzují šířkovou diferenciální rotaci přípovrchových vrstev, ale odhalují i komplikovanou strukturu hloubkové rotace, jež je pro zvolenou konstantní šířku také diferenciální. Současná měření naznačují, že zářivé nitro Slunce, tedy jeho jádro a vrstva v zářivé rovnováze, rotují víceméně jako tuhé těleso, a to úhlovou rychlostí, jejíž hodnota leží mezi úhlovou rychlostí povrchové rotace na rovníku a u pólů. Na rozhraní vrstvy v zářivé rovnováze a konvektivní zóny se charakter rotace náhle, snad ve vrstvě několika stovek kilometrů, prudce mění. Tato přechodová vrstva se označuje jako tachoklina a podle současného paradigmatu se právě v ní generuje magnetické pole Slunce.

Přípovrchová konvektivní zóna pak podléhá komplikované diferenciální rotaci jak v šířce, tak v hloubce, přičemž kuželové plochy stejné úhlové rotační rychlosti svírají s rovníkem přibližně úhel 25 stupňů. Pro zvolenou konstantní heliografickou šířku tedy úhlová rotační rychlost roste se vzdáleností od středu slunečního tělesa (obr. 3).

Podivné přípovrchové zpomalování

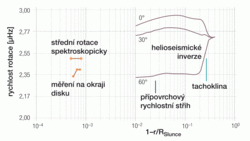
To platí až do přibližně 95 % slunečního poloměru, kdy průběh úhlové rotační rychlosti se vzdáleností od středu začíná klesat a sestupný trend zůstává až k povrchovým vrstvám. Mluvíme o tzv. přípovrchovém rychlostním střihu. Tento trend byl potvrzen nezávislými metodami a mnozí sluneční fyzikové jeho faktickou existenci využívají při vysvětlení různých rotačních profilů získaných různými metodami. Rychlejší rotaci magnetických struktur v porovnání se spektroskopickým profilem tak lze přirozeně vysvětlit jako efekt „zakořenění“ magnetických polí hlouběji, v místech s větší úhlovou rotační rychlostí.⁴⁾

Přípovrchový rychlostní střih bylo velmi obtížné vysvětlit, neboť jeho faktická existence znamená zpomalování povrchových vrstev, a něco z těchto vrstev tedy musí odnášet moment hybnosti.

Teoretické modely jsou dnes schopny rámcově reprodukovat komplikovanou rotaci Slunce správně. Tyto hydrodynamické modely vycházejí ze složité součinnosti rotace viskózního prostředí a turbulentní konvekce, problémy jim však činí přípovrchový střih.

Fotonová spolupráce

Zde je třeba dodat, že helioseismická měření jsou zatížena neurčitostí v přesné lokalizaci, lépe řečeno jsou helioseismicky určené veličiny prostorovým průměrem reálné veličiny přes určitou oblast popsanou průměrovacím jádrem, o němž doufáme, že je dostatečně úzké. V řeči povrchových veličin pak „dostatečně úzké“ znamená ne užší než 2500 km, neboť právě tolik je typická vlnová délka seismických vln v povrchových vrstvách, která určuje efektivní rozlišení.

Jeff Kuhn z Havajské univerzity se svým týmem navrhli průlomovou metodu, jak popsat průběh přípovrchového střihu s lepším vertikálním rozlišením. Využili měření z nejmodernějšího synoptického slunečního dalekohledu, kterým je přístroj Helioseismic and Magnetic Imager (HMI) na palubě kosmické Solar Dynamics Observatory (SDO). Tento přístroj pořizuje celodiskové snímky Slunce s kadencí 45 sekund v šesti pozicích (vzájemně vzdálených 7 pm) spektrální čáry neutrálního železa s klidovou vlnovou délkou 617,334 nm. Každý z bodů profilu této spektrální čáry vzniká v jiné hloubce fotosféry, efektivně tak jednotlivé pozice v čáře postihují tři hloubky v rozsahu přibližně 150 km, v nichž se tato spektrální čára formuje. V těchto třech hloubkách, konkrétně 20, 80 a 156 km nad úrovní, kde se atmosféra stává opticky tlustou, pak vyšetřovali chování slunečních oscilací a z něj odvozovali rotační rychlost dané vrstvy. To nelze udělat pro libovolné místo slunečního disku. Nejlépe se pro to hodí jeho okraj, kde se tyto vrstvy, v nichž se formují dané části spektrální čáry, nepřekrývají.

Jeff Kuhn má s pečlivým studiem slunečního okraje velké zkušenosti. Už v roce 2000 publikoval v Nature článek [2], v němž ohlásil objev zvláštního typu slunečních oscilací, tzv. r-modů, jejichž výskyt se očekává v rotující vrstvě podléhající turbulentní konvekci. V zemské atmosféře jsou r-mody, známé též pod názvem Rossbyho vlny, odpovědné za relativně pravidelné změny počasí v Evropě (kde v průměru platí, že se každé tři dny charakter počasí změní). Tým Jeffa Kuhna tedy identifikoval na Slunci r-mody jako pravidelné zvlnění slunečního okraje, a to s amplitudou 100 m (!) s vlnovou délkou kolem 90 000 km. Detekce 100m zvlnění disku s poloměrem 969 000 km je jistě úctyhodný výkon vyžadující velmi přesnou metodologii. A to tehdy ještě sluneční fyzikové museli vyjít z měření přístrojem Michelson Doppler Imager (MDI) na Solar and Heliospheric Observatory (SOHO) s menší časovou kadencí (60 s), čtyřnásobně horším prostorovým rozlišením a mnohem menším časovým pokrytím, než má HMI/SDO.

Vraťme se však do současnosti. Ve svém článku zveřejněném v Physical Review Letters [3] tým pod vedením Jeffa Kuhna odvozuje, že povrchový rychlostní střih je ve skutečnosti mnohem prudší, než by se zdálo z helioseismických měření. Je zajímavé, že se tento střih objevuje ve vrstvách, které začínají být opticky průhledné, a z nichž tedy mohou unikat fotony do okolního prostoru. Ihned se nabízí myšlenka, zda by za zpomalování povrchu nemohly být odpovědné tyto unikající fotony – přece jen odnášejí určitý moment hybnosti a vyvolávají tak zdánlivou brzdnou sílu. Pro tento model také sestavili příslušné fyzikální rovnice.

Je zajímavé, že tyto rovnice ve výsledku připomínají Poyntingův-Robertsonův efekt působení slunečního záření na prachové částice v jeho okolí, který vede k jejich zpomalování, a tedy postupnému pádu na Slunce. Dlužno podotknout, že předpokládaný odnos momentu hybnosti fotony je vlastně makroskopický relativistický efekt a výsledná anizotropie záření by měla pro pozorovatele na Zemi znamenat, že Slunce je na východním okraji teplejší než na okraji západním. Podle předpovědi Jeffa Kuhna o 0,08 kelvinu…

Zastav í fotony Slunce zcela?

Teplotní rozdíl obou slunečních okrajů tedy asi změřit nepůjde. Na podporu hypotézy je zde další shoda, možná ovšem souhra náhod. Pokud se uváží celková ztráta momentu hybnosti mechanismem navrženým Jeffem Kuhnem za životnost Slunce, odpovídá tato ztráta velmi dobře deficitu momentu hybnosti přípovrchového střihu oproti monotónnímu rotačnímu profilu konzistentnímu s profilem hlubších vrstev konvektivní zóny.

Z rovnic fotonového brždění lze odhadnout i rozdíl ztráty momentu hybnosti pro různé heliografické šířky, a tím i směrnici mocninné funkce ω ~ rα. Opět až překvapivě lze odvodit, že v rovníkových oblastech bude α = −1 s rostoucí hodnotou k větším vzdálenostem od rovníku. Předpověď fotonového brždění tedy není nekonzistentní s pozorováními.

Nabízí se otázka, jak bude brždění povrchových vrstev pokračovat a zda se dá očekávat, že zastaví sluneční rotaci zcela. Autoři odhadují, že pro Slunce je odnos momentu hybnosti fotony jen malým efektem, a vliv na celkovou rotační periodu Slunce je tedy minimální. Aby se brždění projevilo měřitelným zpomalením Slunce – Goliáše – musely by fotony – Davidové – trpělivě odnášet své díly momentu hybnosti po dobu mnohokrát delší, než je stáří vesmíru. Situace ale může být jiná pro hmotné hvězdy, jejichž zářivé obálky jsou daleko rozlehlejší, a fotony tedy unikají z většího objemu hvězdy. Lze proto očekávat, že hmotnější hvězdy by měly mít přípovrchový rychlostní střih mnohem výraznější.

Hypotéza publikovaná astronomy pod vedením Jeffa Kuhna je sice lákavá, ale v tuto chvíli čistě spekulativní a zmíněný „soulad čísel“ může být pouhou souhrou náhod. Na druhou stranu je nabízené vysvětlení v souladu s dostupnými pozorováními a jeho správnost je testovatelná u jiných hvězd.