Dynamika lavín

Určite ste si všimli, že niektoré deje v prírode a spoločnosti sa šíria lavínovitým spôsobom. Ak je niekde v populácii zvýšená koncentrácia chrípkových vírusov, možno očakávať lavínovitý vzrast ochorení, ba až chrípkovú epidémiu. Ak príliš dlho husto sneží, na istom mieste strmého svahu sa naruší stabilita snehovej prikrývky a môže padnúť jedna, alebo aj viac lavín. Pomalé posuvy v zemskej kôre môžu viesť až k ničivým zemetraseniam, pomalé procesy v ekonomike ku ekonomickým krízam a dlhodobá nespokojnosť a frustrácie obyvateľov k revolúciám.

Lavínovité procesy prebiehajú podľa jednotného scenára. Vo veľkom, mnohozložkovom dynamickom systéme (ekologickom, spoločenskom, fyzikálnom...) sa najprv dlho akoby nič nedeje. Hoci vždy prebiehajú nejaké procesy, pôsobia nejaké sily a spätne ovplyvňujú dynamický systém, pomalé lokálne zmeny sa javia ako nedôležité, ba až bezvýznamné, a ich dôsledky sa zdanlivo dajú odvrátiť rôznymi drobnými úpravami a opatreniami. Na prvý pohľad je systém stabilný a v poriadku.

Avšak nie je tomu tak. Pomalé procesy spôsobia, že v systéme postupne narastá „teplota“, zväčšuje sa počet nestabilných stavov, rastie náchylnosť systému ku kríze. Ibaže nevieme dňa ani hodiny... A potom to zrazu príde. Stačí malý, nedôležitý podnet a spustí sa lavína, ktorá znovu, v krátkom čase, obnoví stabilitu.

Lavína môže byť malá; tá zasiahne len nepatrnú časť systému, ale za istých podmienok nastane proces globálneho rázu. Niektoré štruktúry systému sú nadobro zmetené z povrchu zemského (napr. vyhynutie druhov v ekológii), iné, nové naopak vyvstanú...

V roku 1982 prišli traja fyzici, Per Bak, Chao Tang a Kurt Wiesenfeld s teóriou, ktorá sa zaoberá dynamikou lavínovitých procesov. V odbornej terminológii sa jej hovorí teória samoorganizovaného kritického stavu. Je to doteraz najkompletnejší popis nelineárnych, priestorovo rozľahlých dynamických systémov, pozostávajúcich z veľkého množstva prakticky identických elementov. Jednotlivé elementy spolu interagujú na krátke vzdialenosti, čo znamená, že cítia, a ovplyvňujú len svojich najbližších susedov. (Spojenie „najbližší sused“ nemusí nutne znamenať blízkosť priestorovú. Častokrát sa jedná o najbližšieho suseda v zmysle interakcie. Napríklad v ekosystéme druhy, ktoré si nekonkurujú, sa výrazne neovplyvňujú, aj keď žijú v tej istej lokalite. A naopak, druhy zviazané trebárs potravinovým reťazcom, komunikujú aj na väčšie priestorové vzdialenosti.)

Ako príklad takéhoto dynamického systému môže slúžiť ľudské spoločenstvo. Je to systém silne nelineárny; všetci vieme, že reakcia spoločnosti často nie je priamoúmerná podnetu. Ak skúmame globálne vlastnosti spoločnosti, môžeme abstrahovať od indivídua a zaviesť akéhosi štatisticky priemerného občana, ktorého kontakty s inými členmi spoločenstva sa obmedzujú viac–menej na pár priateľov a známych.

Podstatu teórie samoorganizovaného kritického stavu si ozrejmíme na dvoch príkladoch. Prvým je piesková kopa a druhým hypotetický úrad, plný nervóznych úradníkov. Predstavme si stôl a na ňom rozhodených zopár hrstí suchého piesku. To sú počiatočné podmienky nášho myšlienkového pokusu. Prikladaním zrniečok na náhodne vybraté pozície piesková kopa rastie. Týmto simulujeme pomalé, vekovité procesy v prírode. Ako zrniek pribúda, stále častejšie sa stane, že jedno zrnko padne na druhé. Vytvoria sa tak lokálne nestability, ktoré opäť zanikajú za pomoci lavíniek. Lavínky sú najprv malé; jedno alebo zopár zrniečok sa skotúľa nižšie. Ale ako sa sklon kopy blíži ku kritickej hodnote, ktorú už nemôže prekročiť, zvyšuje sa pravdepodobnosť veľkej lavíny, zasahujúcej podstatnú časť kopy. Hovoríme, že systém sa blíži k samoorganizovanému kritickému stavu. V samoorganizovanom kritickom stave priloženie jediného zrniečka piesku môže spustiť lavínu zasahujúcu prakticky celý systém.

V druhom príklade si predstavme veľký úrad s množstvom pracovníkov sediacich v radoch vedľa seba (obr. 1). Každý z nich má štyroch najbližších susedov. Poslíček prináša spisy a náhodne ich rozdeľuje na stoly (pomaly pôsobiace prírodné sily). Úradníci sú leniví a v podstate nikdy nespracujú ani jeden spis. Každý z nich má ale nejaký prah tolerancie počtu spisov na stole. Nech je tento prah pre všetkých uradníkov rovnaký – tri spisy. Ak sa náhodou stane, že priložený spis je už štvrtý v poradí, pracovník zrazu prepadne panike a posunie všetky štyri spisy na stoly svojich najbližších susedov (krátkodosahové interakcie). Ak niektorí z nich už majú pred sebou tri spisy a dostanú štvrtý, rozčúlia sa, opäť rozhodia spisy na stoly najbližších susedov a celý proces lavínovite pokračuje ďalej. Ak lavína dospeje až k úradníkom sediacim pri okne, tí jednoducho vyhodia niektoré spisy von na ulicu (otvorené hraničné podmienky)...

Ak na počiatku náhodne rozdelíme isté množstvo spisov na stoly úradníkov, konečný výsledok pokusu nebude závisieť od toho, ako ich rozložíme, ba dokonca ani vtedy nie, ak na počiatku budú stoly úplne prázdne. Náš dynamický systém, zložený z nervóznych úradníkov (podobne ako kopa piesku), nie je totiž citlivý na počiatočné podmienky.

V oboch príkladoch súhrou pomalého budenia dynamického systému, rýchlej relaxácie – lavíny a hra-ničných podmienok sa ustanoví samoorganizovaný kritický stav, s typickým kritickým pravdepodobnostným rozdelením veľkostí lavín v tvare mocninného zákona. Samoorganizovaný kritický stav je stacionárny stav, do ktorého systém po určitom čase dospeje pod vplyvom lokálnych dynamických zákonov, bez ohľadu na počiatočné podmienky.

Spúšťacím mechanizmom lavíny je prekročenie istej lokálnej podmienky stability, napr. lokálneho kritického sklonu kopy v prvom príklade, či lokálnej kritickej výšky stĺpca spisov v príklade druhom. To, aká lavína v tej ktorej chvíli padne, závisí od momentálnych podmienok v systéme, od jeho histórie, neurčitostí, šumov apod. Keby sme niektorý zo zmienených pokusov opakovali niekoľkokrát, trebárs so zmenenými počiatočnými podmienkami, a monitorovali pri tom veľkosti lavín v čase, zistili by sme, že výsledok bude rovnaký, ale len štatisticky. Pravdepodobnosti malých i veľkých lavín budú dané tým istým typickým pravdepodobnostným rozložením. Avšak súslednosť jednotlivých udalostí nijako nie je možné zopakovať ani v tom najprecíznejšie postavenom experimente. Nepodarí sa nám totiž presne skontrolovať polohu všetkých zrniek, klimatické podmienky, teplotu vzduchu apod. A v nelineárnych systémoch aj tá najmenšia neurčitosť môže mať veľmi výrazný vplyv.

Aké podmienky musia byť splnené, aby sa systém sám zorganizoval do kritického stavu? Zhrňme: Dynamický systém (kopa piesku, nervózni úradníci, ekosystém, zemská kôra…) musí pozostávať z veľkého množstva krátkodosahovo interagujúcich elementov, ktoré možno považovať za identické. Dôležitou podmienkou je schopnosť dynamického systému do istej miery vzdorovať lokálnym poruchám. Vážnu rolu hrá aj diferencia v časových škálach. Schopnosť vzdorovať poruchám je v našich príkladoch reprezentovaná kritickými prahmi pre lokálny sklon kopy (lavína sa spustí, ak je na istom mieste kopy svah príliš strmý), či lokálnou výškou stĺpca spisov.

Diferencovanie časových škál znamená, že proces budenia systému (tj. prikladanie pieskových zrniek, spisov…) je extrémne pomalý vzhľadom na trvanie relaxačného procesu – lavíny. Lavínou sa opäť ustanoví rovnováha.

Súhrou všetkých týchto faktorov systém dospeje do stacionárneho stavu, to značí do stavu dynamickej rovnováhy medzi budením a relaxáciou. Voláme ho samoorganizovaným kritickým stavom.

Pre lepšie porozumenie dynamike lavín si každý môže doma urobiť jednoduchý pokus. Je to vlastne experiment, ktorý vlani umožnil fyzikom z Univerzity v Oslo potvrdiť teoreticky predpovedané vlastnosti samoorganizovaného kritického stavu.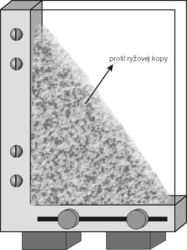

Vezmeme dve sklenené platne a dve hliníkové tyče a zložíme ich tak ako na obr. 2. Celé zariadenie upevníme do stojana. Platne majú byť od seba vzdialené asi 5 milimetrov. Potom do štrbiny, tesne k okraju s prekážkou z hliníkovej tyče, pridávame postupne po jednom zrniečka podlhovastej ryže. Naša „jednorozmerná“ ryžová kopa pomaly rastie. Začínajú sa spúšťať malé lavínky. Prebytočná ryža prepadáva otvoreným okrajom von. V kritickom stave, s kritickým globálnym sklonom, môžeme pozorovať lavíny všetkých veľkostí; jediným obmedzením veľkosti lavíny je rozmer experimentálneho zariadenia.

Teória samoorganizovaného kritického stavu bola prvýkrát úspešne použitá pri štúdiu pohybov zemskej kôry. Dokázala objasniť empiricky známy Gutenbergov-Richterov zákon, dávajúci do funkčného vzťahu energiu zemetrasení a početnosť zemetrasení danej energie. Na všetkých seizmicky aktívnych miestach zemeguľe je tento funkčný vzťah rovnaký, typický pre systémy so samoorganizovaným kritickým stavom. Zemetrasenie je takto vnímané ako lavínovitý, krátkodobý proces, ktorý je dôsledkom pomalých, dlhodobých pohybov zemskej kôry.

Aj v biológii má možno teória samoorganizovaného kritického stavu svoje opodstatnenie. Evolucionisti vedia, že v istých, relatívne krátkych periódach, dochádzalo k prudkému evolučnému pohybu, vývoju nových a zániku starých druhov. Zároveň sa objavilo množstvo zmien u druhov prežívajúcich. Tieto obdobia boli nasledované dlhými periódami relatívneho evolučného pokoja, keď sa nič veľkého nedialo. V biológii tento jav popisuje teória „prerušuvaných rovnováh“. Dánski fyzici Per Bak a Kim Sneppen vytvorili prednedávnom jednoduchý evolučný model, tzv. Bak – Sneppenov model, na ktorom ukázali, že jav „prerušovaných rovnováh“ je možno dôsledkom samoorganizovaného kritického stavu v biosystémoch.

Teória samoorganizovaného kritického stavu ukazuje, že za katastrofickými procesmi v prírode i spoločnosti nemusia byť nutne veľké globálne poruchy. Stačí aj malý lokálny podnet, aj ten v nelineárnom mnohozložkovom systéme môže vyvolať nečakanú odozvu. Veľké i malé otrasy v prírode i spoločnosti sú dôsledkom tých istých pomalých procesov. Všetko je do času, všetko sa raz skončí a žiadne lokálne úpravy a „snehové bariéry“ nezabránia pádu veľkej lavíny, pokiaľ ovšem neprestane „snežiť“. A príroda sa už sama stará, aby „snežilo“...