Výpočty pomocou nukleových kyselín

Už i školák vie, že výpočty majú rôznu zložitosť. Sčítanie považujeme za jednoduchšie ako násobenie. Príčina je v tom, že násobenie vyžaduje viac námahy než sčítanie. Presnejšie, na vynásobenie dvoch n-ciferných čísiel potrebujeme približne n² krokov (elementárnych operácií), kdežto sčítanie ich vyžaduje iba ~ n. Všetko sa dá sformulovať oveľa precíznejšie. Namiesto školáka alebo bežného počítača odborníci používajú idealizovaný počítač, ktorý vymyslel už pred vyše 60 rokmi Alan Turing. Tento počítač je tvorený, v tej najjednoduchšej forme, jednou dlhou páskou rozdelenou na políčka a hlavicou. Na každom políčku pásky je zapísaný nejaký symbol. V jednom kroku dokáže hlavica prečítať symbol z políčka, na ktorom je nastavená, prepísať ho na iný a posunúť sa o jedno políčko doprava alebo doľava. Dôležité je, že na tomto tzv. Turingovom stroji je možné robiť tie isté výpočty, ako povedzme na najnovšom počítači značky Cray. Výpočtovú zložitosť teraz môžeme formalizovať ako počet krokov, ktoré musí urobiť Turingov stroj na výpočet daného problému. Už spomínané sčítanie a násobenie patrí do tzv. P-triedy výpočtovej zložitosti, ktorá je charakteristická tým, že počet krokov N potrebných na výpočet daného problému je daný ako polynóm od parametra veľkosti vstupu n (keďže nás zaujímajú “veľké vstupy″, stačí sa obmedziť na najvyššiu mocninu tohto polynómu)

N ~ n^r,

kde r je konštanta. Do P-triedy patrí okrem násobenia a sčítania aj násobenie dvoch n × n matíc, pre ktoré platí

N ~ n³ ,

a tisíce ďalších výpočtových problémov. Existujú však i problémy zložitejšie. Uvažujme napr. známy problém obchodného cestujúceho, ktorý má za úlohu navštíviť n miest, tak aby jeho cesta bola najkratšia možná. Najjednoduchším spôsobom riešenia takejto úlohy je nájsť všetky možné cesty, spočítať ich dĺžku a zistiť, ktorá z nich je najkratšia. Problém je však v tom, že počet možných ciest je rovný počtu všetkých permutácií n miest, ktorých je n!. Takže počet krokov, ktoré vyžaduje riešenie úlohy týmto spôsobom, je

N ~ n! rovná se přibližně nⁿ .

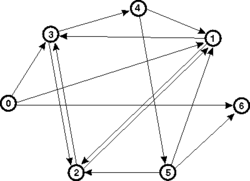Toto je samozrejme tá najhoršia metóda, ako riešiť problém obchodného cestujúceho. Existujú aj lepšie prístupy, ale vždy je počet krokov exponenciálne veľký, napr. približne 2ⁿ. Problémy tohto typu patria do tzv. NP-triedy výpočtovej zložitosti. Vráťme se ešte na chvíľu k násobeniu. Školácky algoritmus vyžaduje na riešenie n² krokov. V 60. rokoch sa podarilo prekvapivo Karacubovi objaviť algoritmus, ktorý vyžaduje iba n^1,6 krokov, a dokonca Schönhage ukázal, že na jeho strojoch (trochu odlišných od Turingových) násobenie je rovnako zložité ako sčítanie a vyžaduje n elementárnych operácií. Vzniká teda otázka, či sa raz nepodarí objaviť polynomiálny algoritmus na riešenie problému obchodného cestujúceho. Radi by sme na túto otázku odpovedali, je to však snáď najväčší otvorený problém teoretickej informatiky. Väčšina odborníkov je presvedčená, že je to nemožné a že problém obchodného cestujúceho, ako i celú triedu tzv. NP-úplných problémov nebude nikdy možné riešiť polynomiálnymi algoritmami. Na ilustráciu porovnajme n² polynomiálny algoritmus a 2ⁿ exponenciálny algoritmus. Nech pre n=10 potrebujú obidva na rozriešenie problému 1s, potom na rozriešenie problému s n = 100 potrebuje prvý 100 s, avšak druhý až 10¹⁴ rokov. (Pozn. red.: Vek vesmíru je odhadovaný rádovo na 10¹⁰ roků.) Vzhľadom k tomu, že do NP-triedy patria mnohé dôležité problémy, každý efektívny algoritmus ich riešenia vyvolá mimoriadny záujem. Rovnako to bolo i s prácou Leonarda M. Adlemana uverejnenou koncom minulého roku (Science 266, 1021 – 1024, 1995). Adleman je známy počítačový teoretik z Kalifornskej univerzity v Los Angeles a preto boli mnohí prekvapení, že sa v jeho práci objavujú fotografie výsledkov gelovej elektroforézy, experimentálne protokoly a podobné veci, ktoré sa bežne vyskytujú v prácach venovaných napr. klonovaniu DNA, a snáď si v prvom momente mysleli, že i v takom prestížnom časopise môže úradovať “tlačiarenský škriatok″. Nie je to však pravda. Adleman navrhol nový spôsob riešenia NP-úplných výpočtových problémov pomocou genetických manipulácií. Svoju metódu ilustroval riešením problému “hľadania hamiltonovskej cesty v orientovanom grafe″. Študovaný graf je na obrázku, a ako vidíme, skladá sa z vrcholov pospájaných hranami, na ktorých je zadaná šípkou ich orientácia. Pre orientovaný graf so vstupným vrcholom v_in a výstupným vrcholom v_out existuje hamiltonovská cesta vtedy, ak existuje postupnosť vrcholov a hrán, ktorá spája vstupný a výstupný vrchol, pričom každý vrchol je v nej práve raz. Na obrázku s v_in = 0 a v_out = 6 je to postupnosť 0→1→2→3→4→5→6. V prípade takéhoto jednoduchého grafu je samozrejme ľahké rozhodnúť, či má hamiltonovskú cestu. Pre väčšie grafy je to však problém značne zložitejší a vyžaduje exponenciálny počet krokov.

Adlemanov postup možno zosumarizovať do 4 bodov:

1. Vygenerovať náhodnú cestu grafom.
2. O cestách, ktoré nezačínajú vo v_in a nekončia vo v_out, ďalej neuvažovať.
3. Ak má graf n-vrcholov, uvažovať iba o cestách, ktoré prechádzajú presne n-vrcholmi, a to každým vrcholom práve raz.
4. Ak nejaká cesta zvýšila, potom hamiltonovská cesta existuje, v opačnom prípade nie.

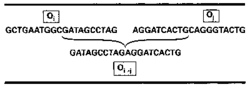
Adleman každému vrcholu i v grafe priradil oligomér O_i nukleovej kyseliny o dĺžke 20 nukleotidov, pričom ich postupnosť bola vybraná náhodne (pretože máme 4 druhy nukleotidov, počet možností je 4²⁰, a je teda málo pravdepodobné, aby rôzne vrcholy mali podobné sekvencie). Pre každú hranu i,j grafu bol nasyntetizovaný oligonukleotid O_i,j spôsobom, ktorý je zrejmý z nasledovnej schémy

V prípade i=0 a i=6 (vstupný a výstupný vrchol cesty) boli ako O_0,i a O_i,6 použité priamo O₀ a O₆. Takáto konštrukcia zachováva orientáciu hrán (O_i,j sa nerovná O_j,i). Oligomér komplementárny (v zmysle Watsona a Cricka) ku O_i si označíme ako Ok_i. A teraz môžeme prejsť k popisu vlastných experimentov (detailný popis je v citovanom článku). Pre každý vrchol v grafe (okrem vstupného a výstupného) a pre každú hranu bolo navzájom zmiešaných 50 pmol Ok_i a 50 pmol O_i,j. Ok_i oligonukleotidy slúžili ako svorky, ktoré spojili dohromady oligonukleotidy patriace susedným hranám. Takže ligačná reakcia viedla ku vzniku DNA molekúl, ktoré kódovali cesty grafom. V ďalšom kroku bola použitá polymerázová reťazová reakcia (PCR), kde ako priméry boli použité oligonukleotidy O₀ a Ok₆ (podrobnosti PCR metódy sú v článku Š. Vilčeka, Vesmír 69, 309, 1990/6).

Takýmto spôsobom boli “namnožené″ cesty, ktoré začínali vo vrchole 0 a končili vo vrchole 6. Grafy, ktoré obsahovali práve 7 vrcholov, boli izolované pomocou elektroforézy, kde boli identifikované ako pás zodpovedajúci 140 párom nukleotidov. Na izoláciu ciest grafom, ktoré prechádzali každým vrcholom práve raz, bol použitý systém magnetických guličiek s naviazanými oligonukleotidmi Ok₁ až Ok₅. Reťazce DNA boli denaturáciou najprv navzájom rozdelené a potom sa postupne izolovali jednoreťazcové polynukleotidy, ktoré obsahovali aspoň jeden vrchol č. 1, v ďalšom kroku aspoň jeden vrchol č. 2 atď., až po vrchol č. 5. Ako výsledok sa získali nukeové kyseliny, ktoré kódovali hamiltonovskú cestu grafom. Sekvenovaním danej nukleovej kyseliny sa následne získala aj postupnosť vrcholov. Kľúčovým princípom úžasnej efektívnosti danej metódy je enormný paralelizmus ligačnej reakcie, veď počas prvého kroku prebehlo 10¹⁴ ligácií. Tento počet môže byť použitím mikromolárnych množstiev zvýšený až na 10²⁰. Na porovnanie, bežné počítače pracujú rýchlosťou 10⁶ operácií za sekundu a najrýchlejšie superpočítače rýchlosťou 10¹² operácií za sekundu. Naviac, v DNA je informácia odpovedajúca 1 bitu uložená v objeme 1 nm³, kým napr. vo videokazetách 1 bit zodpovedá 10¹² nm³. Metóda sa môže na prvý pohľad zdať dosť kuriózna, takou však zo začiatku bola aj metóda simulovaného žíhania navrhnutá V. Černým pred 12 rokmi na základe analógií so štatistickou fyzikou, ktorá je dnes jedným z najmocnejších nástrojov na riešenie zložitých optimalizačných problémov. Ďalšie rozvinutie Adlemanovho prístupu, s využitím aj iných enzymatických reakcií, ktoré sa zúčastňujú transkripcie, translácie a ďalších procesov, súvisiacich so spracovaním nukleových kyselín v bunke, možno povedie k tomu, že počítač budúcnosti bude tvorený nukleovou kyselinou a enzýmami, ktoré spracovávajú informáciu v nej zakódovanú.

Aby sme boli verní odkazu J. A. Komenského, ktorý chcel, aby učenie bolo hrou, dovoľujeme si na záver zadať čitateľovi úlohu: “Navrhnite spôsob riešenia problému obchodného cestujúceho pomocou Adlemanovej metódy.″