Konstruování z hmoty a děr

Příroda své výtvory zdokonaluje (optimalizuje) už stamiliony let a dospěla k obdivuhodným výsledkům. Zdánlivě všední stéblo trávy je skutečně zdařilou víceúčelovou konstrukcí. Také lidská díla se vyvíjejí k stále větší účelnosti, jejich návrhy však musí vznikat nepoměrně rychleji. Konstruktér už dávno nepostupuje metodou pokusu a omylu, ale musí vědomě směřovat k předem stanovenému cíli.

Každý si jistě dovede představit práci konstruktéra, k níž po generace patřilo rýsovací prkno a nyní jeho úlohu stále více přejímá počítač, který slouží nejen ku geometrickému znázornění konstrukce, nýbrž i k výpočtům vlastností navrhovaného objektu. Konstrukcí rozumíme i jednotlivé stavební nebo strojní díly.

Bylo by možné na počítač přenést i tu fázi konstruování, která se doposud odehrávala v technikově hlavě? Může počítač vystihnout základní rysy, jež konstrukce musí mít, aby vyhověla nárokům na únosnost, efektivní využití materiálu apod.?

Pro jednoduchost se omezme na statické problémy nezávislé na čase, tj. konstrukce zatížené neměnnými silami.

Ukazuje se, že pokud se smíříme s jistými zjednodušeními, lze úspěšně automatizovat i tento první krok návrhářské práce, a to postupy, v nichž hlavní roli hrají matematická fyzika, aplikovaná matematická analýza a numerická matematika. Klíčovým pojmem, jemuž se za chvíli budeme věnovat podrobněji, je topologická optimalizace.

V problému topologické optimalizace jde o přibližné stanovení těch míst, v nichž se materiál soustředí (kde bude více „hmoty“ a méně „děr“). Protože se vychází ze stejnoměrně rozložené „prahmoty“, která se v průběhu času zhušťuje v nosných částech konstrukce a mizí z oblastí pro konstrukci málo významných, celý postup připomíná koncentraci hmoty v protoplanetární mlhovině.

Na čem je založena konstrukční kondenzace hmoty

Než učeně odpovíme, že na lokální homogenizaci materiálu, povězme si něco o standardním modelování konstrukcí – mostů, budov, stožárů – i o problémech s tím spjatých.

Před zhotovením konstrukce je třeba spočítat její zatížení a deformace, a dále namáhání konstrukčního materiálu. Existuje řada matematických modelů umožňujících předvídat chování konstrukce. Důležitou roli v nich hrají materiálové konstanty. Technicky založený čtenář si možná vzpomene na Youngův modul pružnosti (tj. konstantu vystupující ve vztahu udávajícím, o kolik se prodlouží zatížená tyč). Počet konstant závisí na daném materiálu a modelu. Například ocel je nejčastěji charakterizována dvěma konstantami.

Při sestavování modelu konstrukce je výhodné opírat se o bilanci práce, kterou koná síla zatěžující těleso, a deformační energie, která se v zatěžovaném tělese nashromáždí. Takto definovaný problém většinou neumíme vyřešit přímo, tj. metodou „tužka a papír“. Můžeme jej však nahradit úlohou, která je mu blízká a kterou dokážeme, většinou s pomocí počítače, vyřešit. Obvykle postupujeme tak, že v konstrukci zvolíme konečný počet jistých významných bodů a chování celé konstrukce odvodíme z chování v těchto bodech. Tomuto kroku se říká diskretizace, často používanou diskretizační metodou je metoda konečných prvků (viz Vesmír 71, 377, 1992/7).

Diskretizačních metod a jejich aplikací je mnoho, nicméně někdy se můžeme dostat do úzkých už při volbě diskretizačního kroku. To je (přibližná) vzdálenost mezi oněmi zvolenými význačnými body, kterou odhadneme podle toho, jak velké jsou detaily v konstrukci.

Představme si modelový příklad. Mějme krychli o hraně jednoho metru vyrobenou z houbovitého materiálu, který se vyznačuje rovnoměrně rozmístěnými vzduchovými „bublinami“ o průměru jednoho milimetru, jež jsou od sebe vzdáleny také zhruba milimetr. Milimetrové detaily nás nutí zvolit aspoň 1000 × 1000 × 1000 diskretizačních bodů. Pod zatížením se každý zvolený bod může posunout. Posunutí ve směru jednotlivých prostorových os musíme vypočítat. Model diskretizovaný tímto způsobem tedy vede zhruba ke třem miliardám lineárních algebraických rovnic pro tři miliardy neznámých, což je velké sousto i pro současné nejvýkonnější počítače. Uvedený příklad není zcela akademický, pomysleme např. na kost, konstrukční prvek přírody. Většina kostí sice nemá metrové rozměry, ale zato má velmi jemnou strukturu, tudíž by bylo nutno zvolit mnoho význačných bodů.

Jemné diskretizaci se však lze vyhnout tím, že určíme materiálové konstanty kosti jako takové. Ty samozřejmě budou závislé na poměru kostní hmoty („trámků“ oddělujících „dutinky“) a „dutinek“, a též na tvaru „trámků“, a tudíž i na tvaru „dutinek“.

Materiálové charakteristiky kosti můžeme změřit v laboratoři. Pro nás ovšem bude podstatné, že ze znalosti geometrie „dutinek“ a „trámků“ kostní hmoty a materiálových konstant kostní hmoty můžeme vypočítat materiálové konstanty kosti jako kompozitního materiálu. To je úkolem teorie homogenizace, hovoříme o homogenizovaném materiálu.

Objekt z homogenizovaného materiálu lze diskretizovat pomocí menšího počtu bodů. (U výše zmíněné krychle by šlo řádově o tisíce.)

Obecněji můžeme uvažovat o kompozitním materiálu, v němž mikrooblasti nejsou vyplněny vzduchem, ale jiným homogenním materiálem. Jako příklad uveďme beton, v němž vlastně roli zmíněných vzduchových bublin přejímají oblázky. Při výpočtu nemůžeme použít materiálové konstanty jednotlivých oblázků a zrnek písku, ale musíme použít předpokládané průměrné konstanty betonu jako takového. Zajímají nás makroskopické vlastnosti homogenizovaného materiálu, i když jeho struktura je heterogenní.

Topologická optimalizace na příkladu leteckého nosníku

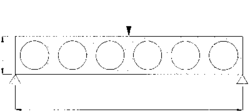
Na praktickém příkladu si ukážeme, jak při návrhu konstrukčního dílu může postupovat konstruktér opírající se o moderní výpočetní metody. Představme si letecký nosník (obrázek). Je to vlastně kovový obdélník s odlehčovacími otvory, jimiž procházejí kabely a potrubí. Naším úkolem je navrhnout nosník optimální, nosník s minimální hmotností, jehož materiál však nebude namáhán více než u standardního nosníku z obrázku.

Základní myšlenka konstrukce optimálního nosníku spočívá ve dvou hlavních krocích. Zprvu vyjdeme z obdélníkového nosníku bez velkých otvorů, avšak „vyrobeného“ (ovšem jen jako matematický model) ze speciálního kompozitu – z rovnoměrně porézního materiálu. Inkluze („dírky“) necháme nakynout tam, kde zvýšená pórovitost nevadí. 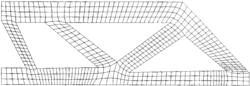A naopak kompozitní materiál zahustíme zmenšením inkluzí v těch místech, která jsou pro nosnou funkci nosníku podstatná. Vysoká pórovitost bude znamenat, že materiál můžeme zcela odstranit – vznikne větší otvor, průvlek. Druhým krokem pak bude upřesnění hranic takto vzniklých otvorů.

Podívejme se podrobněji na to, jak je předchozí plán prakticky realizován. Díky symetrii se konstruktér může zabývat jen polovinou nosníku a tím si ušetřit část práce. Musí ovšem úlohu trochu přeformulovat. Místo zatěžující síly uprostřed nosníku (obrázek) uvažuje reakci podpory v jeho pravém dolním rohu (obrázek) a pohyb bodů na ose symetrie buď omezí jen na vertikální směr (trojúhelníčky s „kolečky“), nebo zcela vyloučí (černý trojúhelníček).

Obrázek znázorňuje výchozí situaci při topologické optimalizaci. Úzký tmavý pruh lemující tři strany obdélníka vyjadřuje požadavek, aby materiál na okraji nosníku měl maximální hustotu, to znamená žádné inkluze. Zbylá část obdélníka je vyplněna kompozitním materiálem se stejnou pórovitostí, tj. s rovnoměrně rozloženými inkluzemi.

Z předchozího výkladu o homogenizaci víme, že ze znalosti lokální pórovitosti lze vypočítat lokální hodnoty materiálových konstant, ty dosadit do modelu nosníku, a pak spočítat deformaci a namáhání nosníku.

Pro přehlednost a též z výpočetních důvodů si výchozí obdélník rozdělíme na čtvercová nebo obdélníková pole (obrázek), říká se jim prvky. Každý prvek je tvořen kompozitním materiálem s jistou pórovitostí. V průběhu výpočtu se pórovitost prvků bude měnit.

Jak si takový materiál představujeme, to ukazuje obrázek. „Řidší“ materiál má větší inkluze, v „hustším“ materiálu jsou inkluze menší. Každý prvek je charakterizován určitou hustotou materiálu. Zpočátku pro všechny prvky stejnou, ale během chodu optimalizačního algoritmu se zvyšující v těch prvcích, které jsou pro nosník důležité, a naopak se snižující tam, kde materiál není využit.

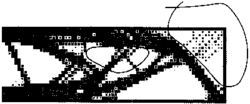
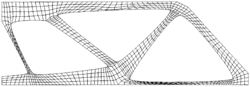Algoritmus topologické optimalizace zmenšující (zvětšující) inkluze tam, kde je účelné, aby materiál houstl (řídl), je dosti složitý a vyžaduje nejen řadu výpočtů, nýbrž i určité matematické přeformulování výchozí úlohy. Jeho výsledkem je (i přes jistou neurčitost) celkem dobrá představa o užitečném rozložení hmoty uvnitř nosníku (obrázek).

Geometrická optimalizace

Této znalosti konstruktér využije v druhém stupni optimalizace – nalezení optimální geometrie. Opíraje se o výsledek topologické optimalizace navrhne výchozí konstrukci z konkrétního technického materiálu (např. oceli, duralu apod.), nikoli z abstraktního porézního kompozitu. Geometrická optimalizace si klade za cíl pouze „vylepšit“ tvar konstrukce. Obvykle není dovoleno, aby se spojovaly, popřípadě zacelovaly otvory obsažené ve výchozím návrhu, či dokonce vznikaly otvory další.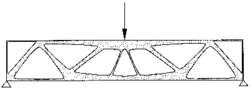

Protože každý otvor je vlastně dán křivkou své hranice, konstruktér potřebuje najít optimální tvar těchto křivek. Definuje je tedy prostřednictvím nějakých geometrických parametrů, a jeho úkolem pak je nalézt jejich optimální hodnoty.

Z technických důvodů musí mít nosník obdélníkový obrys, i když horní rohová část k jeho nosné funkci přispívá jen málo. Aby byl další výpočet jednodušší, rohová část se dočasně neuvažuje, viz obrázek, obrázek. Konstrukce je opět rozdělena na prvky, tentokrát méně pravidelného tvaru, materiál prvku je teď ovšem pevně dán a neměnný. Mění se jen hranice otvoru, což implikuje i změnu velikosti a tvaru prvků.

Optimální tvar poloviny nosníku vidíme na obrázku, celý optimalizovaný nosník na obrázku. Ve srovnání se standardně vyráběným nosníkem (obrázek) je optimalizovaný nosník o 42 % lehčí, přičemž namáhání materiálu vzrostlo jen o zanedbatelná 4 %.

Přestože spojení topologické a geometrické optimalizace má již řadu konkrétních aplikačních výsledků, lidským konstruktérům prozatím vyhynutí nehrozí. Topologická optimalizace se z univerzitních pracovišť šíří do průmyslové praxe jen pomalu. Pokročilejší vývoj lze pozorovat v optimalizaci geometrické, pro niž již existuje nejeden komerční počítačový program. Stále je však nutné mít na zřeteli, že sebelepší software určený k řešení tak složitých úloh se neobejde bez věci znalé obsluhy. ^{1) 2)}