O prostoru, o času a o fyzice
Tři Hawkingovy a tři Penrosovy přednášky jsou určeny čtenářům se zájmem o kvantovou fyziku, teorii polí, kosmologické problémy okolo černých a bílých děr, velkého třesku a velkého zhroucení (pozn. red.: Jiří Grygar zavádí pro Big Crunch český překlad velký křach), antropického principu, aplikace kvantové teorie na vesmír i strunovou teorii a twistorový pohled na časoprostor. Názory autorů se v řadě otázek liší. Vyvrcholením diskuse je sedmá kapitola, kde jsou názorové odlišnosti formulovány explicitně. Jejich přístup k poznání je odlišný. Hawking je, podle vlastního mínění, pozitivistou a úkolem vědy podle něj je umět předpovídat výsledky experimentů. Svého partnera označuje za platonika, Penrose pro sebe raději volí přívlastek realista. Dejme však – podobně jako recenzenti časopisu Scientific American – slovo autorům v několika ukázkách ze samotné knihy, která je trochu náročnější než vybrané ukázky a vyžaduje alespoň elementární znalost relativistické fyziky. Zdeněk Kalva
STEPHEN HAWKING, ROGER PENROSE: The Nature of Space and Time.
Princeton University Press 1996, řada „Isac Newton Institute Series of Lectures“, 141 stran
Zdá se, že kvantová teorie černých děr ... vede k nové úrovni nepředpovídatelnosti ve fyzice za obvyklou neurčitost spojenou s kvantovou mechanikou. Je to proto, že černé díry mají vnitřní entropii a ztrácejí informaci o naší oblasti vesmíru. Chtěl bych říci, že tato tvrzení jsou kontroverzní: Mnozí lidé zabývající se kvantovou gravitací včetně téměř všech, kteří k ní přešli od fyziky elementárních částic, by instinktivně zavrhli myšlenku, že informace o kvantovém stavu systému mohou být ztraceny. Avšak neuspěli příliš v tom, aby ukázali, jak se informace může z černé díry dostat. Věřím, že nakonec budou muset přijmout můj návrh, že informace je ztracena, právě tak jako byli nuceni souhlasit s tím, že černé díry vyzařují, což bylo proti všem jejich předsudkům...Skutečnost, že gravitace je přitažlivá, znamená, že má snahu stahovat hmotu ve vesmíru dohromady a tvořit objekty, jako jsou hvězdy a galaxie. Ty se po nějakou dobu mohou bránit dalšímu smršťování tepelným tlakem (v případě hvězd), nebo rotací a vnitřními pohyby (v případě galaxií). Avšak nakonec teplo nebo úhlový moment jsou odneseny a objekt se začne smršťovat. Jestliže hmota je menší než asi 1,5 hmoty Slunce, může být smršťování zastaveno tlakem degenerovaného plynu elektronů nebo neutronů. Z objektu se stane bílý trpaslík nebo neutronová hvězda. Jestliže však má hmotu větší než tato mez, neexistuje nic, co by mohlo smršťování zastavit. Jakmile se smršťí na určitou kritickou velikost, gravitační pole na jeho povrchu bude tak silné, že světelný kužel bude ohnut zpět... Mohli byste dokonce vidět, že světelné paprsky směrem ven se ohýbají tak, že se sbíhají a ne rozbíhají. To znamená, že existuje uzavřený povrch....
Musí tedy existovat oblast prostoročasu, z níž není možné uniknout do nekonečna. Této oblasti říkáme černá díra. Její hranice se nazývá horizont událostí; je to tzv. nulová plocha tvořená světelnými paprsky, kterým se nezdařilo uniknout do nekonečna... 
Když těleso kolabuje a vzniká černá díra, mnoho informací se ztrácí. Kolabující těleso je popsáno velkým množstvím parametrů. To je např. materiál, který je tvoří, a multipólové momenty rozložení hmot. Přesto však vytvořená černá díra je zcela nezávislá na tom, z čeho vznikla, a rychle ztrácí všechny multipólové momenty s výjimkou prvních dvou: monopólového momentu (což je hmota) a dipólového momentu (což je moment hybnosti).
Tato ztráta informace v klasické teorii nevadí. Můžeme říci, že všechna informace o kolabujícím tělese je ještě uvnitř černé díry. Pro pozorovatele mimo černou díru by bylo velmi těžké určit, jaké bylo kolabující těleso. Avšak v klasické teorii to bylo v principu možné. Pozorovatel ve skutečnosti nikdy nepřestane vidět povrch kolabujícího tělesa. Jak se povrch bude blížit horizontu událostí, bude se pozorovateli jevit matněji a jeho kolaps čím dál tím pomalejší. Pozorovatel však stále může vidět z čeho se skládá a jak je hmota rozložena.
V kvantové teorii je to všechno jinak. Kolabující těleso by vyslalo jen určitý počet fotonů, než překročí horizont událostí. Ty nepostačí k tomu, aby odnesly veškerou informaci o kolabujícím tělese. To znamená, že v kvantové teorii neexistuje pro vnějšího pozorovatele způsob, jak měřit stav kolabujícího tělesa. Mohli byste si myslet, že to nehraje velkou roli, protože informace by byla ještě uvnitř černé díry, přestože ji nemůžeme zvnějšku měřit. Ale teď se uplatňuje další rys kvantové teorie černých děr... Podle kvantové teorie černá díra vyzařuje a ztrácí hmotu. Zdá se, že nakonec zcela zmizí a s ní všechna informace uvnitř. Ukazuji, že tato informace je skutečně ztracena a v žádné formě se nenavrátí. Ukážu, že tato ztráta informace zavádí novou úroveň neurčitosti spojenou s kvantovou teorií. Naneštěstí, na rozdíl od Heisenbergova principu neurčitosti, bude tato úroveň neurčitosti obtížně potvrditelná experimentálně.
Velké fyzikální teorie 20. století jsou kvantová teorie, speciální teorie relativity, obecná teorie relativity a kvantová teorie pole. Tyto teorie nejsou nezávislé: obecná teorie relativity byla vybudována na speciální teorii relativity, kvantová teorie pole má jako svůj vstup speciální relativitu a kvantovou teorii.Říká se, že kvantová teorie je nejpřesnější fyzikální teorií všech dob, neboť její přesnost je řádu 1:1011. Chtěl bych však podotknout, že obecná relativita byla testována s přesností 1:1014 (a že tato přesnost je zřejmě omezena pouze přesností pozemských hodin). Mluvím o binárním pulzaru PSR 1913+16 – dvojici vzájemně se obíhajících neutronových hvězd, z nichž jedna je pulzarem. Obecná relativita předpovídá, že se tyto dráhy pomalu rozpadají (a že perioda se zkracuje), protože emisí gravitačních vln se ztrácí energie (pozn. red.: viz M. Plavec: Druhá Nobelova cena pulzarům, Vesmír 72, 665, 1993/12; J. Niederle: Nobelova cena za fyziku, Vesmír 73, 11, 1994/1). To bylo skutečně pozorováno a celý popis pohybu za období 20 let ... souhlasí s obecnou relativitou (která podle mne zahrnuje newtonovskou teorii) s pozoruhodnou přesností zmíněnou výše... Kvantoví teoretici si vždy činili nárok na to, aby se obecná relativita přizpůsobila jejich teorii, neboť ta je přesná. Já se domnívám, že to je kvantová teorie pole, která má co dohánět.
Ačkoli tyto čtyři teorie jsou pozoruhodně úspěšné, mají své problémy... Obecná relativita předpovídá existenci prostoročasových singularit. V kvantové teorii existuje „problém měření“... Je možné, že řešení různých problémů těchto teorií spočívá v tom, že tyto teorie samy nejsou úplné. Například mnozí teoretici anticipují, že kvantová teorie pole by mohla nějakým způsobem „vymazat“ singularity z obecné relativity ...
Rád bych se zmínil o ztrátě informace v černých dírách, která souvisí s posledním problémem. Souhlasím téměř se vším, co o tom řekl Stephen Hawking. Ale zatímco Stephen se dívá na ztrátu informace způsobenou černými dírami jako na další neurčitost ve fyzice, která je nad neurčitostí kvantové teorie, já ji pokládám za „komplementární“ neurčitost... Je možné, že nepatrně informace unikne v okamžiku vypaření černé díry ... ale tento nepatrný zisk informace je mnohem menší než ztráta informace při kolapsu [...]
Jestliže v myšlenkovém experimentu uzavřeme systém do obrovské krabice, můžeme uvažovat, jak se jeví vývoj hmoty v této krabici z hlediska popisu ve fázovém prostoru 1) . V oblasti fázového prostoru odpovídající situaci, v níž je přítomna černá díra, budou trajektorie fyzikálního vývoje stále blíže a objemy sledující tyto trajektorie se budou smršťovat. To je způsobeno ztrátou informace v černé díře. Toto smršťování je v přímém rozporu s jednou poučkou, větou, zákonem klasické mechaniky s Liouvillovým teorémem, který říká, že objemy ve fázovém prostoru zůstávají konstantní....
Takže prostoročas černé díry porušuje tento teorém. Já na to pohlížím tak, že ztráta objemu ve fázovém prostoru je vyvážena procesem „spontánního“ kvantového měření, v němž informace se získává a objem fázového prostoru roste. Proto pokládám neurčitost způsobenou ztrátou informace v černé díře za „komplementární“ k neurčitosti kvantové teorie: jedna je odvrácenou stranou druhé...
Uvažujme myšlenkový experiment Schrödingerovy kočky. Popisuje situaci kočky v krabici, v níž foton dopadá na polopropustné zrcadlo a propuštěný foton dopadne na detektor. Jestliže detektor zaznamená foton, automaticky spustí revolver, který zastřelí kočku. Jestliže detektor foton nezaznamená, kočka zůstává živá. (Vím, že Stephen Hawking by nesouhlasil takto zneužívat kočku, byť v myšlenkovém experimentu.) Vlnová funkce systému je superpozicí těchto dvou možností... Proč však nám naše vnímání nedovoluje vnímat makroskopickou superpozici takovýchto stavů namísto pouhých makroskopických alternativ „kočka je mrtvá“ a „kočka je živá“?...
Předpokládám, že něco nefunguje se superpozicí alternativních prostoročasových geometrií, které by se objevily, kdyby byla zahrnuta obecná relativita. Možná superpozice dvou různých geometrií není stabilní a rozpadá se do dvou alternativ. Příkladem geometrií by mohly být prostoročas živé kočky nebo prostoročas mrtvé kočky. Nazývám tento rozpad do jedné NEBO druhé možnosti objektivní redukcí, což se mi obzvláště zamlouvá pro příhodný akronym (OR). Jak se k tomu vztahuje Planckova délka 10–33 cm? Kritérium přírody určující, kdy jsou dvě geometrie podstatně rozdílné, by záviselo na Planckově délce a ta určuje časové měřítko, v němž se objevuje redukce do různých alternativ. 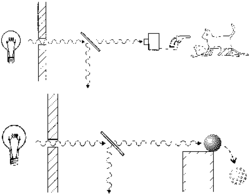
Lokální zákony fyzikálních polí jsou časově symetrické, přesněji jsou CPT invariantní. Pozorovaný rozdíl mezi minulým a budoucím musí tedy pocházet z okrajových podmínek vesmíru. Předpokládejme, že vesmír je prostorově uzavřený a že expanduje do své maximální velikosti a pak opět kolabuje. Jak Roger Penrose zdůraznil, vesmír bude velmi rozdílný na obou koncích této historie. Na tom konci, kterému říkáme počátek vesmíru, se zdá být velmi hladký a pravidelný. Když však opět kolabuje, očekáváme, že je velmi neuspořádaný a nepravidelný. Protože však existuje mnohem více neuspořádaných konfigurací než uspořádaných, znamená to, že počáteční podmínky by měly být vybrány neuvěřitelně přesně.
Zdá se tedy, že okrajové podmínky na těchto dvou koncích času musí být velmi rozdílné. Roger navrhuje, že na jednom z konců času by Weylův tenzor měl vymizet, na druhém však nikoli. Weylův tenzor je ta část křivosti prostoročasu, která není v Einsteinových rovnicích lokálně určena hmotou. Měl by být malý v hladkých uspořádaných raných stadiích, avšak veliký v kolabujícím vesmíru. Takže tento návrh rozlišuje oba konce vesmíru a tak by mohl vysvětlit směr času.
Domnívám se, že tento návrh je weylovský více než v jednom smyslu slova. Zaprvé není CPT 2) invariantní. Penrose v tom vidí přednost, já cítím, že bychom se neměli vzdávat symetrií, pokud k tomu nejsou závažné důvody. Zadruhé jestliže by byl Weylův tenzor přesně nula v raném vesmíru, byl by přesně homogenní a izotropní a zůstal by takový po všecek čas. Penrosova hypotéza o Weylově tenzoru by nemohla vysvětlit fluktuace pozadí ani poruchy, které vedly ke vzniku galaxií a těles, jako jsme my sami.
Přes to všechno se domnívám, že Penrose poukázal na důležitý rozdíl mezi oběma konci času. Avšak fakt, že Weylův tenzor byl velmi malý na jednom konci času, by neměl být kladen jako ad hoc okrajová podmínka, ale měl by být odvozen z obecnějšího principu ...
Jak mohou být oba konce času rozdílné? Proč by měly být poruchy na jednom konci malé a na druhém ne? Důvod je, že existují dvě možná komplexní řešení rovnic pole... Jedno řešení odpovídá jednomu konci času, druhé druhému... Na jednom konci času je vesmír hladký a Weylův tenzor je velmi malý. Nemohl však být přesná nula, neboť to by porušovalo princip neurčitosti. Místo toho měly existovat malé fluktuace, které se později dostaly do těles, jako jsou naše galaxie a tělesa jako my. A naopak vesmír na druhém konci času by měl být velmi nepravidelný a chaotický s Weylovým tenzorem velikým. To by vysvětlovalo pozorovaný směr času i to, proč šálky padají ze stolů a rozbíjejí se spíše, než by se skládaly a vyskakovaly zpátky na stůl.
Z toho, jak chápu Hawkingovu pozici, se nedomnívám, že se v otázce hypotézy Weylova tenzoru lišíme příliš. Pro počáteční singularitu je Weylova křivost přibližně nulová... Hawking argumentuje, že musí existovat malé kvantové fluktuace v počátečním stavu a tak poukazuje na to, že hypotéza o nulovosti Weylovy křivosti počáteční singularity je klasická, a existuje tudíž jistá pružnost v přesném znění Weylovy hypotézy. Z mého hlediska jsou malé fluktuace přijatelné, zejména v kvantovém případě. Potřebujeme pouze něco, aby byly blízké nule...Hartleův a Hawkingův návrh na vesmír bez okrajových podmínek je dobrým kandidátem pro strukturu počátečního stavu. Zdá se mi však, že pro vyrovnání se s koncovým stavem potřebujeme něco velmi odlišného. Konkrétně teorie, která vysvětluje strukturu singularit, by měla porušovat [CPT a jiné symetrie], aby něco z podstaty hypotézy Weylovy křivosti mohlo vzniknout. Toto porušení časové symetrie by mohlo být docela subtilní; mělo by být implicitně v pravidlech teorie, která pokročí za kvantovou mechaniku. 
Roger cítí, že ... kolaps vlnové funkce zavádí do fyziky narušení CPT symetrie. Vidí toto narušení přinejmenším ve dvou situacích: v kosmologii a v černých dírách. Souhlasím s tím, že můžeme vnést časovou asymetrii způsobem, jakým klademe otázky o pozorováních. Avšak úplně zavrhuji myšlenku, že existuje nějaký fyzikální proces, který odpovídá redukci vlnové funkce nebo který má cokoli do činění s kvantovou gravitací či s vědomím. To mi zní jako magie, nikoli jako věda.
Kvantová mechnika existuje kolem 75 let. To není tak dlouho, srovnáváme-li to např. s Newtonovou teorií gravitace. Nepřekvapilo by mne tudíž, jestliže by kvantová mechnika měla být modifikována pro makroskopické objekty.Na začátku této diskuse S. Hawking uvedl, že on je pozitivista, zatímco já jsem platonik. Těší mne, že je pozitivista, ale myslím si, že podstatné je, že já jsem spíše realista. Jestliže tedy srovnáváme naši diskusi se slavnou diskusí Bohra a Einsteina před nějakými 70 lety, domníval bych se, že S. Hawking hraje roli Bohra, zatímco já hraji roli Einsteina! Einstein totiž argumentoval, že by mělo existovat cosi jako reálný svět, nikoli nutně představovaný vlnovou funkcí, zatímco Bohr zdůrazňoval, že vlnová funkce nepopisuje „reálný“ mikrosvět, ale pouze naší „znalost“ užitečnou pro předpovídání.
Mělo se za to, že Bohr v této diskusi uspěl. Ve skutečnosti Einstein od roku 1925 „zabodoval“ také (podle Paisovy biografie Einsteina). Je vskutku pravda, že k pokroku kvantové teorie nepřispěl ničím velikým, i když jeho kriticizmus byl velice užitečný. Domnívám se, že důvod, proč Einstein nepřispěl k pokroku kvantové teorie, spočíval v tom, co kvantové teorii scházelo. Touto scházející složkou bylo záření černé díry objevené Stephenem Hawkingem o 50 let později. Je to tato ztráta informace spojená se zářením černé díry, co poskytuje nový impulz.
Poznámky
První Fridmanovo řešení z roku 1922 zahrnovalo vlastně celou třídu modelů, jejichž společnou vlastností byla prostorová uzavřenost (konečnost) vesmíru. Takové vesmíry měly v minulosti časový počátek, od něhož začíná prostorová expanze, jež se však v průběhu doby zvolňuje, až se posléze na krátký okamžik zastaví a poté přejde ve smršťování. To se naopak bude s časem zrychlovat, až se vesmír zhroutí do hmotného bodu a zanikne. Této závěrečné singularitě se někdy říká velký křach, na rozdíl od velkého třesku na počátku. Matematicky jsou tyto modely charakterizovány geometrickou veličinou zvanou křivost. Společnou vlastností uzavřených modelů je kladná křivost +1 (sférické modely). To znamená, že v tomto prostoru je součet úhlů v trojúhelníku vždy větší než 180o; prostor je tedy neeuklidovský a k jeho popisu musíme používat Riemannovu geometrii (daným bodem v prostoru nelze vést ani jednu rovnoběžku k dané přímce). Přestože uzavřené vesmíry jsou prostorově konečné [mají v každém okamžiku konečný objem, úměrný výrazu (1 +z)3], nemají žádnou hranici v žádném směru nenarazíme nikdy na neprostupnou zeď.
Obvyklá laická otázka: Když je vesmír konečný, tak co je za ním?″ vychází z chybné představy, že uzavřený vesmír má euklidovskou geometrii. V křivém Riemannově vesmíru můžeme letět, rovně″ libovolně dlouho v nejhorším případě se znovu dostaneme na místo, kde jsme svou pouť započali. V uzavřených modelech vesmíru jsme zkrátka v situaci mravence, který leze po zemském glóbu bez omezení a jistě netuší, že má k lezení jen omezenou (konečnou) plochu.
Jednotlivé uzavřené modely se od sebe liší celkovou délkou trvání. Mohou existovat třeba jen nepatrný zlomek sekundy, ale také stamiliardy let. O tom rozhoduje měřitelná veličina zvaná decelerační parametr (parametr zpomalení expanze). Udává se hodnotou q, která pro uzavřené modely vesmíru je vždy větší než +0,5 (čím je q větší, tím kratší je trvání takového vesmíru). Tuto třídu modelů nezávisle objevil roku 1927 belgický kosmolog Georges Lemaître.
Druhé Fridmanovo řešení Einsteinových rovnic, publikované roku 1924, zahrnuje opět celou třídu modelů, jejichž společnou vlastností však je prostorová otevřenost (nekonečnost) vesmíru. Vesmíry tohoto typu počítají opět s časovým počátkem (velkým třeskem), avšak na rozdíl od předešlé třídy modelů nemají časový konec:
Rozpínají se neustále nade všechny meze (škálový faktor je stále větší než 1 ). Nicméně vlastní gravitace hmoty vesmíru způsobuje, že i zde se rozpínání zpomaluje, což se vyjadřuje deceleračním parametrem q, v tomto případě menším než +0,5 (avšak větším než 0).
Společnou vlastností otevřených Fridmanových modelů je záporná křivost 1 (hyperbolické modely). To znamená, že v takových modelech vesmíru je součet úhlů v dostatečně velkých trojúhelnících měřitelně menší než 180o; jde tedy opět o prostor neeuklidovský, leč k jeho popisu musíme užívat Gaussovy-Lobačevského-Bolyaiovy geometrie (daným bodem v prostoru lze vést více rovnoběžek k dané přímce). Hyperbolické modely jsou prostorově nekonečné už od okamžiku velkého třesku (což si stěží umíme představit) a navždy takové zůstávají. Jediným konečným rysem je jejich časový počátek.
Mezi oběma třídami Fridmanových modelů (každá třída obsahuje nekonečnou množinu modelů) leží jeden mezní model, propočítaný roku 1932 společně Albertem Einsteinem a holandským kosmologem Willemem de Sitterem. (Albert Einstein původně nepřijal Fridmanovo řešení a domníval se, že Fridman se při odvozování dopustil chyby. V té době totiž Einstein stále ještě žil v zajetí konvenční představy o časově statickém řešení svých rovnic, neboť jedině takový vesmír byl pro něj a většinu jeho současníků představitelný. Teprve na naléhání svých přátel se Einstein znovu zabýval Fridmanovým řešením; uznal, že je správné, a Fridmanovi se veřejně omluvil.) V tomto mezním případě je křivost prostoru rovna nule a k popisu vesmíru lze proto použít klasické euklidovské geometrie. Vesmír tohoto typu je rovněž od okamžiku velkého třesku neustále prostorově nekonečný a rozpíná se trvale nade všechny meze, přičemž však rychlost rozpínání se pozvolna blíží nule. Decelerační parametr q je v tom případě přesně +0,5. Součet úhlů v kosmologických trojúhelnících je vždy přesně 180o (daným bodem v prostoru lze vést jednu rovnoběžku k dané přímce).
Rozdíly mezi jednotlivými třídami modelů lze přiblížit podobenstvím s vrhem kamene vzhůru v zemském gravitačním poli. Zde je důležitým pojmem úniková rychlost (11,2 km/s pro zemský povrch). Jestliže kameni při svislém vrhu udělíme počáteční rychlost nižší, než je úniková, bude se kámen pohybovat vzhůru zpomaleně, až dosáhne horní úvratě, v níž se na okamžik zastaví, a pak bude zrychleně padat zpět k Zemi, na niž dopadne tou rychlostí, kterou byl původně vržen. Let kamene potrvá tím déle, čím blíže byla počáteční rychlost k rychlosti únikové. Jelikož počáteční rychlost se může spojitě měnit, dostáváme tak nekonečnou množinu případů, jejichž výsledkem je vždy kámen dopadnuvší zpět na povrch Země.
Je zřejmé, že podobně se chovají uzavřené Fridmanovy-Lemaîtrovy modely, v nichž je rychlost expanze vesmíru podkritická. Vyznačují se počáteční a koncovou singularitou (kámen na povrchu Země), zpomalujícím se letem vzhůru (období kladných červených posuvů ve spektru galaxií) a zrychlujícím se návratem zpět (období záporných modrých posuvů ve spektrech galaxií).
Jestliže však kámen vypustíme rychlostí nadkritickou (vyšší, než je úniková), bude se natrvalo vzdalovat od Země, byť stále se snižující rychlostí. Let kamene potrvá věčně, podobně jako trvají věčně otevřené Fridmanovy modely se zápornou křivostí. Ve vesmíru budeme neustále pozorovat červené posuvy (kámen i galaxie se trvale vzdalují). V mezním případě je kámen vypuštěn přesně únikovou rychlostí, takže se bude opět stále vzdalovat od Země, třebaže bude jeho rychlost neustále klesat (bude přesně rovna nule v nekonečné vzdálenosti od Země). Tato situace odpovídá kritickému Einsteinovude Sitterovu modelu vesmíru.
Z těchto schematických úvah vyplývají i první návody, jak srovnat modely s pozorováním a nalézt model, jenž se nejlépe shoduje se skutečností. Můžeme měřit dostatečně velké (kosmologické) trojúhelníky a zjišťovat odchylky v součtu úhlů od 180o. Můžeme však také měřit decelerační parametr q pomocí Hubbleova vztahu mezi červeným posuvem a vzdáleností a zjišťovat odchylky od linearity pro velmi velká z. Řekněme rovnou, že tudy cesta nevede. Nejsme totiž s to změřit všechny tři úhly v kosmologických trojúhelnících, neboť neumíme létat do vzdálených galaxií, a v místním okolí je v každém případě geometrie velmi přibližně euklidovská. Rovněž tak neumíme dobře určit odchylky od linearity v Hubbleově vztahu, neboť zejména vzdálenosti velmi vzdálených galaxií a kvasarů známe příliš nepřesně. Jediné, co z současných pozorování plyne, je to, že reálný vesmír se přiliš neliší od kritického Einsteinovade Sitterova modelu.
S ohledem na měřicí chyby se patrně ani v budoucnu nepodaří na otázku vztahu reálného vesmíru vůči Fridmanovým modelům odpovědět lépe. Jak jste jistě postřehli, je hranice mezi oběma třídami modelů (s kladnou a zápornou křivostí) nekonečně tenká představuje ji jediný model s nulovou křivostí. Pozorovací chyby jsou však vždy konečně malé (nelze měřit s nekonečnou přesností). Je-li tedy reálný vesmír dosti blízko kritickému Einsteinovude Sitterovu modelu, budou měricí chyby obsahovat nejistotu, zahrnující jak mírně uzavřené, tak mírně otevřené modely. Navíc hypotéza kosmické inflace přímo předvídá, že reálný vesmír má přesně nulovou křivost.
Ať tak či onak, zmíněná pozorování nám umožňují v dalších úvahách pominout téměř všechny dosud uvažované modely vesmíru (mnohé z nich, nepatřící k žádné třídě Fridmanových řešení, jsem pro jistotu ani neuvedl, abych čtenáři nepřidával nadbytečné starosti) a podrobně rozebrat model jediný, model Einsteinůvde Sitterův. Zřejmě se tak nedopustíme žádné velké chyby. Jedinou výjimkou je krátké období kosmologické inflace, neboť tu musíme popisovat úplně odlišným modelem (de Sitterovým z roku 1917).
Na témata související s fyzikou prostoru a času a s kosmologií vyšly ve Vesmíru tyto stati:
Abramowicz M., Jones B., Karas V., Novikov I.: Bizarní svět černých děr, Vesmír 76, 9, 1997/1
Dovčiak M.: Dobre kŕmená čierná diera, rámeček viz Vesmír 76, 130, 1997/3
Hadrava P.: Rekordní černá díra, Vesmír 74, 251, 1995/5
Hadrava P.: Kosmografické mystérium současnosti, Vesmír 71, 263, 1992/5 a Vesmír 71, 337, 1992/6
Hadrava P.: Velký třesk je v černé díře, Vesmír 70, 165, 1991/3
Grygar J.: Stáří vesmíru, Vesmír 74, 125, 1995/3
Grygar J.: Rekordní červený posuv kvasaru, Vesmír 71, 116, 1992/2
Grygar J.: Poselství o stavu kosmologie, Vesmír 67, 83, 1988/2
Grygar J.: Pád nebo sláva antropického principu, Vesmír 67, 83, 1988/2
Grygar Jiří: Zatímco vesmír stárne, mládne, Vesmír 67, 555, 1988/10
Karas Vl.: Výzkum aktivních galaktických jader, Vesmír 68, 63, 1989/2
Kleczek Josip: Oblasti blízké počátku vesmíru, Vesmír 75, 195, 1996/4
Langer J.: Existuje ještě jiný důkaz rozpínání vesmíru než rudý posun spektrálních čar ve světle vzdálených galaxií? Vesmír 75, 695, 1996/12
Niederle J.: Nobelova cena za fyziku, Vesmír 73, 11, 1994/1
Novotný J.: Kosmologie, rozpínání a relativita, Vesmír 74, 250, 1995/5
Plavec M.: Kvazary po 34 letech, Vesmír 76, 129, 1997/3
Plavec M.: Okénko do nejvzdálenějšího vesmíru, Vesmír 75, 197, 1996/4
Plavec M.: Černá díra obrovská a skoro jistá, Vesmír 74, 91, 1995/2
Plavec M.: Druhá Nobelova cena pulzarům, Vesmír 72, 665, 1993/12
Plavec M.: Jestliže se tato zpráva potvrdí..., Vesmír 71, 294, 1992/5
Podolský J.: Vlny versus částice, Vesmír 71, 193, 1992/4
Semerák O.: Proč je v jádře M87 černá díra? Vesmír 74, 94, 1995/2
Štohl J.: Vek vesmíru veľká neznámá, Vesmír 68, 425, 1989/8




















