Procházka virtuální zahradou
Ano, originální, vzrušující a důležité – pakliže je to pravda… Jak ale poznají, že přírodní algoritmy jsou stejné nebo alespoň podobné těm jejich?
Edward O. Wilson: Konsilience: jednota vědění (s. 99)
Biologie je ta část přírodovědy, která se zabývá živými tvory. Je ale možná škoda, že skoro upadla v zapomenutí dvě krásná česká slova – přírodopis a přírodozpyt. Tuším za nimi odraz sice ne nutně přiznávaného, ale o to reálnějšího rozštěpení přírodovědy, které se dá snadno ukázat právě na poli biologickém.
Biologie obrazů a příběhů
Řekne-li se „přírodopisec“, vybaví se – přinejmenším čtenáři verneovek – poněkud roztržitý a veskrze nepraktický pán, pobíhající po nehostinných exotických krajinách vybaven botanickou torbou, síťkou na motýly, kamerou, nádobíčkem na vycpávání ptáků a tlustým zápisníkem; postava lehce komická, leč vzbuzující zároveň směs obdivu a soucitu. Snad pro vášeň a nadšení, se kterým torbu, herbář, sešit a všeliké skleničky plní doklady, vzorky a záznamy svých nálezů a pozorování. Protože o to mu jde především: pozorovat, fotografovat, sbírat, dokumentovat, pojmenovávat a třídit; uchopit Přírodu (nebo aspoň povodí Zambezi či jednu pramennou stružku na Českomoravské vrchovině) ve veškeré její rozmanitosti a bohatství tvarů, a zachytit ji do jediného obrazu, propracovaného do nejmenších podrobností. Nezajímá ho příliš, jak věci a jevy vznikají a proč jsou takové, jaké jsou: jde mu o to, jak vypadají.Představa, kterou vyvolává slovo „přírodozpyt“, je temnější: Galvani soustředěně pozorující cukající se žabí stehýnka, slintající psi akademika Pavlova, sinalé světélkování smrtelně zářící nádobky na pracovním stole paní Curieové-Skłodowské, hektolitry bakteriálních kultur a hekatomby bílých myší; s obdivem se mísí mrazení – patří sem spíš Frankenstein než Jacques Paganel. Přírodozpytec nepozoruje, ale táže se, vyslýchá, hledá podezřelé – nikoli pachatele, ale mechanizmy. Moc ho nezajímá, jak věci vypadají, protože střeva, diferenciální rovnice a sloupcové grafy zpravidla vypadají jako střeva, rovnice a grafy. Jde mu o zákonitosti a obecnosti, které hýbou molekulami i celou biosférou, o to, odkud se věci a jevy berou, o osnovu příběhů evoluce nebo individuálního vývoje.
Můžeme namítnout, že přírodověda není ani „přírodopis“, ani „přírodozpyt“, protože je obojím dohromady. Že jedním z nejvýznamnějších témat moderní biologie je zkoumání cesty od vaječné buňky k mnohobuněčnému organizmu: hledání „příběhu“ o tom, jak vzniká „obraz“. Ale vezmeme-li do ruky moderní biologickou práci, najdeme zpravidla buď jedno, anebo druhé: buď anatomii, taxonomii, floristiku a faunistiku, nebo fyziologii, ekologii, etologii či vývojovou biologii.
Matematické modely jako nástroj popisu a výkladu
Mají tedy všichni biologové, „přírodopisci“ i „přírodozpytci“, něco společného? Zvykli jsme si, že věda je vědou natolik, nakolik jsou její myšlenky vyjádřitelné řečí matematiky. Jedním z možných sjednocujících prvků by tedy mohlo být používání matematických metod, a především matematických modelů.Matematické modely se uplatňují při popisu kinetiky enzymových reakcí stejně jako při předvídání osudů ekosystémů, při posuzování vzájemné podobnosti tvarů (viz Vesmír 78, 35, 1999/1), při odhadu hodnot fyziologických parametrů z naměřených pokusných dat nebo při vytváření umělých „dat“ v simulovaných virtuálních experimentech. Modely jsou sice vždy založeny na pozorování, ale způsob založení může být rozmanitý. Hezkou ilustrací jsou dva popisy množení mikrobiální populace – logistická křivka a Monodův model (rámeček 1). První model „jen“ extrapoluje data, je jejich obrazem, aniž by se je snažil vykládat; parametry modelu jsou empirické a postrádají přímý fyziologický smysl. Druhý model vychází z konkrétních předpokladů o příčinách pozorovaného dění, a z nich vyvozuje, vykládá, jak by se kultura měla chovat. Chová-li se skutečná kultura tak, jak žádá „fyziologický“ model, znamená to, že předpoklady modelu mohou, ale nemusí být správné. Kultura se chová přibližně stejně dobře i podle modelu „nefyziologického“, který vychází z dosti odlišných předpokladů.
Navzdory tomu přírodozpytec dává zpravidla přednost modelu, jehož parametry může zvěcnit, reifikovat – například přisoudit jim fyziologický smysl. Snad se v tom odráží obecně lidský sklon spatřovat v obecných pojmech skutečné jevy a věci (S. J. Gould) a věřit, že cokoli dostalo jméno, musí být věcí či bytostí nadanou vlastní nezávislou existencí (J. S. Mill). A model, který se nedá lehce reifikovat, se leckdy zdá podezřelým (dokladem budiž třeba motto tohoto článku).
Gramatika rostlinného těla
Mikrobiální kultura není mnohobuněčné tělo. Právě možnost nalezení matematického popisu („obrazu“) prostorových tvarů mnohobuněčných tvorů lze považovat za přesvědčivý doklad toho, že biologie je matematizovatelná. Ke spokojenosti přírodozpytně naladěných biologů by tento popis měl být rovněž reifikovatelný, aspoň tak, jako Monodova růstová křivka.Na první pohled by se zdálo, že struktury živočišných těl lze modelovat snáze než tvary rostlin. Živočichové jsou zpravidla symetričtí a jejich vlastnosti, jako je třeba počet nohou, jsou víceméně stálé. Jejich tělní plán je (geneticky) definován a s výjimkou nešťastných náhod jej prostředí neovlivňuje. Naproti tomu stačí vyhlédnout z okna, abychom si uvědomili nesmírnou rozmanitost tvarů rostlinného světa, která je jen zčásti podmíněna geneticky: dva stromy téhož druhu nikdy nevypadají stejně. Přisedlý způsob života s sebou totiž nese riziko, že rostlina občas o nějaký orgán přijde. Nemá-li to být fatální, nesmí být struktura těla jednoznačně předurčena, musí zůstat prostor pro regeneraci a improvizaci. Instrukce, které vývoj řídí, jsou však nutně omezené co do rozsahu: k dispozici je jen to, co se vejde do genomu.
I když se dva stromy téhož druhu nepodobají jeden druhému jako vejce vejci, podobají se jako modřín modřínu způsobem, jakým se svým tvarem „zacházejí“: stačí mnohdy jediný pohled na siluetu stromu, abychom poznali, jakého je druhu. U dvouděložné dřeviny, jako je jabloň, si můžeme být jisti, že pupeny leží v úžlabí listů, že postavení listů na větvičce je druhově specifické, že z vrcholového pupenu v příštím roce vyraší letorost a že se za určitých podmínek (například když větévka o vrcholový pupen přijde) probudí spící úžlabní pupeny, které pak dají vzniknout letorostům, jež svírají s původní větévkou poměrně přesně vymezený úhel.  Víme také, že některé úžlabní pupeny dávají vzniknout květenství, jehož strukturu lze popsat, a že květy odkvétají a plody zrají. Na rostlinu můžeme pohlížet jako na „stavebnici“ malého počtu typů „stavebních kamenů“ (jako jsou stonky, listy, pupeny, květy a plody), která roste podle malého počtu pravidel. Z toho pak můžeme vycházet při konstrukci matematického modelu – třeba pomocí L-systémů (rámeček 2 a obrázky).
Víme také, že některé úžlabní pupeny dávají vzniknout květenství, jehož strukturu lze popsat, a že květy odkvétají a plody zrají. Na rostlinu můžeme pohlížet jako na „stavebnici“ malého počtu typů „stavebních kamenů“ (jako jsou stonky, listy, pupeny, květy a plody), která roste podle malého počtu pravidel. Z toho pak můžeme vycházet při konstrukci matematického modelu – třeba pomocí L-systémů (rámeček 2 a obrázky).
Rostlinné tvary jsou jen zdánlivě složité, podobně jako tvary fraktálních obrazců (Vesmír 67, 458, 1988/8). Nesmíme jen měřit složitost počtem jehlic modřínu nebo úseček aproximujících obrys Mandelbrotovy množiny. V obou případech je lepší mírou komplexity počet instrukcí nezbytných k modelování tvaru – a ten je až překvapivě malý.
Kolik cest vede k cíli
Abychom věrohodně modelovali rostlinný tvar, potřebujeme dvě věci: umět zacházet s L-systémy a umět se dívat, abychom zachytili pravidla utváření rostlinného těla. Jde-li nám pouze o to, jak rostlina vypadá, nemusíme vědět, jak se vyvíjí. Modely stromů nerostou od vzrostných vrcholů na špičce větviček, ale sestavují se z předem vypočítaných modulů jako stavebnice.To, že o mechanizmu vývoje nemusíme vědět téměř nic, je možná pro rozvoj „modelovací“ technologie štěstím. Kdybychom k vytvoření modelu borovice potřebovali znát osudy každé molekuly v každé buňce jejích jehlic, daleko bychom se nedostali – a výrobce animovaných filmů a počítačových her by ani nenapadlo podporovat vývoj technik počítačového modelování. Pro biologickou interpretaci modelů je to však nevýhodou: mohou vůbec pomoci přírodozpytnému pochopení vývoje rostlin, jestliže lze sestrojit správný model i na základě chybných předpokladů?
Naštěstí to neznamená, že ze správných předpokladů správný model sestrojit nelze. Očekáváme-li od modelu víc než hezký obrázek (například test hypotézy o šíření morfogenetických signálů rostlinou), musíme navíc požadovat, aby předpoklady byly biologicky reálné – např. aby se signály šířily pouze po již existujících strukturách a ne po větvích, které dosud nevyrostly. Modely pak mohou pomoci odpovědět na fyziologické otázky.
Můžeme si to ukázat na příkladu modelování prostorového uspořádání květenství nenápadného plevele mléčky zední (Mycelis muralis), rostliny příbuzné salátu. Květenství mléčky je bohatě větvená lata s nejstaršími úbory na vrcholu a nejmladšími na spodních postranních osách. Úbory tedy rozkvétají od vrcholu (laty i každé postranní osy) a postranní osy uprostřed květenství jsou větvené bohatěji než ty níže i výše položené. Jedna z konvenčních představ mechanizmu vzniku takového uspořádání je znázorněna na obrázku. Tuto představu lze formalizovat v podobě L-systému, avšak model založený pouze na konvenčních předpokladech neodpovídá skutečnosti. Abychom dostali realistický obraz vývoje laty, potřebujeme kromě signálů zajišťujících indukci květních pupenů a „odblokování“ růstu postranních větví ještě další předpoklady, jejichž potřeba by bez modelu nebyla zřejmá.
 Tyto předpoklady mohou mít několik podob. Míra „zablokování“ postranních větví může záviset na jejich vzdálenosti od vrcholu, takže větve blízké vrcholu se nemohou rozvíjet tak košatě jako ty vzdálenější; ale můžeme si také představit, že zároveň s odblokováním každé větve vychází z její báze signál indukující kvetení podobně, jako tomu bylo u hlavní lodyhy. Do modelu lze vtělit obě představy; a ačkoli odpovídající L-systém vypadá pokaždé jinak, výsledná „virtuální mléčka“ se v žádném vývojovém stadiu neliší! Narazili jsme na hranici možností modelu: abychom rozhodli, který z předpokladů je správný, musíme se vrátit do laboratoře – ale model aspoň naznačuje, co bychom měli hledat.
Tyto předpoklady mohou mít několik podob. Míra „zablokování“ postranních větví může záviset na jejich vzdálenosti od vrcholu, takže větve blízké vrcholu se nemohou rozvíjet tak košatě jako ty vzdálenější; ale můžeme si také představit, že zároveň s odblokováním každé větve vychází z její báze signál indukující kvetení podobně, jako tomu bylo u hlavní lodyhy. Do modelu lze vtělit obě představy; a ačkoli odpovídající L-systém vypadá pokaždé jinak, výsledná „virtuální mléčka“ se v žádném vývojovém stadiu neliší! Narazili jsme na hranici možností modelu: abychom rozhodli, který z předpokladů je správný, musíme se vrátit do laboratoře – ale model aspoň naznačuje, co bychom měli hledat.
Ke kolika cílům vede cesta
Ověřování fyziologických hypotéz je jen okrajovou oblastí využití „virtuálních rostlin“. Většinou jde o výrobu co možná věrohodných obrázků, nejen pro potěšení těch, kdo si hrají s virtuální realitou. Prostorové modely rostlin mohou být užitečné při odhadu chování makroskopických vlastností celých porostů (například odrazu světla, využití sluneční energie či odpařování vody). Dobrý model porostu pšenice či bavlníku sice nenahradí polní pokusy, ale může pomoci při návrhu skutečného experimentu tak, abychom se z jeho výsledků dověděli co nejvíc.Kromě vcelku samozřejmých a od samého počátku zamýšlených výstupů ale matematické modely rostlin otevírají pole možností, které možná potěší oko přírodopiscovo, avšak přírodozpytce přivádějí spíš do rozpaků.
Číselné parametry L-systémů, na jejichž základě rostlinné tvary modelujeme, nejsou omezené na empiricky zjištěné hodnoty. Zkoumáme-li prostor možných hodnot parametrů, zjistíme, že tentýž L-systém s různými hodnotami parametrů může generovat stejně dobře abstraktní, nepřirozené struktury, jako snadno rozpoznatelné rostlinné tvary od listu kapradiny až po siluetu lípy (obrázek).
Zvykli jsme si na představu, že kapradina i lípa se vyvíjejí z jediné buňky posloupností fyziologických dějů, podmíněných souhrou činnosti nejrůznějších genů. Příliš nás neudivuje, že geny kapradiny a lípy jsou si navzájem mnohem podobnější než zmíněné dvě rostliny. Rozdíl je asi spíš záležitostí různých pravidel regulace genové aktivity než důsledkem pozvolného nahromadění bodových mutací. Současná biologie je do značné míry soustředěna právě na vyhledávání rozdílů, na nichž záleží. Doufáme, že studium genomů a ontogeneze modelových organizmů pomůže rekonstruovat klíčové evoluční události, které daly vzniknout rozmanitým tělním plánům, s nimiž se v současném světě setkáváme; že se tak – snad – opět setká vývojová mechanika se zkoumáním rozmanitosti, přírodopis s přírodozpytem. Co si ale v rámci téže biologie počít se zjištěním, že tvarové rozdíly mezi lípou a kapradinou lze lépe než metodami molekulární fyziologie zachytit prostou změnou několika formálních parametrů L-systému – parametrů, které by nám bylo zatěžko reifikovat?
Život jako obraz a příběh aneb O výhodách binokulárního vidění
Pokud nechceme zůstat u wilsonovských pochybností o smyslu modelovacího úsilí, máme přinejmenším dvě možnosti.První je rezignace. Můžeme se smířit s tím, že molekulární a fyziologický pohled na morfogenezi je něco jiného než hra s formálními modely. Máme před sebou dva různé průměty mnohorozměrné skutečnosti na dvě vzájemně kolmé roviny. Ani jeden nevypovídá nic o druhém, nepřispívá k němu, ale také mu nepřekáží. Na svět hledíme buď okem přírodopisným, nebo přírodozpytným. Buď se zabýváme tvary (a stačí nám formální parametry), nebo mechanizmy (a trváme na reifikaci modelů). Obojí můžeme zkoumat a popisovat náležitými metodami, ale nemůžeme čekat, že se dva alternativní popisy smysluplně setkají.
A přece: není příklad s modelováním květenství mléčky dokladem, že k takovému setkání došlo? Věřím, že ano; a nejen to. Dobře se na něm dá ukázat, jak obezřetně se musíme stavět k reifikaci formálních parametrů. Morfogenezi můžeme modelovat více způsoby, a vždycky při tom lze vymyslet fyziologickou reifikaci. Jenže všechny možnosti zároveň platit nemohou: kromě reifikací vysloveně špatných (například že stačí pouhé dva signály) máme už jen takové, u nichž nelze bez dalšího rozlišit, zda jsou, či nejsou správné. A to není jen zvláštnost matematického modelování tvarů. Ani reifikace Monodova modelu růstu bakteriální kultury není bez problémů. Pro opravdové mikroby je přechod do stacionární fáze aktivním, řízeným rozhodnutím, nikoli prostým důsledkem limitace jediného metabolického enzymu. Můžeme předpokládat, že mikrobi mají na povrchu buněk receptory pro nějakou kritickou živinu, které se formálně chovají jako Monodův limitující enzym; ale to v původním modelu nebylo. Trochu cynicky bychom mohli shrnout, že úspěšně reifikovaný model mívá blíž k etiologickému mýtu – vyprávění o tom, co si myslíme o původu modelovaného jevu – než k popisu skutečnosti, že „fyziologický“ model není o nic lepší než model abstraktní a že na tom, že parametry modelu nelze reifikovat, není nic špatného.
Ale je tu i druhá možnost. Můžeme se ptát, jaký je vztah mezi formálními parametry a experimentálně zachytitelnou fyziologií. Můžeme místo konstrukce modelů „zdola“, od představy o mechanizmu, usilovat o dodatečnou reifikaci formálních parametrů. Generuje-li formální model jednou list kapradiny a podruhé lípu, je na místě ptát se, jaké fyziologické děje by se mohly skrývat za jeho parametry. Nedaly by se tyto parametry odvodit z toho, co víme o regulaci zakládání orgánů, vlivu fytohormonů na tento proces, či vlivu různé citlivosti rostlinných orgánů k fytohormonům? Lze do modelu vnést fyzikální vlastnosti rostlinného těla?
Máme na vybranou. Můžeme modelům vytýkat jejich neschopnost postihnout známé molekulární mechanizmy – anebo v nich spatřovat nedokonalé, leč užitečné nástroje k uchopení jevů, o kterých toho pořád ještě víme velice málo. Můžeme přírodu rozdělit pečlivě hlídanou demarkační čárou mezi přírodopisce a přírodozpytce – anebo s radostným očekáváním vstoupit do prostoru netušených možností, který se otvírá na pomezí.
Myslím si, že je jen jeden způsob jak postihnout prostorový tvar výstižněji než průmětem na dvě vzájemně kolmé roviny: pohled oběma očima.
Literatura
P. Prusinkiewicz, A. Lindenmayer: The algorithmic beauty of plants, Springer, New York-Berlin-Heidelberg 1990Marek T. Michalewicz (ed): Plants to ecosystems: advances in computational life sciences, CSIRO, Colingwood (Australia) 1997
Citát
Przemysl Prusinkiewicz a Aristid Lindenmayer: The algorithmic beauty of plants, s. 175
Používání přibližných obrazů k ilustraci abstraktních představ má dlouhou tradici v geometrii. Vždyť ani základní prvky euklidovské geometrie – bod a přímku – nelze přesně nakreslit. Zajímavá však je otázka vztahu mezi fraktály a skutečnými biologickými strukturami. Ty se totiž skládají z konečného počtu buněk, a proto nemohou být fraktály v pravém smyslu toho slova. Skutečné rostliny bychom mohli pokládat za aproximace „dokonalých“ struktur fraktálů jen tehdy, kdybychom přijali Platonovu představu idejí nadřazených jejich pozemskému ztělesnění. Nadějnější však je opačný přístup: fraktály můžeme pokládat za abstraktní popis skutečných struktur, i když se to na první pohled může zdát podivné.
Matematické modely růstové křivky mikroorganizmů
Chování mikrobiální populace za reprodukovatelných (byť i ne právě přirozených) laboratorních podmínek lze předvídat. Zaočkujeme-li malé množství výchozí kultury do dobře míchané tekuté živné půdy, chvíli se neděje nic (mikrobi si zvykají na změnu prostředí), a pak kultura čile začne exponenciálně růst. Po určité době buňky růst opět zvolní, a posléze zastaví, zpravidla proto, že spotřebovaly živiny nebo si otrávily prostředí produkty vlastního metabolizmu.
Chceme-li matematicky modelovat vývoj kultury, musíme najít funkci, která vyjadřuje závislost koncentrace buněk v živné půdě N na čase t. Jednou z možností je funkce popisující tvar logistické křivky, kterou často používají ekologové při popisu vývoje velikosti populací podstatně větších organizmů v prostředí, v němž nelze oddělit jednotlivé vlivy přispívající k omezení rychlosti růstu. Její odvození vychází z předpokladu, že rychlost růstu populace (dN/dt) lineárně klesá s její rostoucí hustotou N dle rovnice dN/dt = r . N, přičemž r = r0 (1-N/K), kde parametr r0 postihuje maximální možnou rychlost růstu za optimálních podmínek. K je obtížně interpretovatelný formální parametr, který nějak závisí na konkurenci uvnitř populace, ale nic nevypovídá o povaze této konkurence: byl zvolen tak, aby závislost mezi hustotou populace a růstovou rychlostí byla co nejjednodušší to jest lineární.
Jinak je tomu u častěji používaného modelu, který zavedl Jacques Monod. Monodův model vychází ze dvou předpokladů: kultura roste exponenciálně, tedy N = N0 . eμt, a specifická růstová rychlost μ závisí na koncentraci S právě jedné živiny (substrátu) v prostředí totiž té, jejíž nedostatek limituje růst kultury. Předpokládáme-li dále, že tato limitace se odehrává na úrovni jediné enzymové reakce, jejíž kinetika odpovídá reakci neregulovaného enzymu se substrátem, lze odvodit, že μ = μmax . S/(Ks + S), kde μmax odpovídá maximální dosažitelné růstové rychlosti a Ks vyjadřuje míru afinity limitujícího substrátu k příslušnému enzymu.
Navzdory odlišné matematické formalizaci lze z logistického i Monodova modelu odvodit podobné křivky, a bylo by obtížné na základě experimentálních výsledků rozhodnout, který model je lepší. Rozdíl nespočívá v kvalitě predikce dat, ale v tom, že parametrům Monodova modelu lze přisoudit fyziologický význam.
L-systémy
Jeden z teoretických rámců pro modelování biologických struktur (ne nutně rostlinných) představují L-systémy. Písmeno L připomíná profesora Aristida Lindenmayera (19251989), který r. 1968 formuloval základy této teorie.
Modelování vychází z předpokladu, že organizmus lze rozdělit na větší počet jednotek modulů. Mohou to být jednotlivá internodia, orgány, nebo i jednotlivé buňky. Osudy modulů lze předvídat květní pupen dá vzniknout poupěti, poupě květu a květ plodu. Vzájemné přeměny modulů můžeme formálně zachytit v podobě odvozovacích pravidel (productions). Předpokládáme nyní, že sledujeme osudy nějaké výchozí struktury (označované jako axiom), jejíž vývoj pozorujeme v nespojitém čase: mezi každými dvěma okamžiky pozorování se struktura promění tak, že všechny její moduly nahradí moduly předepsané odvozovacími pravidly. Uvedený příklad bychom mohli popsat takto:
axiom: květní pupen
pravidlo 1: květní pupen → poupě
pravidlo 2: poupě → květ
pravidlo 3: květ → plod
Úlohu modulů nemusejí hrát jen skutečné objekty. V následujícím příkladu je třeba k psaným pravidlům přičinit ještě jedno nepsané: symbol, jehož proměnu nepopisuje žádné pravidlo, se nemění.
axiom: X
pravidlo 1: X → F[+X][-X]FX
pravidlo 2: F → FF
Dostaneme tedy v sérii po sobě jdoucích kroků posloupnost:
X F[+X][-X]FX FF[+F[+X][-X]FX][- F[+X][-X]FX]FFX ...
Každému znaku (modulu) posloupnosti můžeme přiřadit předem zvolený geometrický smysl. Lindenmayerův žák Przemysl Prusinkiewicz zavedl metodu interpretace symbolů želvou (turtle interpretation of symbols). Každé písmeno při ní vykládáme jako příkaz pomyslné želvičce, která putuje rovinou či prostorem a při tom kreslí. (V praxi želvičku představuje program, který musí být opět interpretován a vposledku převeden na řadu nul a jedniček strojového kódu.)
V našem případě při konvenční notaci F znamená nakresli úsečku jednotkové délky, + otoč se o daný úhel doprava, otoč se o tentýž úhel doleva a hranatá závorka udělej, co je v závorce, a vrať se bez kreslení na její začátek. Písmenu X želvička nerozumí a ignoruje je. Při vhodně zvoleném úhlu po několika krocích dostaneme strukturu, která připomíná list okoličnaté byliny (obrázek). Navíc má ještě jednu zajímavou vlastnost: při vyšším počtu kroků zřetelně vyvstává soběpodobnost výsledného tvaru při nekonečně mnoha krocích bychom dostali fraktál.
Uvedený příklad představuje jeden z nejjednodušších L-systémů, schopných generovat obrazy podobné rostlinám. Víc možností se otevře, pokud želvičku obdaříme schopností pohybu v prostoru. Krom toho se objekty nemusejí skládat pouze z úseček: jejich součástí mohou být i další objekty (třeba listy a květy) a ty můžeme definovat buďto od oka (třeba i zprůměrováním změřených prostorových tvarů skutečných listů), nebo zase pomocí L-systémů.
Když místo předem daných úhlů a jednotkových kroků želvičky zavedeme možnost definovat úhly a vzdálenosti reálnými čísly parametry, které mohou být určeny matematickými funkcemi, můžeme do modelu zavést třeba závislost růstové rychlosti lodyhy na jejím stáří. Nahodilé vlivy můžeme modelovat za pomoci generátoru náhodných čísel, který ovlivňuje parametry nebo i podobu odvozovacích pravidel (například tím, že pro nějaký modul vybírá z více osudů s různou pravděpodobností pupen může vyrašit, zůstat v klidu nebo zahynout).
Z biologického hlediska ještě zajímavější důsledky má zavedení závislosti odvozovacích pravidel na kontextu poloze modulu v rámci struktury. Umožňuje modelovat i takové děje, jako je šíření signálních molekul rostlinou a odpověď jednotlivých orgánů na signály. Dokonce lze sestrojit i L-systémy, které se vyvíjejí ve spojitém čase.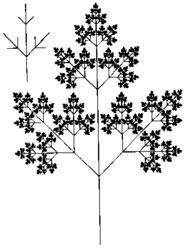
Ke stažení
 Článek ve formátu PDF [555,37 kB]
Článek ve formátu PDF [555,37 kB]
O autorovi
Fatima Cvrčková





















